【Python】闭包与装饰器

article/2025/8/27 20:28:34

1.闭包

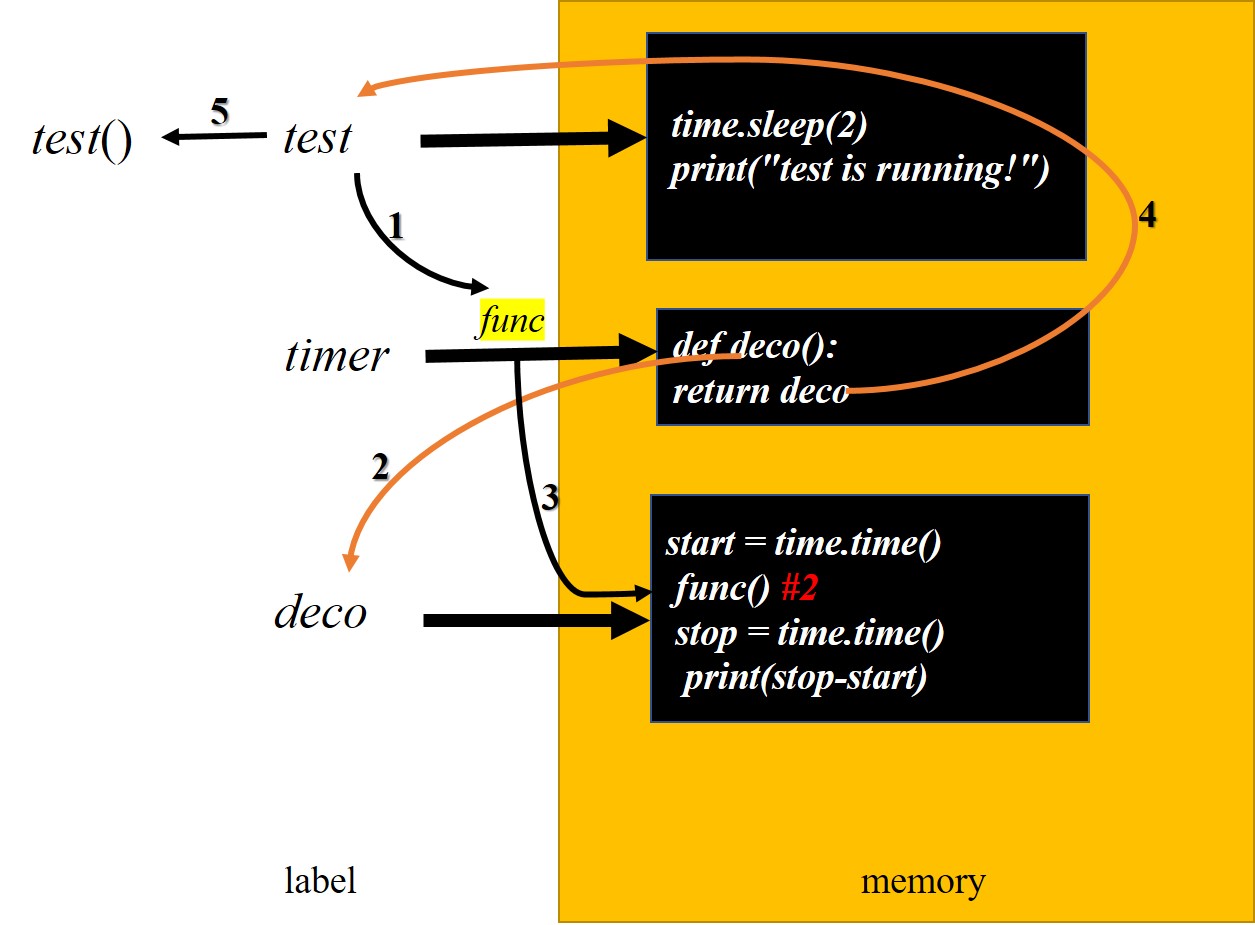
闭包的本质就是函数的嵌套定义，即在函数内部再定义函数

闭包有两种不同的方式，第一种是“返回一个函数名称”，第二种是在函数内部就“直接调用”

闭包的定义：在一个外函数中定义了一个内函数，内函数里运用了外函数的临时变量，并且外函数的返回值是内函数的引用

引用是什么？Python 中的几乎所有东西都是对象，拥有属性和方法，包括整型，浮点型、函数，都是对象

返回一个函数名称：

# 定义外层函数
def outer():# 外函数临时变量num_01num1 = 100def inner():# 内函数里运用了外函数的临时变量num2 = num1 + 1print("num2 =",num2)# 外函数的返回值是内函数的引用return inner   outer()()  # print为：num2=101

outer外函数返回内函数 inner的引用

直接调用：

def outer():# 外函数临时变量num1num1 = 100def inner():# 内函数里运用了外函数的临时变量num2 = num1 + 1print("num2 =",num2)# 外函数的返回值是内函数的引用return inner()   outer()# print为：num2=101

闭包的优缺点

优点

可以避免使用全局变量，防止全局变量污染
可以读取函数内部的变量
延长了局部变量的作用域范围

缺点

变量不会被收回，消耗内存
会造成内存泄漏

2.装饰器

采用了闭包的思路，在不改变原函数功能的情况下，为函数增添新的功能

装饰器的语法以@开头，接着是装饰器函数的名字和可选的参数。紧跟着装饰器声明的是被修饰的函数和装饰函数的可选参数

装饰器的应用场景：引入日志、函数执行时间统计、执行函数前预备处理、执行函数后清理功能、权限校验等场景、缓存、事务处理、数据清理、数据添加、附加功能等

格式：

# 外层函数
def outer(func):# 内层函数def inner():func()# 额外添加的功能print("hello")# 外层函数返回内层函数的引用return inner@outer   # 给gat函数添加 outer装饰器
def gat():passgat()# print为>> hello

装饰器作用：在不改变函数原有代码的基础上，添加额外的功能

参数传递

1.装饰器形式

def outer(func):def inner():print("装饰器开始执行")print("功能添加")func()print("装饰器结束执行")return inner@outer   # 给add函数添加 outer装饰器
def add():print("hello")add()# print为>> 装饰器开始执行
#           功能添加
#           hello
#           装饰器结束执行

2.装饰器传参形式

def outer(func):def inner(a, b):print("装饰器执行")print("A---B")func(a, b)print("装饰器结束执行")return inner@outer  # 给add函数添加一个outer装饰器
def add(a, b):print("a+b = ", (a+b))add(10,20)# print为>> 装饰器执行
#           A---B
#           a+b =  30
#           装饰器结束执行

3.不定长参数传参

def outer(func):def inner(*args, **kwargs):print("装饰器执行")print("A---*---B")func(*args, **kwargs)print("装饰器结束执行")return inner@outer  # 给add函数添加一个outer装饰器
def add(a, b，c，d):print("a+b+c+d = ", (a+b+c+d))add(10, 20, 30, 40)# print为>> 装饰器执行
#           A---*---B
#           a+b+c+d =  100
#           装饰器结束执行

类装饰器

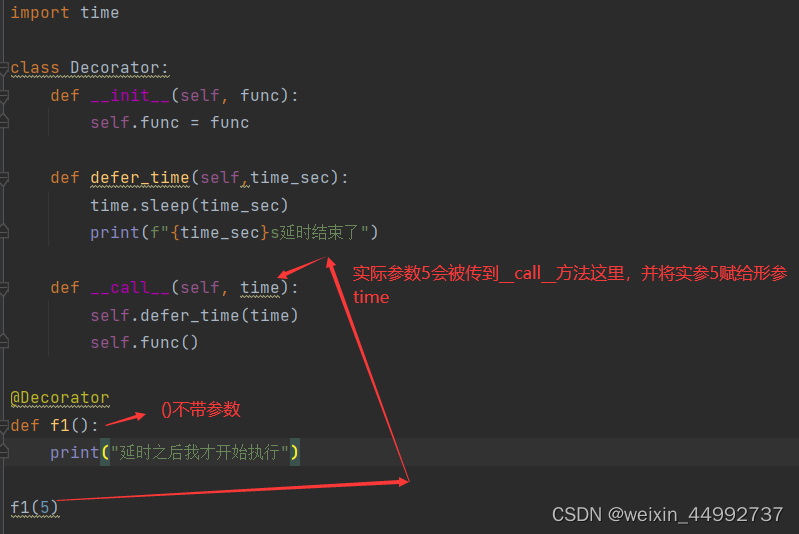
使用类来实现装饰器的功能的，称之为类装饰器。类装饰器的实现是调用了类里面的__call__函数

类作为一个装饰器时：

通过__init__（）初始化类
通过__call__（）调用真正的装饰方法

class ClsDecorator:def __init__(self, func):self.func = funcprint("执行类的__init__方法")def __call__(self, *args, **kwargs):print('__call__函数')self.func(*args, **kwargs)print("<call>函数")@ClsDecorator
def outer1():print("函数>>outer1")def outer():print("未使用类装饰器")@ClsDecorator
def outer2(name):print('函数》》outer2')name()print("倒数第二次执行")if __name__ == '__main__':outer1()outer2(outer)

打印结果：

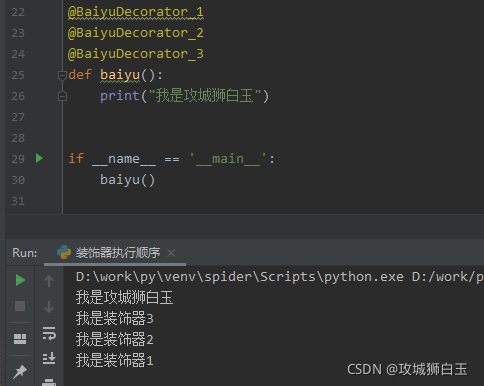
多层装饰器

def outer1(func):def inner(*args,**kwargs):print("装饰器1执行")print("A-----B")func(*args,**kwargs)print("装饰器1结束执行")return innerdef outer2(func):def inner(*args,**kwargs):print("装饰器2执行")print("C-----D")func(*args,**kwargs)print("装饰器2结束执行")return inner@outer1  # 给outers函数添加一个outer1装饰器
@outer2  # 给outers函数添加一个outer2装饰器
def outers(a, b，c，d):print("a+b+c+d = ", (a+b+c+d))outers(10, 20, 30, 40)# 运行结果 / 执行顺序
装饰器1执行
A-----B
装饰器2执行
C-----D
a+b+c+d = 100
装饰器2结束执行
装饰器1结束执行

多层装饰器开始执行时，自上而下开始执行装饰器功能，当执行完执行函数中的操作之后，自下而上的结束装饰器执行

常用内置装饰器

1.@staticmethod: 静态方法，没有和类本身有关的参数，无需实例化，直接通过类.方法名调用，也可以通过实例.方法名调用

2.@property：使调用类中的方法像引用类中的字段属性一样。被修饰的特性方法，内部可以实现处理逻辑，但对外提供统一的调用方式

3.@classmethod: 与staticmethod很相似，第一个参数需要是表示自身类的 cls 参数，可以来调用类的属性，类的方法，实例化对象

装饰器的优缺点

优点