微分方程数值解法（2）——椭圆型方程的有限差分法

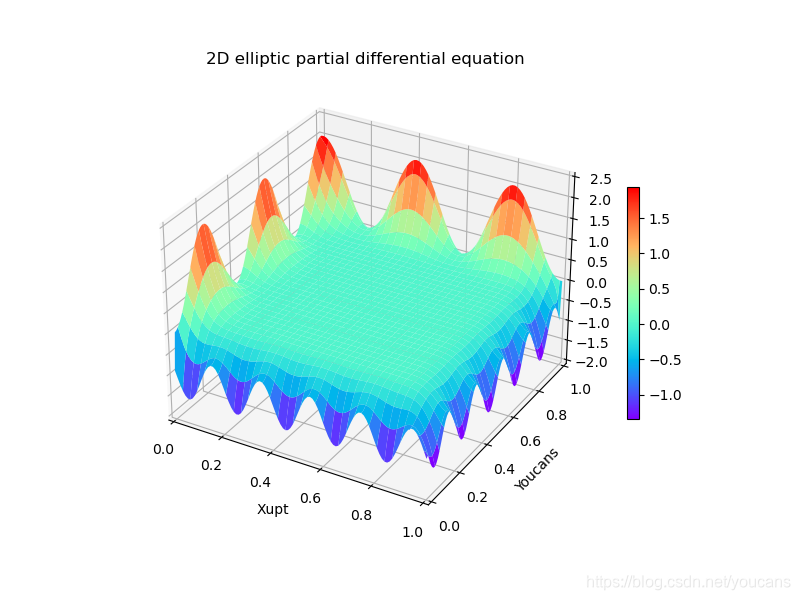
此处参考教材为李荣华的《微分方程数值解法》
使用工具：Matlab

1. 算法：矩形网格上5点差分格式

在这里插入图片描述

2. 算法

I.需要求解的函数

function [v,vx,vy,f,aa,bb,cc,dd]=u2D(x,y,ft)% ft为方程编号，u1D为精确解函数u（t）,注意与f2D 对应右端项函数f(t,u(t))switch ftcase 1 %P-104例题v=cos(3*x).*sin(pi*y)/(9+pi^2);vx=-3*sin(3*x).*sin(pi*y)/(9+pi^2);vy=pi*cos(3*x).*cos(pi*y)/(9+pi^2);f=cos(3*x).*sin(pi*y);aa=0;bb=pi;cc=0;dd=1;case 2 %P-104习题v=exp(pi*(x+y)).*sin(pi*x).*sin(pi*y);
vx=pi*exp(pi*(x+y)).*(sin(pi*x).*sin(pi.*y)+cos(pi*x).*sin(pi*y));
vy=pi*exp(pi*(x+y)).*(sin(pi*x).*sin(pi*y)+cos(pi*y).*sin(pi*x));
f=-2*(pi^2)*exp(pi*(x+y)).*(sin(pi*x).*cos(pi*y)+cos(pi*x).*sin(pi*y));
aa=0;bb=1;cc=0;dd=1;
end

II.求解例题的主函数：五点差分格式函数

function Elliptic_PDESolver(ft,M,N)
%初始化定义求解区域和网格
[~,~,~,~,x1,xr,y1,yr]=u2D(0,0,ft); %求解区域也从u2D函数调用，初始x和y设为0
h1=(xr-x1)/M;
h2=(yr-y1)/N;
xd=(x1:h1:xr); %网格节点坐标
yd=(y1:h2:yr); %网格节点坐标%定义全部节点编号集AId，网格节点编号与矩阵下标编号不一致
AId=zeros(M+1,N+1);
xk=zeros((M+1)*(N+1),1); %整体编号排序后的节点坐标
yk=zeros((M+1)*(N+1),1); %整体编号排序后的节点坐标
for i=0:Mfor j=0:NAId(i+1,j+1)=i*(N+1)+j+1; %注意矩阵编号从1开始，故i+1，j+1xk(i*(N+1)+j+1)=xd(i+1); %xd的编号从1开始，故i+1yk(i*(N+1)+j+1)=yd(j+1); %yd的编号从1开始，故j+1end
end
AId=AId';AId=AId(:);%定义内部节点编号集：InId
InId=zeros(M-1,N-1);
for i=1:M-1for j=1:N-1InId(i,j)=i*(N+1)+j+1;end
end
InId=InId';InId=InId(:);%定义左边界节点编号集   LbId
for j=0:NLbId(j+1)=0*(N+1)+j+1;
end%定义右边界节点编号集   RbId
for j=0:NRbId(j+1)=M*(N+1)+j+1;
end%定义下边界节点编号集  　BbId
for i=0:MBbId(i+1)=i*(N+1)+0+1;
end%定义上边界节点编号集  　TbId
for i=0:MTbId(i+1)=i*(N+1)+N+1;
end%显示整体节点编号图
figure;
for i=0:Mplot(xd(i+1)+0*yd,yd);hold on;
end
for j=0:Nplot(xd,yd(j+1)+0*xd);hold on;
end
for i=1:length(AId)text(xk(i),yk(i),num2str(i));
end%初始化矩阵右端项
A=zeros((M+1)*(N+1),(M+1)*(N+1));
b=zeros((M+1)*(N+1),1);
hh1=h1^2;
hh2=h2^2;%内部节点形成矩阵行元素及右端项
for i=1:length(InId)k=InId(i);A(k,k)=2*hh1+2*hh2;A(k,k-1)=-hh1;A(k,k+1)=-hh1;    A(k,k-N-1)=-hh2;A(k,k+N+1)=-hh2;[~,~,~,ff]=u2D(xk(k),yk(k),ft); %提取右端项函数值b(k)=hh1*hh2*ff;
end
%添加边界条件元素及右端项
%定义左边界节点矩阵行元素及右端项
for j=1:length(LbId)
k=LbId(j);
if ft==1A(k,k)=-1;A(k,k+N+1)=1;
[~,ux,~,~]=u2D(xk(k),yk(k),ft); %%提取右端项函数值，第二边值条件b(k)=h1*ux;
elseif ft==2A(k,k)=1;A(k,k+N+1)=0;[uv,~,~,~]=u2D(xk(k),yk(k),ft);  %提取右端项函数值;第一边值条件b(k)=uv;%b(k)=0;end
end% 定义右边界节点矩阵行元素及右端项
for j=1:length(RbId)
k=RbId(j);if ft==1A(k,k)=-1;A(k,k-N-1)=1;
[~,ux,~,~]=u2D(xk(k),yk(k),ft); %提取右端项函数数值，第二边值条件b(k)=h1*ux;elseif ft==2A(k,k)=1;A(k,k-N-1)=0;[uv,~,~,~]=u2D(xk(k),yk(k),ft);  %提取右端项函数数值，第一边值条件b(k)=uv;%b(k)=0;end
end% 定义下边界节点矩阵行元素及右端项
for i=1:length(BbId)k=BbId(i);A(k,:)=0; %由于与其他边界条件有重复，清空该行元素A(k,k)=1;[uv,~,~,~]=u2D(xk(k),yk(k),ft); %提取右端项函数值，第一边值条件b(k)=uv;%b(k)=0;
end% 定义上边界节点矩阵行元素及右端项
for i=1:length(TbId)k=TbId(i);A(k,:)=0; %由于与其他边界条件有重复，清空该行元素A(k,k)=1;[uv,~,~,~]=u2D(xk(k),yk(k),1); %提取右端项函数值，第一边值条件b(k)=uv;%b(k)=0;
enduk=A\b; %求解所得整体节点排序的数值解
ExUk=u2D(xk,yk,ft); %所得整体节点排序的精确解
MaxErr=max(abs(uk-ExUk));
fprintf('MaxErr=%3.6f\n',MaxErr);%将数值解转化为网格排序
NuU=zeros(M+1,N+1);
for i=0:Mfor j=0:Nk=i*(N+1)+j+1;NuU(i+1,j+1)=uk(k);end
end
NuU=NuU'; %转置后矩阵下标与U相同%精确解画图
[X,Y]=meshgrid(xd,yd);
U=u2D(X,Y,ft);
figure;
mesh(X,Y,U);
xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis');
hold on;
%数值解画图
plot3(xk,yk,uk,'+');
hold on;

III.补充算例：八边形区域剖分

function Elliptic_PDESolver2(ft,M,N)
fprintf('八边形区域网格剖分数M和N需相等并且为3的倍数 \n');
if(M~=N)||(mod(M,3)~=0)fprintf('输入M和N不正确 \n');return
end%clear all
% 初始化定义求解区域和网格
%ft=1;
%M=18;%N=18;[~,~,~,~,x1,xr,y1,yr]=u2D(0,0,ft); %求解区域也从u2D函数调用，初始x和y设为0
h1=(xr-x1)/M;
h2=(yr-y1)/N;
xd=(x1:h1:xr); %网格节点坐标
yd=(y1:h2:yr); %网格节点坐标% 定义全部节点编号集 AId，注意网格节点编号与矩阵下标编号
AId=zeros(M+1,N+1);
xk=zeros((M+1)*(N+1),1); %整体排序后的节点坐标
yk=zeros((M+1)*(N+1),1); %整体排序后的节点坐标
for i=0:Mfor j=0:NAId(i+1,j+1)=i*(N+1)+j+1; %注意矩阵编号从1开始，故i+1，j+1xk(i*(N+1)+j+1)=xd(i+1); %xd的编号从1开始，故i+1yk(i*(N+1)+j+1)=yd(j+1); %yd的编号从1开始，故i+1end
end
AId=AId';AId=AId(:);%显示整体节点编号图
figure;
for i=0:Mplot(xd(i+1)+0*yd,yd,'-.');hold on;
end
for j=0:Nplot(xd,yd(j+1)+0*xd,'-.');hold on;
end
for i=1:length(AId)text(xk(i),yk(i),num2str(i));
end%八边形区域
%定义内部节点编号集 InId
InId=[]; 
B1Id=[]; %四条斜边
B2Id=[]; %左边
B3Id=[]; %右边
B4Id=[]; %下边
B5Id=[]; %上边
for i=0:Mfor j=0:Nif(i>0)&&(i<M)&&(j>0)&&(j<N)&&(j>N/3-i)&&(j<2*N/3+i)&&(j>i-2*N/3)&&(j<5*N/3-i)InId=[InId,i*(N+1)+j+1];endif(j==N/3-i)||(j==2*N/3+i)||(j==i-2*N/3)||(j==5*N/3-i)B1Id=[B1Id,i*(N+1)+j+1];endif(i==0)&&(j>N/3)&&(j<2*N/3)B2Id=[B2Id,i*(N+1)+j+1];endif(i==M)&&(j>N/3)&&(j<2*N/3)B3Id=[B3Id,i*(N+1)+j+1];endif(j==0)&&(i>M/3)&&(i<2*M/3)B4Id=[B4Id,i*(N+1)+j+1];endif(j==N)&&(i>M/3)&&(i<2*M/3)B5Id=[B5Id,i*(N+1)+j+1];endend
end
plot(xk(InId),yk(InId),'ro');
hold on;
plot(xk(B1Id),yk(B1Id),'b*');
hold on;
plot(xk(B2Id),yk(B2Id),'g*',xk(B3Id),yk(B3Id),'g*');
hold on;
plot(xk(B4Id),yk(B4Id),'c*',xk(B5Id),yk(B5Id),'c*');
hold on;% 初始化矩阵和右端项
A=zeros((M+1)*(N+1),(M+1)*(N+1));
b=zeros((M+1)*(N+1),1);
hh1=h1^2;
hh2=h2^2;%内部节点形成矩阵行元素及右端项
for i=1:length(InId)k=InId(i); %提取内部节点编号A(k,k)=2*hh1+2*hh2;A(k,k-1)=-hh1;A(k,k+1)=-hh1;    A(k,k-N-1)=-hh2;A(k,k+N+1)=-hh2;[~,~,~,ff]=u2D(xk(k),yk(k),1); %提取右端项函数数值b(k)=hh1*hh2*ff;%b(k)=hh1*hh2*(cos(3*xk(k))*sin(pi*yk(k)));
end%添加边界条件矩阵元素及右端项
% 定义B1Id边界节点矩阵行元素及右端项
for j=1:length(B1Id)k=B1Id(j);A(k,k)=1;[uv,~,~,~]=u2D(xk(k),yk(k),1); %提取右端项函数数值,第一边值条件b(k)=uv;
end% 定义B2Id边界节点矩阵行元素及右端项
for j=1:length(B2Id)k=B2Id(j);A(k,k)=-1;A(k,k+N+1)=1;[~,ux,~,~]=u2D(xk(k),yk(k),1); %提取右端项函数数值，第二边值条件b(k)=h1*ux;
end% 定义B3Id边界节点矩阵行元素及右端项
for j=1:length(B3Id)k=B3Id(j);A(k,k)=1;A(k,k-N-1)=-1;[~,ux,~,~]=u2D(xk(k),yk(k),1); %提取右端项函数数值，第二边值条件b(k)=h1*ux;
end% 定义B4Id边界节点矩阵行元素及右端项
for j=1:length(B4Id)k=B4Id(j);A(k,k)=-1;A(k,k+1)=1;[~,~,uy,~]=u2D(xk(k),yk(k),1); %提取右端项函数数值，第一边值条件b(k)=h2*uy;
end% 定义B5Id边界节点矩阵行元素及右端项
for j=1:length(B5Id)k=B5Id(j);A(k,k)=1;A(k,k-1)=-1;[~,~,uy,~]=u2D(xk(k),yk(k),1); %提取右端项函数数值，第一边值条件b(k)=h2*uy;
end%矩阵A是按照所有(M+1)*(N+1)个节点生成的矩阵，里面有很多的非区域节点编号对应的0子阵
DmId=sort([InId,B1Id,B2Id,B3Id,B4Id,B5Id]);
OutId=setdiff(AId,DmId);
A(OutId,:)=[];A(:,OutId)=[]; %剔除非区域节点OutId对应的行和列
b(OutId,:)=[]; %剔除非区域节点OutId对应的右端项
uk=A\b; %求解所得整体节点排序的数值解
ExUk=u2D(xk(DmId),yk(DmId),ft); %整体节点排序的精确解
MaxErr=max(abs(uk-ExUk));
fprintf('MaxErr=%3.6f\n',MaxErr);%精确解画图
[X,Y]=meshgrid(xd,yd);
U=u2D(X,Y,ft);
figure;
mesh(X,Y,U);
xlabel('X-axis'),ylabel('Y-axis'),zlabel('Z-axis');
hold on;
%数值解画图
plot3(xk(DmId),yk(DmId),uk,'+');
hold on;