一、 一维椭圆方程数值解


matlab代码:`
function chap2_fdm_elliptic_1D
% 一维椭圆方程求解(常微分方程边值问题)
% -u'' + q(x)u = f(x), 0<x<1, 取q(x) = x, f(x) = (x-1)exp(x)
% u(0) = 1, u(1) = e; 边界条件
% 真解为 u = exp(x)N = 20;
h = 1/N;
x_all = (0:h:1)';
x = x_all(2:end-1);% 方程组右端的处理
u0 = 1;
uN = exp(1);
b = f(x);
b(1) = b(1)+u0/h^2;
b(N-1) = b(N-1)+uN/h^2;% 方程组左端矩阵的建立
B = zeros(N,N);
for i = 1:N-1B(i,i) = -2;B(i,i+1) = 1;B(i+1,i) = 1;
end
B = -1/h^2*B(1:N-1,1:N-1);D =zeros(N-1,N-1);
q = q(x);
for i = 1:N-1D(i,i) = q(i);
end
A = B+D;%求解线性方程组(Gauss消去法求解)
u = gauss(A,b);
u_e = u_exact(x_all);figure(1)
plot(x_all,[u0;u;uN],'r*',x_all,u_e,'b');
endfunction y = u_exact(x)
y = exp(x);
endfunction y = q(x)
y = x;
endfunction y = f(x)
y = (x-1).*exp(x);
endfunction x = gauss(A,B)
%消元过程
n = size(A,2);
m = size(B,2);
for i = 1:mb = B(:,i);for k=1:n-1A(k+1:n,k)=A(k+1:n,k)/A(k,k); %算子A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n);b(k+1:n)=b(k+1:n)-b(k)*A(k+1:n,k); end %回代过程U=A;b=b;for j =n:-1:2b(j)=b(j)/U(j,j);b(1:j-1)=b(1:j-1)-b(j)*U(1:j-1,j);endb(1)=b(1)/U(1,1);B(:,i)=b; %这个就是线性方程组的解了
end
x = B;
end
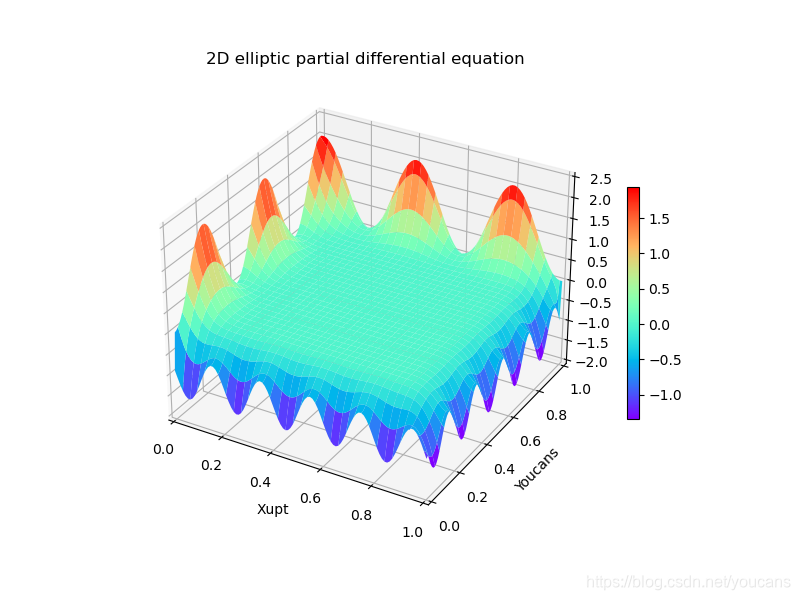
二、二维椭圆型微分方程



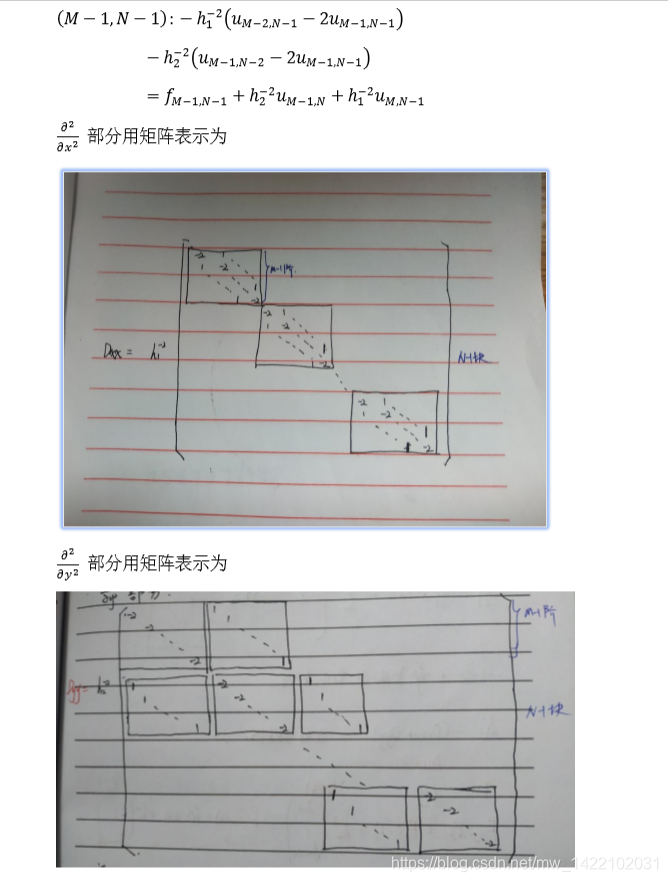


matlab代码:
function chap2_fdm_possion_solution
% 二维的possion方程求解
% -Delta u = -2*exp(x+y) 边界(a,b)*(c,d)
% u(x,0) = exp(x)
% u(x,1) = exp(x+1)
% u(0,y) = exp(y)
% u(1,y) = exp(y+1)
global mLap M_V I hx hya = 0;
b = 1;
c = 0;
d = 1;
M = 40;
N = 30;
hx = (b-a)/M;
hy = (d-c)/N;
x = (a:hx:b)';
y = (c:hy:d)';
[X Y] = meshgrid(x,y);
x_in = (a+hx:hx:b-hx);
y_in = (c+hy:hy:d-hy);
[X_in Y_in] = meshgrid(x_in,y_in);%生成Dxx
d_0 = -2*ones(M-1,1);
d_1 = ones(M-1,1);
d_m1 = d_1;
d_xx = spdiags([d_m1 d_0 d_1],[-1,0,1],M-1,M-1);
d_xx = d_xx/hx^2;
I_N = speye(N-1,N-1);
D_xx = kron(I_N,d_xx);%D_yy
d_0 = -2*ones(N-1,1);
d_1 = ones(N-1,1);
d_m1 = d_1;
d_yy = spdiags([d_m1 d_0 d_1],[-1,0,1],N-1,N-1);
d_yy = d_yy/hy^2;
I_M = speye(M-1,M-1);
D_yy = kron(d_yy,I_M);%左端矩阵
mLap = -(D_xx+D_yy);%右端矩阵
F = f(X_in,Y_in);
F = F';
g_d = g(x_in,0);
g_u = g(x_in,1);
g_l = g(0,y_in);
g_r = g(1,y_in);
F(:,1) = F(:,1)+g_d'/hy^2;
F(:,N-1) = F(:,N-1)+g_u'/hy^2;
F(1,:) = F(1,:)+g_l/hx^2;
F(M-1,:) = F(M-1,:)+g_r/hx^2;%求解u
b = F(:);
u = mLap\b;
U = reshape(u,M-1,N-1);
U = U';%绘制结果
u_e = u_exact(X,Y);
u_num = u_e;
u_num(2:N,2:M) = U;
figure(1)
mesh(X,Y,u_e);
figure(2)
mesh(X,Y,u_num);end%函数
function y = f(x,y)
y = -2*exp(x+y);
endfunction u_e = u_exact(x,y)
u_e = exp(x+y);
endfunction g = g(x,y)
g = exp(x+y);
end