文章目录
- 1.闭包
- 2.不带参数的装饰器
- 3.带参数的装饰器
- 4.不定长参数的装饰器
- 5.多重装饰器修饰
- 6.返回值是装饰器
- 7.装饰器类
Python学习笔记—装饰器
装饰器:从生活角度理解,是对一个东西进行装饰,增加它本身的一些功能和内容;
Python中的装饰器,也大致可以这样理解,它本质上就是扩展原本函数功能的一种函数。它是通过函数闭包进行实现的。
1.闭包
闭包是什么?
答:定义在一个函数中的函数称为闭包函数,前一个函数称为外函数,后一个函数称为内函数,闭包指的就是,内函数总是可以访问其所在的外函数中声明的参数和变量,即使在其外函数被返回之后。
想要实现闭包,需要三个条件:
- 函数嵌套,即存在内函数和外函数
- 内函数使用了外函数的变量或者参数
- 外函数需要return内函数
举例:
def func_out(): # 外函数num1 = 10def func_in(num2): # 内函数t = num1 + num2print("%d + %d = %d"%(num1,num2,t))return func_in # 返回内函数, 不加括号# 这里实际上是 func_out()函数调用之后返回的内函数地址赋值给f
f = func_out()
f(1) # 为了方便记忆,可以直接将内函数与这里的f直接等价,调用的时候,需要以内函数的形参列表为基准传入参数
# 输出: 10 + 1 =11
思考:有没有想过,写在代码中的函数名到底是什么呢?
答:其实是函数体代码的存储地址。
举例:
def test():pass
print(test) # 输出 :<function test at 0x000001AC070275E0>
- 这个时候,在回头看一下闭包的例子,外函数返回的是内函数的地址,f接收的是外函数调用的结束后返回的内函数地址,这时想要调用内函数,直接按照内函数的形参列表给f传入参数即可。
- 在深入一点,一般情况下,在
func_out()函数调用结束后,它内部的num1局部变量理应被销毁释放,但是f在调用时候,还是用到了num1的值,这就是闭包的真正含义。
2.不带参数的装饰器
装饰器就是通过闭包实现的,接下来举两个常见例子帮助理解:
- 日志打印器 – 通知函数执行和结束
def decorate(func): # 这里的参数是函数print("装饰器执行了") # 可以看出,这里的装饰器就是外函数有了参数的闭包def inner():print("执行函数了")func()print("函数执行结束了")return inner;@decorate # @decorate 值得是装饰器语法糖,它的执行意义是 comment = decorate(comment) comment()
def comment():print("评论开始了")comment()
@ 符号就是装饰器的语法糖。它放在一个函数开始定义的地方,它就像一顶帽子一样戴在这个函数的头上,和这个函数绑定在一起。在我们调用这个函数的时候,第一件事并不是执行这个函数,而是将这个函数做为参数传入它头顶上这顶帽子,这顶帽子我们称之为装饰函数 或 装饰器。
- 函数时间计时器 --计算一个函数执行的时间
from time import * # 导入time模块,具体导入模块可以参看我的另一篇文章def decorate(func): # 外函数,这里的func参数为@下一行的函数def inner(): # 内函数begin = time()func() # 这里调用了外函数的局部变量end = time()result = end - begin print("执行的时间为:"+str(result))return inner;@decorate # 装饰器语法糖
def work():s = 0for i in range(1,10001):s += iprint("1到10000的和为%d:"%(s))work()
以上两个例子就是不带参数的装饰器,在写装饰器的时候要注意装饰器内函数中调用func的形式,有时候func(@下一行 的函数)是有return返回值的,需要注意一下。
3.带参数的装饰器
- 带参数的装饰器,指的是装饰器内部inner函数是需要有参数,也表明@装饰器修饰的函数也是需要有和inner函数有相同的形参列表。
举例:
def decorate (func):def inner(a,b): # 这里的inner函数有参数,则也需要func也需要有参数print("努力计算中!!!")func(a,b)return inner@decorate # 这里本质是 f = decorate(add1), f(a,b) 所以inner函数也需要和add1函数有相同的形参列表
def add1(a,b): print("%d + %d = %d"%(a,b,a+b))add1(2,3)
# 输出: 努力计算中!!!
# 2 + 3 = 5
建议想要加深理解,一定要参考上面提到的函数名本质是函数本体代码存放的地址,就是一段地址值。将注释后的代码用地址代入走一遍,就更容易理解了
4.不定长参数的装饰器
有了上面的带参数的装饰器,这里的不定长参数的装饰器,就是将inner函数的参数列表改为不定长参数占位符就可以了。具体可以参考我的另外一篇文章《Python函数中的不定长参数》
举例:
def decorate(func):def inner(*args,**kwargs): # 不定长参数列表print("不定长装饰器运行啦")func(*args,**kwargs) # 内函数调用外函数变量return inner # 返回内函数@decorate # 相当于 f = decorate(add_num), f(*args,**kwargs)
def add_num(*args,**kwargs):s = 0for i in args:s += ifor i in kwargs.values():s += iprint("和为:", s)add_num(1,2,3,4)结果演示:

5.多重装饰器修饰
- 即一个函数有多个装饰器修饰。
举例:
def make_div(func):print("make_div 装饰器");def inne():result = '<div>' + func() + '</div>'return resultreturn inne;def make_p(func):print("make_p 装饰器");def inne():result = '<p>' + func() + '</p>'return resultreturn inne;@make_div # 当一个函数有多个装饰器时候,谁靠的近先执行谁,
@make_p # 本质上调用的是 f = make_p(content) f1 = make_div(f)
def content():return "人生苦短,我用python"print(content())
运行结果:

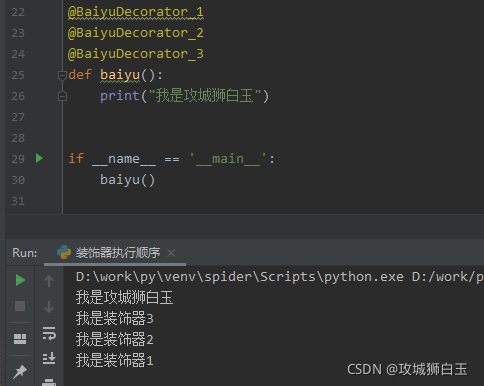
- 主要掌握的是在多重装饰器修饰函数时,装饰器运行的先后顺序:
谁距离被修饰的函数就先用谁修饰
6.返回值是装饰器
按照要求,则返回的是装饰器,则return decorate。
举例:
def return_decorate(flag): # 定义一个函数用来返回装饰器def decorate(func):def inner(a,b):if flag == '+':print("执行的是加法运算")func(a,b)elif flag == '-':print("执行的是减法运算")func(a,b)return inner;return decorate@return_decorate('+') # 实际上执行的是 f = return_decorate('+') f1 = f(add_num) f1(a,b)
def add_num(a,b):print("%d + %d = %d"%(a,b,a+b))@return_decorate('-')
def sub_num(a,b):print("%d - %d = %d"%(a,b,a-b))add_num(2,4)
sub_num(4,2)结果演示:

7.装饰器类
将装饰器函数封装成类,通过
__call__函数将类转化为可调用的对象,用对象调用被修饰的函数
举例:
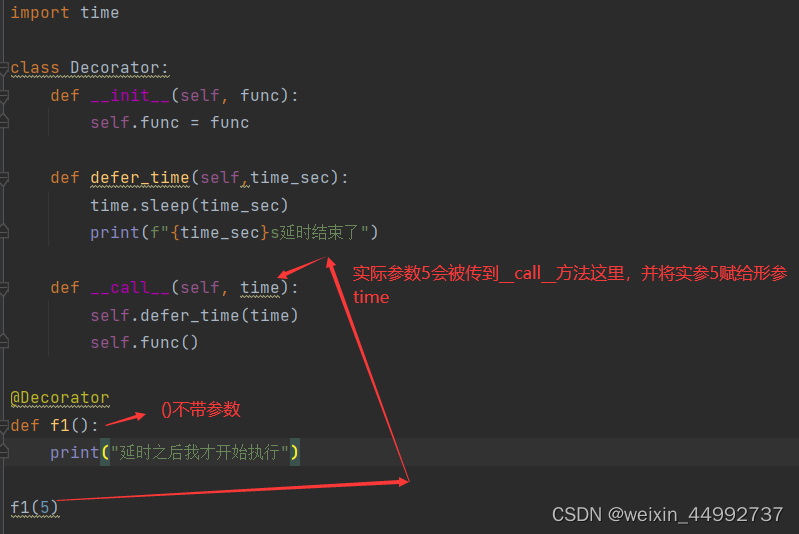
class MyDecorate(object):def __init__(self,func): # 这里相当于将func初始化为类的实例属性,相当于外函数的局部变量self.func = funcdef __call__(self, *args, **kwargs): # 该方法将类变为可调用的对象,可调用的对象能够和函数一样调用使用,这里相当于对inner内函数的相关执行代码进行规范化处理print("装饰器类调用了")self.func(*args,*kwargs)@MyDecorate # f = MyDecorate(show),f(str)
def show(str):print(str)@MyDecorate
def add(a,b):print("%d + %d = %d"%(a,b,a+b))show("加油,奥里给")
add(3,5)
结果展示:

这里的装饰器类,可以大大的增加的代码的通用性,同时需要注意,当类中出现
__call__魔法方法时,该类大概率为装饰器类。