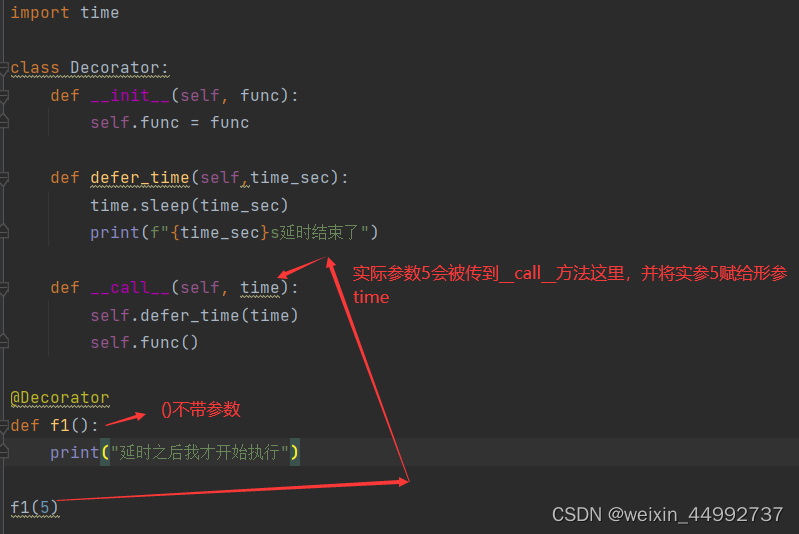
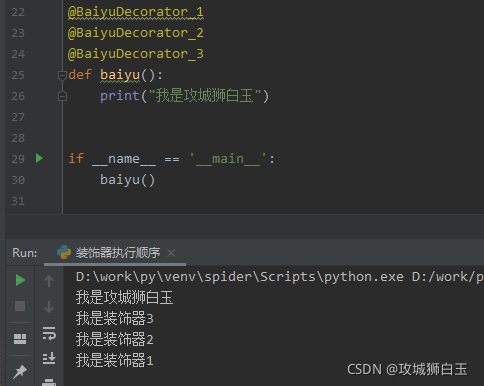
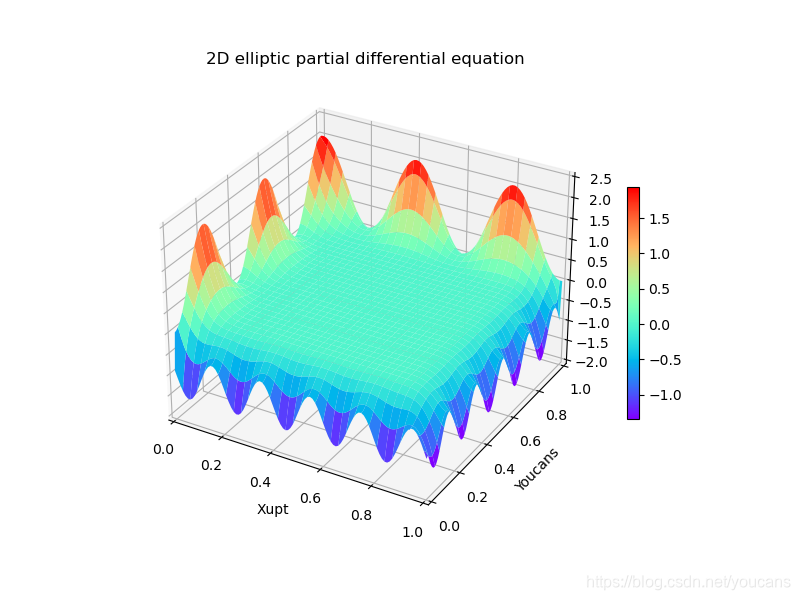
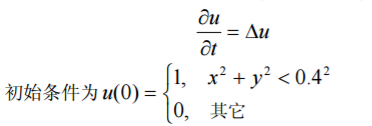一、引出装饰器概念

引入问题：  定义了一个函数，想在运行时动态的增加功能，又不想改动函数本身的代码？

示例：
希望对下列函数调用增加log功能，打印出函数调用：

def f1(x):     return x*2
def f2(x):     return x*x
def f3(x):     return x*x*x

方法一：直接修改原函数的定义

def f1(x):    print 'call f1()' return x*2
def f2(x):    print 'call f2()' return x*x
def f3(x):    print 'call f3()' return x*x*x

思考：高阶函数

(1)、可以接受函数作为参数

(2)、可以返回函数

(3)、那么可否通过接收一个函数，内部对其包装，然后返回一个新函数，这样子动态的增强函数功能

方法二：通过高阶函数返回新函数

def f1(x): return x*2def new_fn(f):'''装饰器函数'''def fn(x):print 'call' + f.__name__ + '()'return f(x)return fng1 = new_fn(f1)
print g1(5)

输出结果：

通过高阶函数达到我们的目的。

但是我们修改程序如下：

def f1(x): return x*2def new_fn(f):'''装饰器函数'''def fn(x):print 'call' + f.__name__ + '()'return f(x)return fnf1 = new_fn(f1)
print f1(5)

输出结果：

是一样的。但是这样子的话，f1的原始定义函数就被彻底隐藏了。

二、装饰器概念

(1)、python内置的 @ 语法就是为了简化装饰器的使用。

进行装饰器的修饰之后：

下面的代码一和代码二在python中是等价的。

代码一：
@new_fn
def f1(x): return x*2print f1(5)

代码二：
def f1(x): return x*2f1 = new_fn(f1)
print f1(5)

输出结果：

是一样的。

装饰器可以这么理解：通过高阶函数传递函数参数，新函数添加旧函数的需求，然后执行旧函数。

三、装饰器作用：可以极大简化代码，避免每个函数编写重复性的代码

(1)、打印日志：@log    (2)、检测性能：@performance

(3)、数据库事务：@transaction   (4)、URL路由：@post('/register')

四、自己总结的装饰器函数三步走

(1)、定义自己先要执行的函数

(2)、

def new_fn(要执行的函数名字):def fn(要执行的参数函数参数/或者没有参数)：添加要添加的函数功能return f(x)  函数的执行结果return fn

(3)、装饰器进行修饰

装饰器的概念差不多就这么多，下面就会详细介绍无参装饰器、有参装饰器。