一，装饰器概念

装饰器本质上还是函数，让其它的函数在不做任何代码修改的情况下，增加额外的功能

所以说一句话：还是函数，记住奥

谈到一个原则：开发封闭原则

概念： 一个以函数作为参数并返回一个替换函数的可执行函数。。装饰器的本质是一个嵌套函数，外层函数的参数是被执行的函数，内层函数是一个闭包并在其中增加新功能（装饰器的功能函数）

这里又提到了闭包，详细了解看这里：

https://mp.csdn.net/mp_blog/creation/editor/123261172

怎么理解？

一个例子：

def f2(func):def f1():x = func()return x + 1return f1
def func():print("输出func()函数")return 1
dec = f2(func)
print(dec())
print(func())

1.函数f2就是一个闭包，传入另一个函数名作为参数。

2.f1()函数为闭包的功能函数，其中调用了func() 函数并将 func( ) 函数的返回值加 1 并返回。

3.每次 f2( ) 函数被调用时，func 的值可能会不同，但无论 func ( ) 代表的何种函数，程序都将调用它.。

4.调用函数dec 和func 函数都将输出 “ func()函数”，dec 返回值为2，func函数的返回值为1。此时称变量dec 是 func 的装饰版。即在 func( ) 函数的基础上增加新的功能。

你这里可以想，你定义的函数返回值为一个函数名，那么在你定义的函数后面再加一个括号是不是就执行的是你函数返回值的函数名的那个函数即：l例如

def f2(func):def f1():return func() + 1return f1
def func():print("输出func()函数")return 1
func = f2(func)
print(func())

二.@符号的使用

上边我们使用变量名将装饰器函数与被装饰函数联系起来。还可以通过@符号和装饰器名实现两者的联系。

示例

：

def f2(func):def f1():return func() + 1return f1
@f2
def func():print("输出func()函数")return 1print(func())

通过@符号和装饰器名实现装饰器函数与被装饰函数联系，当调用func()函数时，程序会自动调用装饰器函数的代码

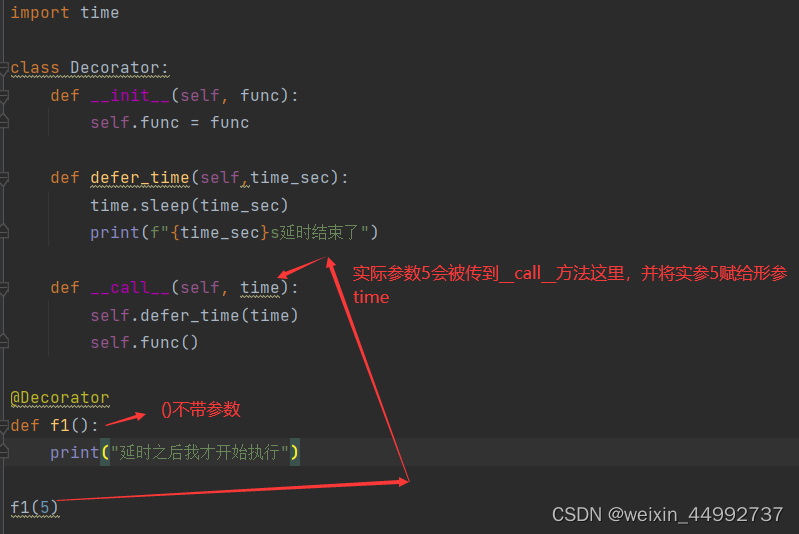
三.有参数函数的装饰

示例：

                 f1()函数中的参数必须包含对应func()函数的参数

def f2(func):def f1(a=0, b=0):print(a,b)return func(a,b) + 1return f1
@f2
def func(a=0, b=0):print("输出func()函数")return a + b
print(func(3,5))

四.带参数的装饰器

因为装饰器也是一个函数，即装饰器本身也可以带参数，此时装饰器需要再多一层的内嵌函数。

第一行先定义装饰器函数，由3个函数嵌套而成，最外层函数有一个装饰器自带的参数，内层函数不变，相当于闭包的嵌套

def f3(arg = '装饰器参数'):def f2(func):def f1():print(arg)return func() + 1return f1return f2
@f3("带参数的装饰器")
def func():print("输出func()函数")return 1
print(func())

这里的装饰器相当于函数名作为形参传入另一个函数中形成的函数调用