看了这篇文章终于搞懂了装饰器，原文有少许错误，但无伤大雅，改正后转载于此，一起学习。

在学习Python的过程中，我相信有很多人和我一样，对Python的装饰器一直觉得很困惑，我也是困惑了好久，并通过思考和查阅才能略有领悟，我希望以下的内容会对你有帮助，我也努力通过通俗的方式使得对Python装饰器的理解更加的透彻。在文中如有遗漏和不足，欢迎交流和指点。
允许转载并注明出处：http://blog.csdn.net/u013471155

很多人对装饰器难以理解，原因是由于以下三点内容没有搞清楚：

关于函数“变量”（或“变量”函数）的理解
关于高阶函数的理解
关于嵌套函数的理解
那么如果能对以上的问题一一攻破，同时遵循装饰器的基本原则，相信会对装饰器有个很好的理解的。那么我们先来看以下装饰器的目的及其原则。

1、装饰器
 

装饰器实际上就是为了给某程序增添功能，但该程序已经上线或已经被使用，那么就不能大批量的修改源代码，这样是不科学的也是不现实的，因为就产生了装饰器，使得其满足：

不能修改被装饰的函数的源代码
不能修改被装饰的函数的调用方式
满足1、2的情况下给程序增添功能
那么根据需求，同时满足了这三点原则，这才是我们的目的。因为，下面我们从解决这三点原则入手来理解装饰器。

等等，我要在需求之前先说装饰器的原则组成：

< 函数+实参高阶函数+返回值高阶函数+嵌套函数+语法糖 = 装饰器 >
这个式子是贯穿装饰器的灵魂所在！

2、需求的实现
 

假设有代码：

import time
def test():time.sleep(2)print("test is running!")
test()

很显然，这段代码运行的结果一定是：等待约2秒后，输出

test is running

• 那么要求在满足三原则的基础上，给程序添加统计运行时间（2 second）功能

在行动之前，我们先来看一下文章开头提到的原因1（关于函数“变量”（或“变量”函数）的理解）

2.1、函数“变量”（或“变量”函数）

假设有代码：

x = 1
y = x
def test1():print("Do something")
test2 = lambda x:x*2

那么在内存中，应该是这样的：

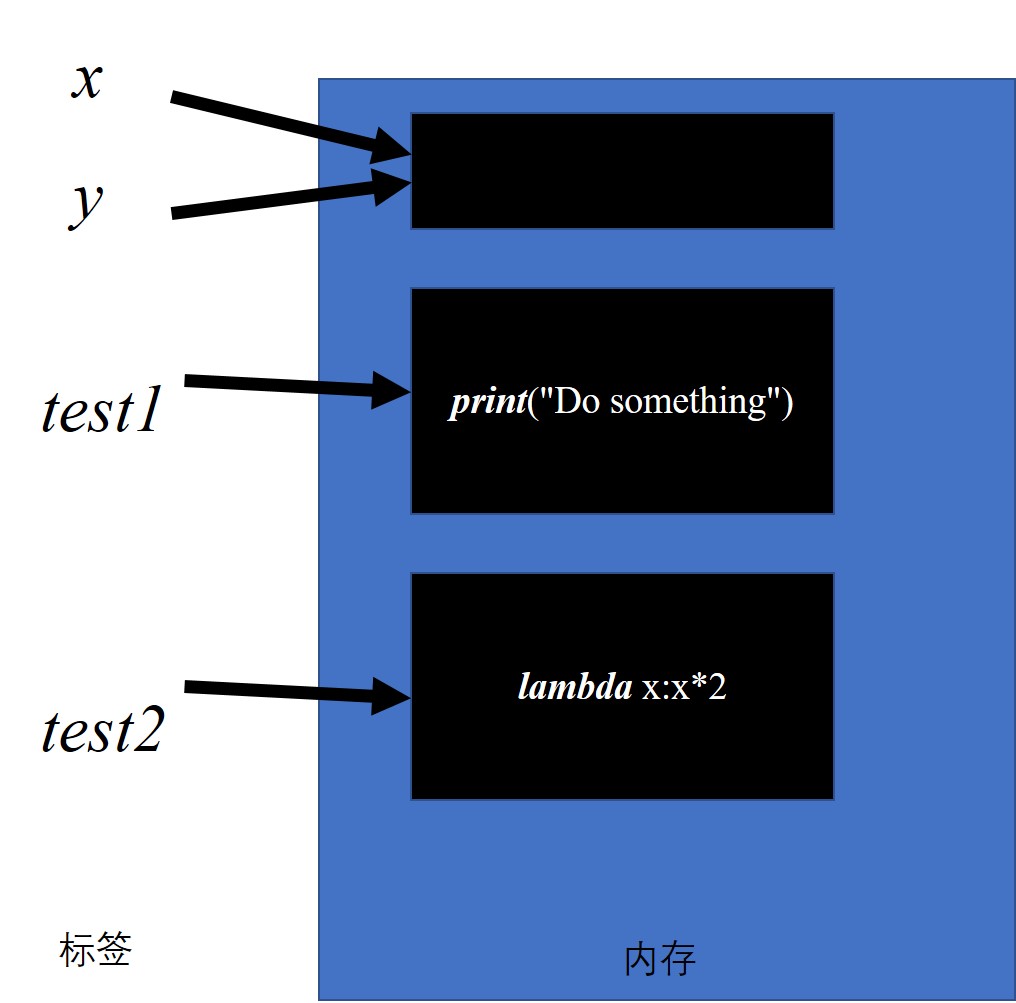
很显然，函数和变量是一样的，都是“一个名字对应内存地址中的一些内容”
那么根据这样的原则，我们就可以理解两个事情：

test1表示的是函数的内存地址
test1()就是调用对在test1这个地址的内容，即函数
如果这两个问题可以理解，那么我们就可以进入到下一个原因(关于高阶函数的理解)

2.2高阶函数

那么对于高阶函数的形式可以有两种：

把一个函数名当作实参传给另外一个函数（“实参高阶函数”）
返回值中包含函数名（“返回值高阶函数”）
那么这里面所说的函数名，实际上就是函数的地址，也可以认为是函数的一个标签而已，并不是调用，是个名词。如果可以把函数名当做实参，那么也就是说可以把函数传递到另一个函数，然后在另一个函数里面做一些操作，根据这些分析来看，这岂不是满足了装饰器三原则中的第一条，即不修改源代码而增加功能。那我们看来一下具体的做法：

还是针对上面那段代码：
 

import timedef test():time.sleep(2)print("test is running!")def deco(func):  start = time.time()func() #2stop = time.time()print(stop-start)deco(test) #1

我们来看一下这段代码，在#1处，我们把test当作实参传递给形参func，即func=test。注意，这里传递的是地址，也就是此时func也指向了之前test所定义的那个函数体，可以说在deco()内部，func就是test。在#2处，把函数名后面加上括号，就是对函数的调用（执行它）。因此，这段代码运行结果是：

test is running!
the run time is 3.0009405612945557

我们看到似乎是达到了需求，即执行了源程序，同时也附加了计时功能，但是这只满足了原则1（不能修改被装饰的函数的源代码），但这修改了调用方式。假设不修改调用方式，那么在这样的程序中，被装饰函数就无法传递到另一个装饰函数中去。

那么再思考，如果不修改调用方式，就是一定要有test()这条语句，那么就用到了第二种高阶函数，即返回值中包含函数名

如下代码：
 

import timedef test():time.sleep(2)print("test is running!")def deco(func):  print(func)return func 
t = deco(test) #3
#t()#4test()

我们看这段代码，在#3处，将test传入deco()，在deco()里面操作之后，最后返回了func，并赋值给t。因此这里test => func => t，都是一样的函数体。最后在#4处保留了原来的函数调用方式。
看到这里显然会有些困惑，我们的需求不是要计算函数的运行时间么，怎么改成输出函数地址了。是因为，单独采用第二张高阶函数（返回值中包含函数名）的方式，并且保留原函数调用方式，是无法计时的。如果在deco()里计时，显然会执行一次，而外面已经调用了test()，会重复执行。这里只是为了说明第二种高阶函数的思想，下面才真的进入重头戏。

2.3 嵌套函数

嵌套函数指的是在函数内部定义一个函数，而不是调用，如：
 

def func1():def func2():pass
而不是
def func1():func2()

另外还有一个题外话，函数只能调用和它同级别以及上级的变量或函数。也就是说：里面的能调用和它缩进一样的和他外部的，而内部的是无法调用的。

那么我们再回到我们之前的那个需求，想要统计程序运行时间，并且满足三原则。

代码：

import timedef timer(func): #5def deco():  start = time.time()func()stop = time.time()print(stop-start)return deco#test = timer(test) #6 // 原文此处有误，应该放到函数定义后面def test():time.sleep(2)print("test is running!")   test = timer(test) #6
test() #7

 

这段代码可能会有些困惑，怎么忽然多了这么多，暂且先接受它，分析一下再来说为什么是这样。

首先，在#6处，把test作为参数传递给了timer()，此时，在timer()内部，func = test，接下来，定义了一个deco()函数，当并未调用，只是在内存中保存了，并且标签为deco。在timer()函数的最后返回deco()的地址deco。

然后再把deco赋值给了test，那么此时test已经不是原来的test了，也就是test原来的那些函数体的标签换掉了，换成了deco。那么在#7处调用的实际上是deco()。

那么这段代码在本质上是修改了调用函数，但在表面上并未修改调用方式，而且实现了附加功能。

那么通俗一点的理解就是：
把函数看成是盒子，test是小盒子，deco是中盒子，timer是大盒子。程序中，把小盒子test传递到大盒子temer中的中盒子deco，然后再把中盒子deco拿出来，打开看看（调用）

这样做的原因是：

我们要保留test()，还要统计时间，而test()只能调用一次（调用两次运行结果会改变，不满足），再根据函数即“变量”，那么就可以通过函数的方式来回闭包。于是乎，就想到了，把test传递到某个函数，而这个函数内恰巧内嵌了一个内函数，再根据内嵌函数的作用域（可以访问同级及以上，内嵌函数可以访问外部参数），把test包在这个内函数当中，一起返回，最后调用这个返回的函数。而test传递进入之后，再被包裹出来，显然test函数没有弄丢（在包裹里），那么外面剩下的这个test标签正好可以替代这个包裹（内含test()）。
 

 

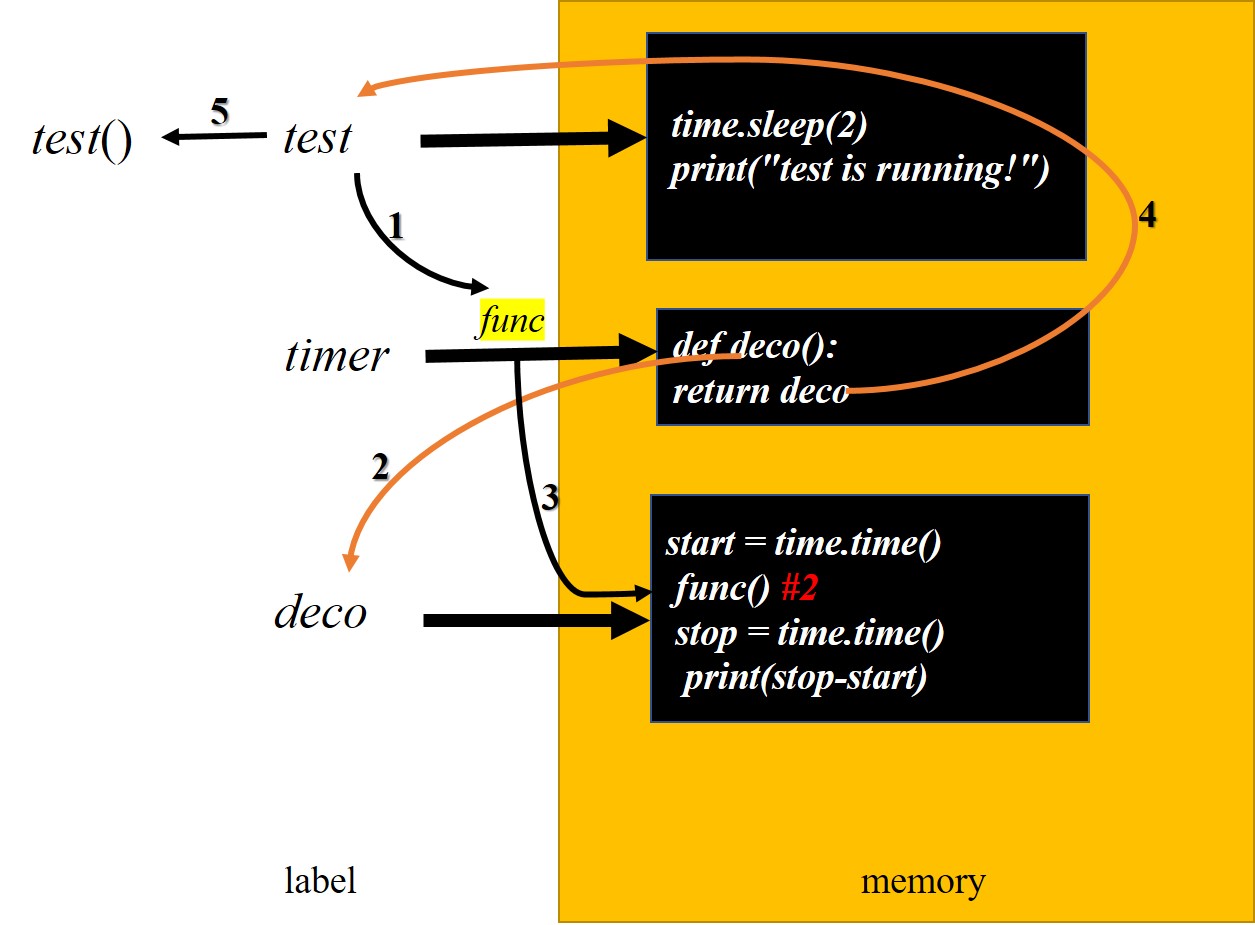
至此，一切皆合，大功告成，单只差一步。

3、 真正的装饰器

根据以上分析，装饰器在装饰时，需要在每个函数前面加上：

test = timer(test)

显然有些麻烦，Python提供了一种语法糖，即：

@timer

这两句是等价的，只要在函数前加上这句，就可以实现装饰作用。

以上为无参形式

4、装饰有参函数

import timedef timer(func)def deco():  start = time.time()func()stop = time.time()print(stop-start)return deco@timer
def test(parameter): #8time.sleep(2)print("test is running!")   
test() 

对于一个实际问题，往往是有参数的，如果要在#8处，给被修饰函数加上参数，显然这段程序会报错的。错误原因是test()在调用的时候缺少了一个位置参数的。而我们知道test = func = deco，因此test()=func()=deco()
,那么当test(parameter)有参数时，就必须给func()和deco()也加上参数，为了使程序更加有扩展性，因此在装饰器中的deco()和func()，加如了可变参数*agrs和 **kwargs。

完整代码如下：
 

import timedef timer(func):def deco(*args, **kwargs):  start = time.time()func(*args, **kwargs)stop = time.time()print(stop-start)return deco@timer
def test(parameter): #8time.sleep(2)print("test is running!")   
test() 

那么我们再考虑个问题，如果原函数test()的结果有返回值呢？比如：

def test(parameter): time.sleep(2)print("test is running!")   return "Returned value"

那么面对这样的函数，如果用上面的代码来装饰，最后一行的test()实际上调用的是deco()。有人可能会问，func()不就是test()么，怎么没返回值呢？

其实是有返回值的，但是返回值返回到deco()的内部，而不是test()即deco()的返回值，那么就需要再返回func()的值，因此就是：
 

def timer(func): # 原文这里少了冒号def deco(*args, **kwargs):  start = time.time()res = func(*args, **kwargs)#9stop = time.time()print(stop-start)return res#10return deco

其中，#9的值在#10处返回。
 

完整程序为：

import timedef timer(func):def deco(*args, **kwargs):  start = time.time()res = func(*args, **kwargs)stop = time.time()print(stop-start)return res return deco@timer
def test(parameter): #8time.sleep(2)print("test is running!")   return "Returned value"
test() 

 

5、带参数的装饰器

又增加了一个需求，一个装饰器，对不同的函数有不同的装饰。那么就需要知道对哪个函数采取哪种装饰。因此，就需要装饰器带一个参数来标记一下。例如：

@decorator(parameter = value)

比如有两个函数：

def task1():time.sleep(2)print("in the task1")def task2():time.sleep(2)print("in the task2")task1()
task2()

要对这两个函数分别统计运行时间，但是要求统计之后输出：

the task1/task2 run time is : 2.00……

于是就要构造一个装饰器timer，并且需要告诉装饰器哪个是task1，哪个是task2，也就是要这样：

@timer(parameter='task1') #
def task1():time.sleep(2)print("in the task1")@timer(parameter='task2') #
def task2():time.sleep(2)print("in the task2")task1()
task2()

那么方法有了，但是我们需要考虑如何把这个parameter参数传递到装饰器中，我们以往的装饰器，都是传递函数名字进去，而这次，多了一个参数，要怎么做呢？
于是，就想到再加一层函数来接受参数，根据嵌套函数的概念，要想执行内函数，就要先执行外函数，才能调用到内函数，那么就有：

def timer(parameter): #print("in the auth :", parameter)def outer_deco(func): #print("in the outer_wrapper:", parameter)def deco(*args, **kwargs):return decoreturn outer_deco

 首先timer(parameter)，接收参数parameter=’task1/2’，而@timer(parameter)也恰巧带了括号，那么就会执行这个函数， 那么就是相当于：

timer = timer(parameter)
task1 = timer(task1)

后面的运行就和一般的装饰器一样了：

import timedef timer(parameter):def outer_wrapper(func):def wrapper(*args, **kwargs):if parameter == 'task1':start = time.time()func(*args, **kwargs)stop = time.time()print("the task1 run time is :", stop - start)elif parameter == 'task2':start = time.time()func(*args, **kwargs)stop = time.time()print("the task2 run time is :", stop - start)return wrapperreturn outer_wrapper@timer(parameter='task1')
def task1():time.sleep(2)print("in the task1")@timer(parameter='task2')
def task2():time.sleep(2)print("in the task2")task1()
task2()

至此，装饰器的全部内容结束。