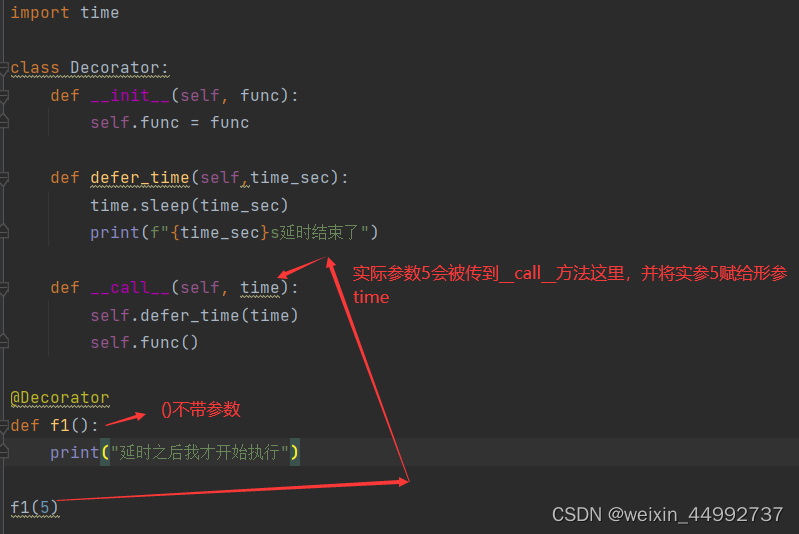
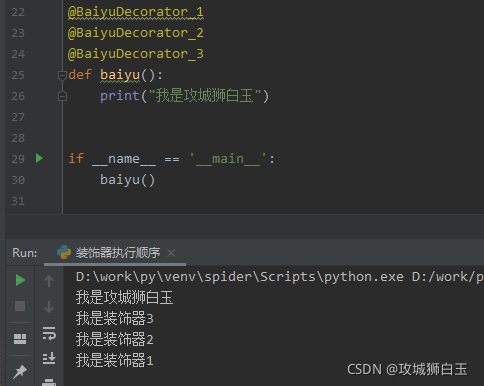
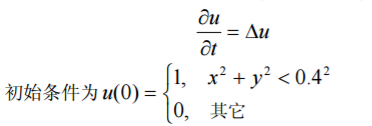Decorator 装饰器是一项实验性特性,在未来的版本中可能会发生改变
它们不仅增加了代码的可读性,清晰地表达了意图,而且提供一种方便的手段,增加或修改类的功能
若要启用实验性的装饰器特性,你必须在命令行或tsconfig.json里启用编译器选项
装饰器
装饰器是一种特殊类型的声明,它能够被附加到类声明,方法, 访问符,属性或参数上。
首先定义一个类
class A {constructor() {}
}定义一个类装饰器函数 他会把ClassA的构造函数传入你的watcher函数当做第一个参数
const watcher: ClassDecorator = (target: Function) => {target.prototype.getParams = <T>(params: T):T => {return params}
}使用的时候 直接通过@函数名使用
@watcher
class A {constructor() {}
}验证
const a = new A();
console.log((a as any).getParams('123'));装饰器工厂
其实也就是一个高阶函数 外层的函数接受值 里层的函数最终接受类的构造函数
const watcher = (name: string): ClassDecorator => {return (target: Function) => {target.prototype.getParams = <T>(params: T): T => {return params}target.prototype.getOptions = (): string => {return name}}
}@watcher('name')
class A {constructor() {}
}const a = new A();
console.log((a as any).getParams('123'));装饰器组合
就是可以使用多个装饰器
const watcher = (name: string): ClassDecorator => {return (target: Function) => {target.prototype.getParams = <T>(params: T): T => {return params}target.prototype.getOptions = (): string => {return name}}
}
const watcher2 = (name: string): ClassDecorator => {return (target: Function) => {target.prototype.getNames = ():string => {return name}}
}@watcher2('name2')
@watcher('name')
class A {constructor() {}
}const a = new A();
console.log((a as any).getOptions());
console.log((a as any).getNames());方法装饰器
返回三个参数
- 对于静态成员来说是类的构造函数,对于实例成员是类的原型对象。
- 成员的名字。
- 成员的属性描述符。
[{},'setParasm',{value: [Function: setParasm],writable: true,enumerable: false,configurable: true}
]const met:MethodDecorator = (...args) => {console.log(args);
}class A {constructor() {}@metgetName ():string {return '小满'}
}const a = new A();属性装饰器
返回两个参数
- 对于静态成员来说是类的构造函数,对于实例成员是类的原型对象。
- 属性的名字。
[ {}, 'name', undefined ]
const met:PropertyDecorator = (...args) => {console.log(args);
}class A {@metname:stringconstructor() {}}const a = new A();参数装饰器
返回三个参数
- 对于静态成员来说是类的构造函数,对于实例成员是类的原型对象。
- 成员的名字。
- 参数在函数参数列表中的索引。
[ {}, 'setParasm', 0 ]
const met:ParameterDecorator = (...args) => {console.log(args);
}class A {constructor() {}setParasm (@met name:string = '213') {}
}const a = new A();元数据存储
import 'reflect-metadata'可以快速存储元数据然后在用到的地方取出来 defineMetadata getMetadata
//1.类装饰器 ClassDecorator
//2.属性装饰器 PropertyDecorator
//3.参数装饰器 ParameterDecorator
//4.方法装饰器 MethodDecorator PropertyDescriptor 'https://api.apiopen.top/api/getHaoKanVideo?page=0&size=10'
//5.装饰器工厂
import axios from 'axios'
import 'reflect-metadata'
const Base = (base:string) => {const fn:ClassDecorator = (target) => {target.prototype.base = base;}return fn
} const Get = (url:string) => {const fn:MethodDecorator = (target:any,key,descriptor:PropertyDescriptor) => {axios.get(url).then(res=>{const key = Reflect.getMetadata('key',target)descriptor.value(key ? res.data[key] : res.data)})}return fn
}const result = () => {const fn:ParameterDecorator = (target:any,key,index) => {Reflect.defineMetadata('key','result',target)}return fn
}const Bt:PropertyDecorator = (target,key) => {console.log(target,key)
}@Base('/api')
class Http {@Btxiaoman:stringconstructor () {this.xiaoman = 'xiaoman'}@Get('https://api.apiopen.top/api/getHaoKanVideo?page=0&size=10')getList (@result() data:any) {// console.log(data)}// @Post('/aaaa')create () {}
}const http = new Http() as any// console.log(http.base)学习TypeScript21(Rollup构建TS项目)_qq1195566313的博客-CSDN博客