Linux Mysql自动备份

article/2025/9/18 5:38:24

1.配置自动备份环境

1.1 创建文件见放脚本文件和备份数据

# 创建/data/backup/mysqlmkdir -p /data/backup/mysqlcd /data/backup# 创建mysql_backup.sh的脚本并且填充数据vi mysql_backup.sh# vi mysql_backup.sh进行编辑和修改

1.2 创建备份数据的语句 mysql_backup.sh 用于备份数据

#!/bin/bash# 需要的话，自己改这里哦#db_user='root'#db_password=`cat /data/www/mysql_password`db_name='baizhan'backup_dir='/data/backup/mysql/'current_time=$(date +'%Y-%m-%d_%H%M%S')filepath=$backup_dir$current_time'.sql.gz'#此处没有使用 $db_password $db_user, 已经写入到配置文件中echo '开始导出数据库...'mysqldump --defaults-extra-file=/data/backup/my_mysql.cnf  $db_name | gzip > $filepathecho '导出成功，文件名为: '$filepath

1.3 配置my_mysql.cnf的数据

vi my_mysql.cnf

[mysqldump]max_allowed_packet= 400Mhost=127.0.0.1user=rootpassword='12346' # 设置为自己的密码例如我的为123456[mysql]host=127.0.0.1user=rootpassword='123465'

1.4 脚本增加权限

chmod +x ./mysql_backup.sh

1.5 TEST 测试是否可以导出成功

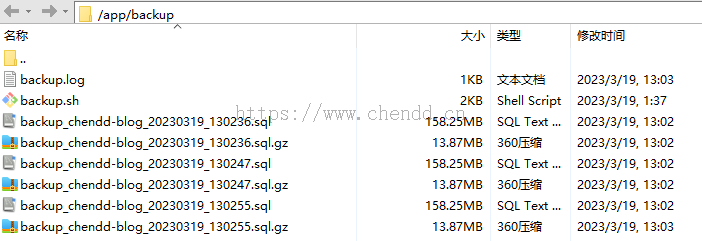
sh ./mysql_backup.sh# 查看一下结果ll ./mysql

配置关于自动恢复数据的脚本

2.1 创建脚本命令

vi mysql_restore.sh

2.2 放入脚本命令

#!/bin/bash
if [ -z $1 ] || [ ! -f $1 ]
thenecho "请输入sql压缩文件(*.sql.gz)"exit 1
fi
db_name='fs'#需要导入的的数据名
base_dir='/data/backup/mysql/'
gz_sql_file=`basename $1`file_ext=${gz_sql_file##*.}
if [ $file_ext != 'gz' ]
thenecho '文件格式不正确，请输入 .sql.gz 文件'exit 1
fi
sql_file=${gz_sql_file%.*}
echo '解压文件中...'
gzip -dc $base_dir$gz_sql_file > $base_dir$sql_file
echo '解压完成.'
echo '开始导入数据库...'
mysql --defaults-extra-file=/data/backup/my_mysql.cnf $db_name < $base_dir$sql_file
if [ -f $base_dir$sql_file ]
thenecho '删除临时文件.'rm -f $base_dir$sql_file
fi
echo '导入完成.'

2.3 赋予权限并且执行

# 权限赋予chmod +x ./mysql_restore.sh# 导入测试sh ./mysql_restore.sh  ./mysql/2021-12-28_111334.sql.gz

创建计划任务

3.1 关于crontab

crontab命令常见于Unix和Linux的操作系统之中，用于设置周期性被执行的指令。该命令从标准输入设备读取指令，并将其存放于“crontab”文件中，以供之后读取和执行。通常，crontab储存的指令被守护进程激活。crond常常在后台运行，每一分钟检查是否有预定的作业需要执行。这类作业一般称为cron jobs。

3.2 关于备份的时间

例子

30 21 * * * /usr/local/etc/rc.d/lighttpd restart #每晚的21:30重启apache。

45 4 1,10,22 * * /usr/local/etc/rc.d/lighttpd restart #每月1、10、22日的4 : 45重启apache。

10 1 * * 6,0 /usr/local/etc/rc.d/lighttpd restart #每周六、周日的1 : 10重启apache

0,30 18-23 * * * /usr/local/etc/rc.d/lighttpd restart #每天18 : 00至23 : 00之间每隔30分钟重启apache。0 23 * * 6 /usr/local/etc/rc.d/lighttpd restart #每星期六的11 : 00 pm重启apache。

* */1 * * * /usr/local/etc/rc.d/lighttpd restart #每一小时重启apache

* 23-7/1 * * * /usr/local/etc/rc.d/lighttpd restart #晚上11点到早上7点之间，每隔一小时重启apache

0 11 4 * mon-wed /usr/local/etc/rc.d/lighttpd restart #每月的4号与每周一到周三的11点重启apache

0 4 1 jan * /usr/local/etc/rc.d/lighttpd restart #一月一号的4点重启apache

*/30 * * * * /usr/sbin/ntpdate 210.72.145.44 #每半小时同步一下时间

详解看此处 crontab详解 - 老董 - 博客园

3.3 具体使用

crontab -e#粘贴下面的内容， 大家根据自己的需要更改就可以了0 1,12 * * * /data/backup/mysql_backup.sh # 每天凌晨1点，中午12点备份一次数据#大家可以先使用下面这条做为测试哦，1分钟跑一次，我们只需要查看 ll /data/backup/mysql 这个文件夹就好了*/1 * * * * /data/backup/mysql_backup.sh

自动备份文件自动删除

4.1 创建删除脚本文件 remove_backup.sh

vi remove_backup.sh# 复制下面的脚本内容#/bin/bash# 删除30天前的备份find /data/backup/mysql -type f -mtime +30 | xargs rm -f#可执行权限chmod +x ./remove_backup.sh

4.2 配置自动删除

crontab -e #下面这个就是脚本内容哦，添加这一句0 1 * * * /data/backup/remove_backup.sh # 每天凌晨1点，自动删除30天前的备份

windos自动下载linux的数据

5.1 安装WinSCP

WinSCP :: Official Site :: Download windscp下载

5.2 安装WinSCP 步骤

https://jingyan.baidu.com/article/9f7e7ec0ccdb476f2815542c.html

5.3 配置bat文件

1.先在winscp 登录自己的linux的账号密码

2.复制winscp生成好的批处理文件信息

3.新建一个bat文件将第二步的文件内容复制进去

@echo off
"C:\Users\Administrator\AppData\Local\Programs\WinSCP\WinSCP.com" ^ # 安装的winscp/log="G:\log\WinSCP.log" /ini=nul ^ # 日志记录地方/command ^"open sftp://root:feisu@192.168.216.130/ -hostkey=""ssh-ed25519 255 p5R5ttEPqk/fNyNrEVfK3/CwNbX57WuYI6hzfz/C7jk=""" ^"option transfer binary" ^ #二进制传输"get /data/backup/mysql/*2021*.sql.gz G:\data_bak\V3\" ^ # 将linux指定位置传输到本地指定位置"exit"
set WINSCP_RESULT=%ERRORLEVEL%
if %WINSCP_RESULT% equ 0 (echo Success
) else (echo Error
)
exit /b %WINSCP_RESULT%

5.4 配置任务计划自动进行运行bat进行下载

任务计划程序(让计算机自动执行程序) - 平凡的神灯 - 博客园