最近在使用tensorflow完成句子相似度建模等任务时常常会用到各种距离的计算,而且有很多论文提出了Attention机制,所以这里就介绍一下如何使用tensorflow实现上述各种功能。
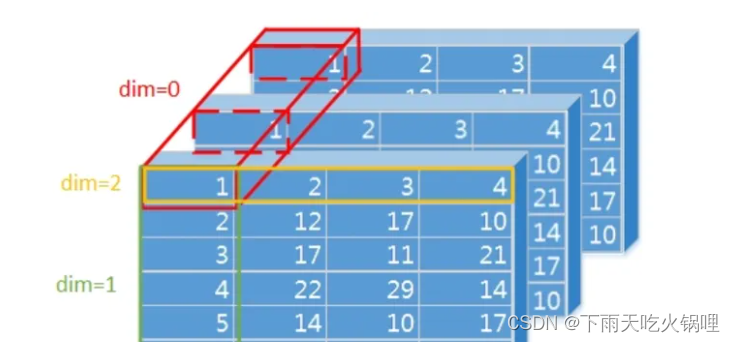
这里首先假定我们的输入是两个四维的Tensor,然后我们需要计算的是其中某个维度的距离。比如说我们的输入是batch个句子,句长是sent_len, 每个词被表示成embed_size的词向量。所以我们的输入就是一个[batch_size, sent_len, embed_size, 1]的Tensor,需要计算的就是两个句子的Attention矩阵。Aij表示句子1中第i个单词和句子2中第j个单词的距离(余弦距离,欧氏距离,L1距离等),也就是计算两个长度为embed_size的向量之间的距离。
为了方便表示和调试,我们这里使用shape为[2,3,4,1]的Tensor来表示上述句子。
1,Euclidean distance
欧氏距离很简单,以向量为例(x1, x2, x3,….,xn),(y1, y2, y3,….,yn),那么其欧氏距离的计算公式如下图所示:

在tensorflow中如何实现呢,代码如下:
import tensorflow as tf
x3 = tf.constant([[[[1], [2], [3], [4]],
[[5], [6], [7], [8]],
[[9], [10], [11], [12]]],
[[[1], [2], [3], [4]],
[[5], [6], [7], [8]],
[[9], [10], [11], [12]]]], tf.float32)
x4 = tf.constant([[[[3], [4], [1], [2]],
[[5], [7], [8], [6]],
[[9], [12], [11], [10]]],
[[[1], [2], [3], [4]],
[[5], [6], [7], [8]],
[[9], [10], [11], [12]]]], tf.float32)
with tf.Session() as sess:
dis = sess.run(tf.square(x3-x4))
dis1 = sess.run(tf.reduce_sum(tf.square(x3-x4), 2))
euclidean = sess.run(tf.sqrt(tf.reduce_sum(tf.square(x3-x4), 2)))
print dis, dis1, euclidean
这部分代码实现的功能是:我们有x3,x4两个输入,每个有两句话,每句话有三个单词。计算的是对应单词之间的距离。下面是输出:
dis:
[[[[ 4.]
[ 4.]
[ 4.]
[ 4.]]
[[ 0.]
[ 1.]
[ 1.]
[ 4.]]
[[ 0.]
[ 4.]
[ 0.]
[ 4.]]]
[[[ 0.]
[ 0.]
[ 0.]
[ 0.]]
[[ 0.]
[ 0.]
[ 0.]
[ 0.]]
[[ 0.]
[ 0.]
[ 0.]
[ 0.]]]]
dis1:
[[[ 16.]
[ 6.]
[ 8.]]
[[ 0.]
[ 0.]
[ 0.]]]
Euclidean:
[[[ 3.99999976]
[ 2.44948959]
[ 2.82842684]]
[[ 0. ]
[ 0. ]
[ 0. ]]]
所以Euclidean距离的计算方法就是:
euclidean = tf.sqrt(tf.reduce_sum(tf.square(x3-x4), 2))
余弦距离
跟Euclidean距离相似,余弦距离也可以用来表征两个向量之间的相似度。其计算公式如下图所示:

在tensorflow中实现方法如下,这里我们仍然沿用x3,x4的定义,之写出sess.run()部分的代码:
with tf.Session() as sess:
#求模
x3_norm = tf.sqrt(tf.reduce_sum(tf.square(x3), axis=2))
x4_norm = tf.sqrt(tf.reduce_sum(tf.square(x4), axis=2))
#内积
x3_x4 = tf.reduce_sum(tf.multiply(x3, x4), axis=2)
cosin = x3_x4 / (x3_norm * x4_norm)
cosin1 = tf.divide(x3_x4, tf.multiply(x3_norm, x4_norm))
a, b, c, d, e = sess.run([x3_norm, x4_norm, x3_x4, cosin, cosin1])
print a, b, c, d, e
上述代码按照cosine的计算公式进行分步求解。最终的到了两个句子对应词之间的余弦距离。从结果会看出cosin和cosin1是一样的。结果如下所示:
x3_norm:
[[[ 5.47722483]
[ 13.19090366]
[ 21.11871338]]
[[ 5.47722483]
[ 13.19090557]
[ 21.11871147]]]
x4_norm:
[[[ 5.47722483]
[ 13.19090366]
[ 21.11871338]]
[[ 5.47722483]
[ 13.19090557]
[ 21.11871147]]]
x3_x4:
[[[ 22.]
[ 171.]
[ 442.]]
[[ 30.]
[ 174.]
[ 446.]]]
cosin:
[[[ 0.73333353]
[ 0.98275894]
[ 0.99103123]]
[[ 1.00000024]
[ 1.00000012]
[ 1.00000012]]]
cosin1:
[[[ 0.73333353]
[ 0.98275894]
[ 0.99103123]]
[[ 1.00000024]
[ 1.00000012]
[ 1.00000012]]]
Attention矩阵计算
如上面提到的那样,Attention矩阵A中的每个元素Aij表示句子1中第i个单词和句子2中第j个单词的距离。那么如何实现呢。我们先介绍一种比较简单的思路:
def input_attention(x1, x2):
#将每个句子按单词进行切分
x1_unstack = tf.unstack(x1, axis=1)
x2_unstack = tf.unstack(x2, axis=1)
D = []
for i in range(len(x1_unstack)):
d = []
for j in range(len(x2_unstack)):
#计算两个单词之间的相似度距离
dis = tf.sqrt(tf.reduce_sum(tf.square(x1_unstack[i]- x2_unstack[j]), axis=1))
d.append(dis)
D.append(d)
D1 = tf.reshape(D, [2, 3, 3])
D2 = tf.reshape(tf.transpose(D, perm=[2, 0, 1, 3]), [2,3,3])
return D1, D2
with tf.Session() as sess:
A, A1 = input_attention(x3, x4)
a, a1 = sess.run([A, A1])
print a, a1
这种方法是先将句子进行unstack,也就是“分词”。经过下面这行命令我们就得到了3个[2, 4, 1]的tensor。即3个单词
x1_unstack = tf.unstack(x1, axis=1)
所以下面这条命令之后我们就得到一个[2, 1]的tensor。在经过两个循环(3×3),我们就获得了[3, 3, 2, 1]的tensor。D是一开始我用的,当时觉得是没问题的,但是经过调试发现,他返回的结果是错误的,因为D是[3,3,2,1],2在最里面,reshape时不会被直接调到外面。结果如下所示:
dis = tf.sqrt(tf.reduce_sum(tf.square(x1_unstack[i]- x2_unstack[j]), axis=1))
A:
[[[ 4. 0. 8.36660004]
[ 8. 16.24807739 16. ]
[ 8.94427204 8. 2.44948983]]
[[ 0. 8.48528099 8. ]
[ 16.4924221 16. 8.36660004]
[ 8. 2.82842708 0. ]]]
A1:
[[[ 4. 8.36660004 16.24807739]
[ 8.94427204 2.44948983 8.48528099]
[ 16.4924221 8.36660004 2.82842708]]
[[ 0. 8. 16. ]
[ 8. 0. 8. ]
[ 16. 8. 0. ]]]
根据上面的结果,我们很明显可以看出A1才是我们想要的数据。