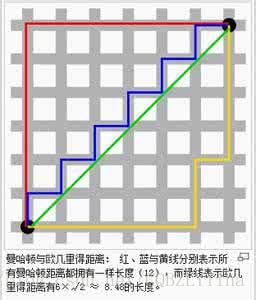
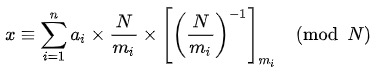[*] Lau B , Sprunk C , Burgard W . Improved updating of Euclidean distance maps and Voronoi diagrams[C]// IEEE/RSJ International Conference on Intelligent Robots & Systems. IEEE, 2010.

本文对[*]中的Occupancy Map to Euclidean Distance Maps算法进行python实现。

论文中相关算法如下所示：

该算法能够根据加入或移除占据栅格地图的障碍物进行更新一幅欧式距离地图。

其中，论文中解释了pop(open)与insert(open, s, d)两个未给出伪代码的函数。文中说，pop（open）是从open中找到距离最小的一个元素返回，并从open中删除。在实现过程中，按照最小距离返回时，当从有多个障碍物的地图中移除掉一个障碍物时，程序会陷入无止尽的循环。经验证，如果按照最大距离返回时，可正常运行。

论文中也补充到，给每个栅格增加一个属性：process，来达到类似于加入open与移除open队列的目的。

算法python实现

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
open_list = []dist = 99999.0*np.ones((30, 30))
obst = -1*np.ones((30, 30))
toRaise = np.zeros((30, 30))
process = np.zeros((30, 30))def S2IJ(s):i = int(s//30)j = int(s%30)return i,jdef SetObstacle(i,j):obst[i,j] = i*30+jdist[i,j] = 0process[i,j] = 1
#     open_list.append([i,j])def RemoveObstacle(i,j):obst[i,j] = -1toRaise[i,j] = 1dist[i, j] = 99999.0process[i, j] = 1
#     open_list.append([i,j])def Raise(i,j):for ni in [-1, 0, 1]:for nj in [-1, 0, 1]:if ni == 0 and nj == 0:continuexi = i + nixj = j + njif xi < 0 or xi >= 30 or xj < 0 or xj >= 30:continueif (obst[xi, xj] >= 0) and (toRaise[xi, xj] == 0):oi, oj = S2IJ(obst[xi,xj])  if (oi != xi) or (oj != xj):dist[xi,xj] = 99999.0
#                     print(xi,xj,oi,oj,obst[xi, xj])obst[xi, xj] = -1toRaise[xi, xj] = 1
#                 else:
#                     for i in range(30):
#                         for j in range(30):
#                             toRaise[i,j] = 0process[xi, xj] = 1
#                 open_list.append([xi, xj])toRaise[i,j] = 0def Lower(i, j):si, sj = S2IJ(obst[i, j])for ni in [-1, 0, 1]:for nj in [-1, 0, 1]:if ni == 0 and nj == 0:continuexi = i + nixj = j + njif xi < 0 or xi >= 30 or xj < 0 or xj >= 30:continue            if toRaise[xi, xj] == 0:d = np.sqrt((si-xi)*(si-xi)+(sj-xj)*(sj-xj))if (d < dist[xi, xj]) or (obst[xi, xj] < 0):dist[xi, xj] = dobst[xi, xj] = si*30+sjprocess[xi, xj] = 1
#                     open_list.append([xi, xj])def Pops(): # get the element with max distancemax_index = -1max_dist = -1.0for i in range(30):for j in range(30):if process[i,j] == 1:if dist[i,j] > max_dist:max_dist = dist[i,j]max_index = i*30+jif max_index < 0:return False, max_indexelse:oi, oj = S2IJ(max_index)process[oi, oj] = 0return True, max_indexdef UpdateDistanceMap():not_empty, s = Pops()while not_empty:i,j = S2IJ(s)if toRaise[i,j] == 1:Raise(i,j)   
#             print("raise")
#             print(i,j)else:if obst[i,j] >= 0:Lower(i,j)
#                 print("lower")
#                 print(i,j)not_empty, s = Pops()

从空白地图上加入一个障碍物

SetObstacle(15, 15)
%time UpdateDistanceMap()
plt.imshow(dist)
plt.show()

时间成本：
Wall time: 325 ms

欧式距离地图：

增加一个障碍物

SetObstacle(5,5)
%time UpdateDistanceMap()
plt.imshow(dist)
plt.show()

时间成本：
Wall time: 93.8 ms

欧式距离地图：

再增加一个障碍物

SetObstacle(10, 25)
%time UpdateDistanceMap()
plt.imshow(dist)
plt.show()

时间成本：
Wall time: 71.9 ms

欧式距离地图：

从地图上移除一个障碍物

RemoveObstacle(5,5)
%time UpdateDistanceMap()
plt.imshow(dist)
plt.show()

时间成本：
Wall time: 854 ms

欧式距离地图：

重新加入一个新的障碍物

SetObstacle(25,25)
%time UpdateDistanceMap()
plt.imshow(dist)
plt.show()

时间成本
Wall time: 58.6 ms

欧式距离地图

补充

欧式距离地图可进一步得到Voronoi地图（如论文中给出的例子）：

我们仔细观察以上程序中生成的欧式距离地图，也发现障碍物之间有类似边界的栅格：

因此，得到欧式距离地图后，可以很方便的得到Voronoi地图。

结论

欧式距离地图生成的时间成本很高，几乎不能用于无人驾驶局部代价地图生成。但是可以应用于相对静态的场景中。

---

补充20220622

原问题地址如下：
Improved updating of Euclidean distance maps and Voronoi diagrams问题
将问题引在此处：
通过读您对于这篇论文的解读，想要问您一个问题，即在整个地图中，是否Raise状态是只有碰到了边界或被占用的格子，才会停止传播raise并反向传播lower，并且传播lower的过程，是否为，所有的被占据的格子都要反向传播lower，有更省算力的方案吗

本人给出的解答如下：

有更省力的方案，先贴出更新后的代码：

def Raise(i,j):for ni in [-1, 0, 1]:for nj in [-1, 0, 1]:if ni == 0 and nj == 0:continuexi = i + nixj = j + njif xi < 0 or xi >= 30 or xj < 0 or xj >= 30:continueif (obst[xi, xj] >= 0) and (toRaise[xi, xj] == 0):oi, oj = S2IJ(obst[xi,xj])  if (obst[oi, oj] == -1): # 将原条件  ((oi != xi) or (oj != xj)): 替换dist[xi,xj] = 99999.0obst[xi, xj] = -1toRaise[xi, xj] = 1process[xi, xj] = 1toRaise[i,j] = 0

上面将论文中raise(s)算法中的第17行（原博客Python实现也是与原文献保持一致的）更改如上代码：将if (oi != xi) or (oj != xj): 替换成if (obst[oi, oj] == -1): .。更改后，删除一个障碍物的时间成本由原700ms降低为140ms。

原文献的做法是（和你理解的一样）：一旦障碍物被删除，则将地图中所有不被障碍物占据的格子“格式化”，然后再调用距离传播函数lower(s)重新进行距离传播。
我此处给出的做法是：一旦有障碍物被删除，则只将那些被删除障碍标记的格子“格式化”。当存在多个障碍物时，每个障碍物影响不同区域的栅格。只有那些被删除障碍物标记的格子才需要重新计算距离值。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

如果大家还有更省力的方案，欢迎留言。