基于博弈树的5x5一子棋人机对战

919106840637实验2
这是智能计算三个课程实验的第二个实验，即博弈树搜索 。我之前对博弈树的了解不多，所以实现起来比较的简略，仅仅是基本达到了要求

实验语言

C++

实验内容

实践博弈树搜索——“5x5格子的一字棋问题”，即五子棋，参照课件PPT上的例子来实现。（课件PPT上是3x3）。要求是Max方和Min方都用博弈树来决策，或者一方使用博弈树决策，一方随机或手工走棋，并使用alpha和beta减枝。

实验内容部分我只较好完成了博弈树实现下棋部分，由于博弈树深度较浅，广度也不多，故不剪枝也能拥有较好的性能。剪枝暂时没很好完成，剪枝之后AI貌似~~变蠢了~~ 出了点问题。

实验思想及部分代码

开始照例贴头文件

#include <iostream>
#include <cstdlib>
#include <ctime>
#include <cmath>
#include <cstring>
#include <windows.h>
#include <vector>
#include <algorithm>

完成这个实验我分成了两步

创建一个棋盘
开始下棋

其中第一步非常简单，棋盘直接用一个二维数组即可表示：

int realBoard[5][5];

其中规定，棋盘格的值为0代表空，棋盘格值为1代表AI下在这，棋盘格值为-1代表玩家下在这。

第二步就涉及到下棋的算法了。先简单介绍下博弈树的思想。博弈树就是通过对现有状态进行分析，得到若干个可能的子状态，然后再从若干个子状态出发去分析子状态的子状态…不断迭代就可以形成一棵树。博弈树的概念呢就是这棵树的不同节点会有不同的权值，我们需要根据一定算法去选择最优节点。
在对弈游戏中，轮到自己下时，棋手会将当前棋盘状态当成博弈树的根节点，然后将自己落子不同位置时的棋盘状态当成根节点的子节点，再在此基础上将对手落子不同位置时的棋盘状态当成下一层子节点…可想而知，博弈树的深度越深，棋手考虑的越多越全面。不过过深的博弈树势必会增加计算的时空开销。
除了如何形成一棵博弈树，我们还需要掌握的是如何利用博弈树来选取最佳的落子地点。这里以三层的博弈树为例，即除根节点外，只考虑棋手下一步以及对手下一步的情况。

我们首先要为博弈树中的每个状态附上一个权值，这个权值在不同状况下有不同的含义。在对弈游戏中，可以将权值视为对棋手的有利影响因子，即权值越大，棋手越有可能获胜。在这里很容易想到，棋手希望目标状态的权值越大越好，而对手则希望将权值降到最低。
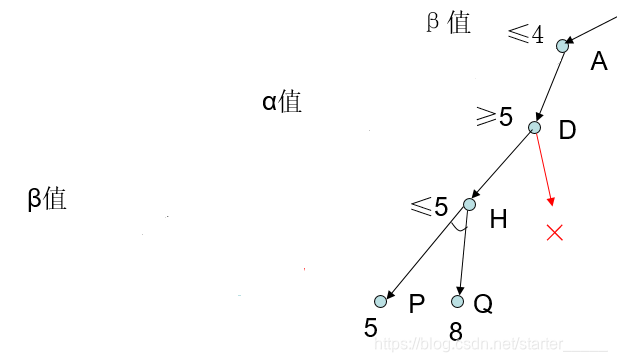
先不去考虑权值h是如何得到的。我们来看看如何得到棋手所期望的最佳状态呢？棋盘当前状态在根节点也就是第一层，棋手期望下一步能够胜率最大，即选取权值最大的第二层状态。而第二层状态的权值可以被第三层的状态权值所影响，即对手下一步不同的下法会影响到棋手上一步的胜率，显而易见如果对手是个世外高人，招招致命，第二层状态的权值就应该等于对应子状态的最小值（对手下棋的目的是让你胜率尽可能小）。一个三层的博弈树就结束了，如果是更深的博弈树，则第三层的权值还要受到棋手进一步下棋即第四层状态的影响，循环往复，这过于复杂所以姑且不论。这个方法叫做极小极大分析法，父状态取该层最大权值的状态层叫MAX层，父状态取该层最小权值的状态层叫MIN层。

在这里插入图片描述

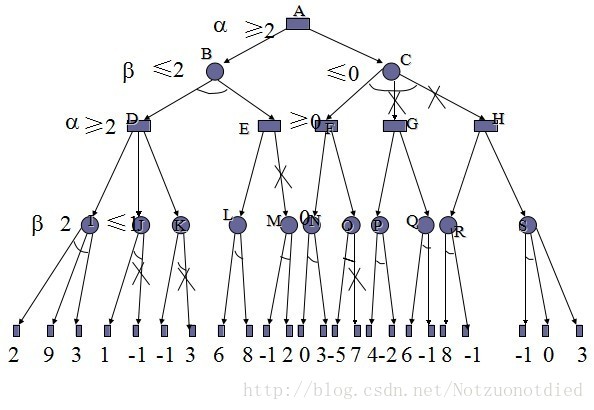
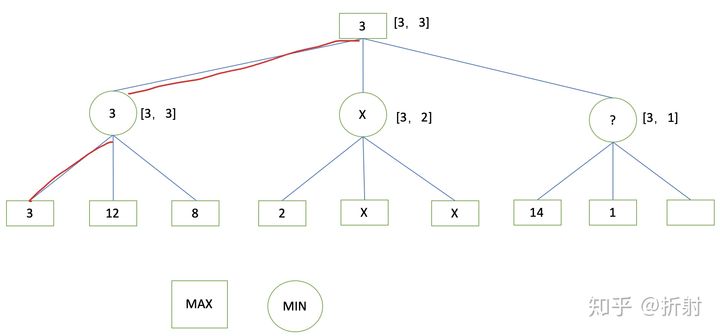
举个例子，如上图。棋手在根节点代表的状态时有三种下法，分别对应三个第二层子状态。棋手想要知道哪种下法更容易赢，就要找到权值最大的子状态。现在对于三个子状态的权值我们还不知道。要求第二层状态的权值，我们就要考虑如果棋手下了这步棋，对手会去怎么下，即分解出第三层的状态。由于第三层是最终层，我们无法通过第四层来获取第三层的权值，所以我们需要利用估值算法来对第三层状态的权值进行估计。通过估值算法求出每个第三层状态权值后，我们就可以选择其中最低的权值作为第二层节点的对应状态的权值（对手肯定不想棋手好过）。然后棋手想要最大胜率，则应该选择权值最大的第二层状态所代表的下法。
自此，棋手就通过简单的三层博弈树算法算出了他下一步该走哪最好。可以说，棋圣的脑子都是计算机，里面装了棵庞大的博弈树用来和对手勾心斗角。
至于上文提到的估值算法，有很多种，我就不赘述了。

然后就贴一贴代码吧。
实现的估值函数

int e(int board[5][5]){	//估值函数int eplus = 0;int eminus = 0;int index_p = 0;int index_m = 0;for(int i=0;i<5;i++){//行index_m = 0;index_p = 0;for(int j=0;j<5;j++){if(board[i][j] == 1) index_p++;else if(board[i][j] == -1) index_m++;}if(index_p == 5){eplus = 9999;break;}else if(index_m == 5){eminus = 9999;break;}else if(index_p != 0 && index_m == 0) eplus+=index_p*index_p;else if(index_m != 0 && index_p == 0) eminus+=index_m*index_m;//列index_m = 0;index_p = 0;for(int j=0;j<5;j++){if(board[j][i] == 1) index_p++;else if(board[j][i] == -1) index_m++;}if(index_p == 5){eplus = 9999;break;}else if(index_m == 5){eminus = 9999;break;}else if(index_p != 0 && index_m == 0) eplus+=index_p*index_p;else if(index_m != 0 && index_p == 0) eminus+=index_m*index_m;}//对角线index_m = 0;index_p = 0;for(int i=0;i<5;i++){if(board[i][i] == 1) index_p++;else if(board[i][i] == -1) index_m++;}if(index_p == 5){eplus = 9999;}else if(index_m == 5){eminus = 9999;}else if(index_p != 0 && index_m == 0) eplus+=index_p*index_p;else if(index_m != 0 && index_p == 0) eminus+=index_m*index_m;//负对角线index_m = 0;index_p = 0;for(int i=0;i<5;i++){if(board[i][4-i] == 1) index_p++;else if(board[i][4-i] == -1) index_m++;}if(index_p == 5){eplus = 9999;}else if(index_m == 5){eminus = 9999;}else if(index_p != 0 && index_m == 0) eplus+=index_p*index_p;else if(index_m != 0 && index_p == 0) eminus+=index_m*index_m;return eplus-eminus;
}

AI下棋逻辑

//AI下棋statue* nowBoard = new statue;for(int i=0;i<5;i++){for(int j=0;j<5;j++){nowBoard->hypoBoard[i][j] = realBoard[i][j];}}//生成所有AI可能的下法(未剪枝)for(int i=0;i<5;i++){for(int j=0;j<5;j++){if(nowBoard->hypoBoard[i][j] == 0){statue* p = new statue;for(int m=0;m<5;m++){for(int n=0;n<5;n++){p->hypoBoard[m][n] = nowBoard->hypoBoard[m][n];}}p->hypoBoard[i][j] = 1;p->max_min = true;p->father = nowBoard;nowBoard->sons.push_back(p);}}}//进一步预测玩家的下法(未剪枝)for(int a=0;a<(int)nowBoard->sons.size();a++){statue* t = nowBoard->sons[a];for(int i=0;i<5;i++){for(int j=0;j<5;j++){if(t->hypoBoard[i][j] == 0){statue* p = new statue;for(int m=0;m<5;m++){for(int n=0;n<5;n++){p->hypoBoard[m][n] = t->hypoBoard[m][n];}}p->hypoBoard[i][j] = -1;p->max_min = true;p->father = t;p->consum = e(p->hypoBoard);t->sons.push_back(p);}}}}//倒推MAX层的代价值for(int a=0;a<(int)nowBoard->sons.size();a++){statue* t = nowBoard->sons[a];int min = 9999;for(int i=0;i<(int)t->sons.size();i++){if(min > t->sons[i]->consum) min = t->sons[i]->consum;}t->consum = min;}//选择模式int max = -9999;int index = -1;for(int a=0;a<(int)nowBoard->sons.size();a++){if(max < nowBoard->sons[a]->consum){max = nowBoard->sons[a]->consum;index = a;}}//下棋for(int i=0;i<5;i++){for(int j=0;j<5;j++){realBoard[i][j] = nowBoard->sons[index]->hypoBoard[i][j];}}//清空指针for(int a=0;a<(int)nowBoard->sons.size();a++){statue* t = nowBoard->sons[a];for(int i=0;i<(int)t->sons.size();i++){delete t->sons[i];}t->sons.clear();delete t;}nowBoard->sons.clear();