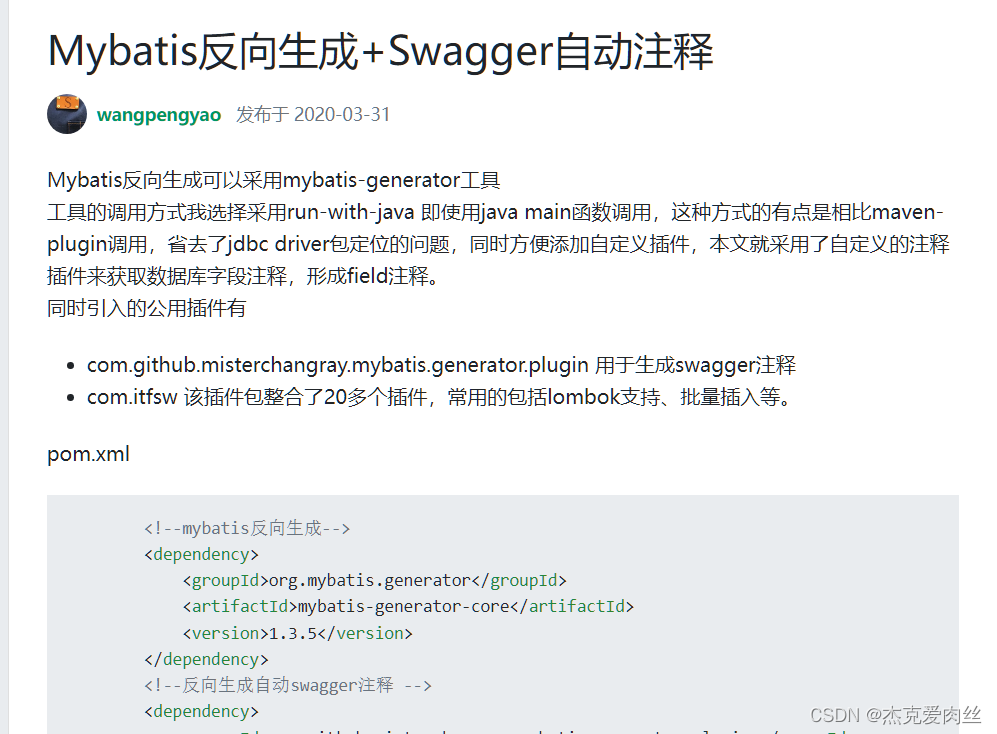
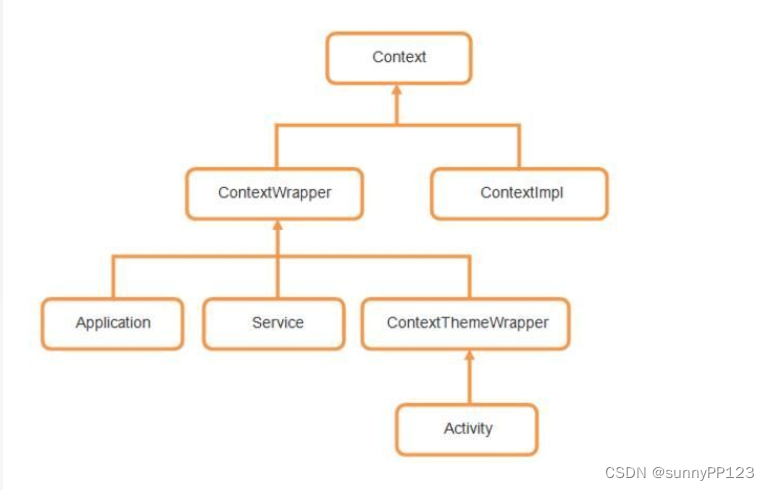
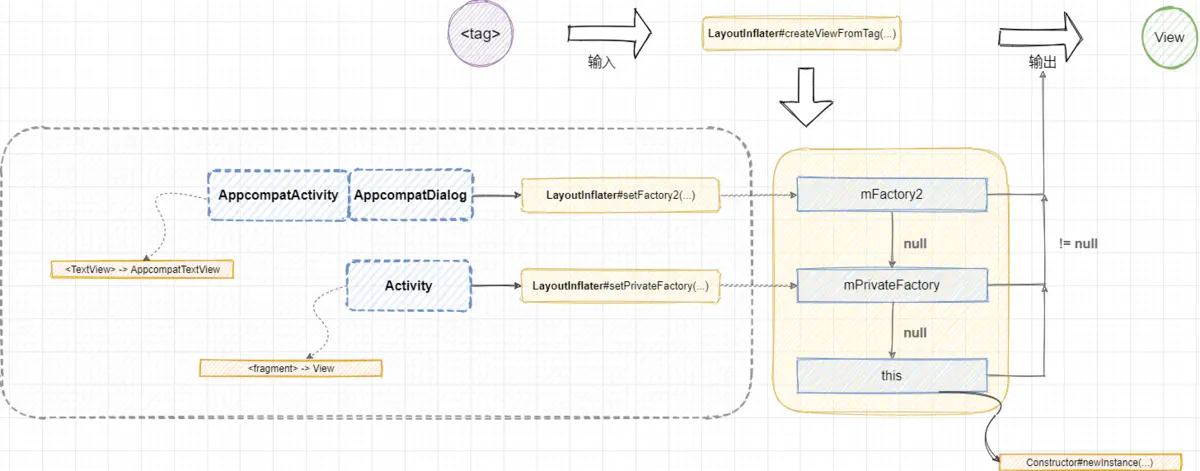
HTML5中canvas标签用于绘制图像(通过脚本,通常是Js)。
也就是说,canvas元素本身没有绘制能力仅仅是图形容 - 您必须使用脚本来完成实际的绘图任务。
getContext() 方法可返回一个对象,该对象提供了用于在画布上绘图的方法和属性。
以下是getContext("2d") 对象的属性和方法:
一、颜色、样式和阴影
| 属性 | 描述 | 值 |
| fillStyle | 设置或返回用于填充绘画的颜色、渐变或模式。 | 默认:#000000;color,gradient,pattern |
| strokeStyle | 设置或返回用于笔触的颜色、渐变或模式 。 | 同fillStyle |
| shadowColor | 设置或返回用于阴影的颜色,必须shadowBlur一起 | 默认:#000000;color |
| shadowBlur | 设置或返回用于阴影的模糊级别。 必须shadowColor一起 | 默认:0;number |
| shadowOffsetX | 设置或返回阴影与形状的水平距离。 | 默认:0,number正负值 |
| shadowOffsetY | 设置或返回阴影与形状的垂直距离。 | 默认:0,number正负值 |
| 方法 | 描述 | 值 |
| createLinearGradient() | 创建线性渐变(用在画布内容上)。 | 参数(x1,y1,x2,y2) |
| createPattern() | 在指定的方向上重复指定的元素。 | (image,"repeat|repeat-x|repeat-y|no-repeat"); |
| createRadialGradient() | 创建放射状/环形的渐变(用在画布内容上) | 参数(x1,y1,r1,x2,y2,r2) |
| addColorStop() | 规定渐变对象中的颜色和停止位置。 | stop:在0.0-1.0之间(stop, color) |
二、线条样式
| 属性 | 描述 | 值 |
| lineCap | 设置或返回线条的结束端点样式 | 默认:butt:末端平直 round:圆形线帽 square:正方形线帽 |
| lineJoin | 设置或返回两条线相交时,所创建的拐角类型。 | 默认:bevel:斜角 round:圆角 |
| lineWidth | 设置或返回当前的线条宽度。 | number:一以像素计 |
| miterLimit | 设置或返回最大斜接长度。 存在lineJoin为miter才有意义 | number:正数 |
解释斜接长度:

三、矩形
| 方法 | 描述 | 参数 |
| rect() | 创建矩形。 | (x,y,width,height) |
| fillRect() | 绘制"被填充"的矩形。默认填充色为黑色,使用fillStyle修改填充色 | (x,y,width,height) |
| strokeRect() | 绘制矩形(无填充)。 默认笔触色为黑色,使用strokeStyle修改填充色 | (x,y,width,height) |
| clearRect() | 在给定的矩形内清除指定的像素 | (x,y,width,height) |
四、路径
| 方法 | 描述 | 参数 |
| fill() | 填充当前绘图(路径) ,填充颜色和fillStyle搭配使用 | 无 |
| stroke() | 绘制已定义的路径。(执行) | 无 |
| beginPath() | 起始一条路径,或重置当前路径。 | 无 |
| moveTo() | 把路径移动到画布中的指定点,不创建线条。 | (x,y)开始坐标 |
| closePath() | 创建从当前点回到起始点的路径。 | 无 |
| lineTo() | 添加一个新点,然后在画布中创建从该点到最后指定点的线条。 | (x,y)结束坐标 |
| clip() | 从原始画布剪切任意形状和尺寸的区域。 | 无 |
| quadraticCurveTo() | 创建二次贝塞尔曲线。 | cpx:贝塞尔控制点的x坐标 cpy:贝塞尔控制点的y坐标 x,y:结束的x,和y坐标 |
| bezierCurveTo() | 创建三次贝塞尔曲线。 | (cpx1,cpy1,cpx2,cpy2,x,y) |
| arc() | 创建弧/曲线(用于创建圆形或部分圆)。 | x,y圆心的坐标 r圆半径 sAngle:起始角 eAngle:结束角 counterclockwise:可选。规定应该逆时针还是顺时针绘图。False = 顺时针,true = 逆时针。 |
| arcTo() | 创建两切线之间的弧/曲线。 | x1,y1:第一条两切线交点的横纵坐标。 x2,y2:第二条两切线交点的横纵坐标。 r:弧半径 |
| isPointInPath() | 如果指定的点位于当前路径中,则返回 true,否则返回 false。 | x,y测试坐标 |
解释二次和三次贝塞尔曲线控制点坐标:


圆参数介绍:


五、转换
| 方法 | 描述 | 参数 |
| scale() | 缩放当前绘图至更大或更小。定位也会被缩放 | scaleWidth,scaleHeight:缩放的宽高 |
| rotate() | 旋转当前绘图 | angle:以弧度计degrees*Math.PI/180 |
| translate() | 重新映射画布上的 (0,0) 位置。 | x,y:横纵坐标 |
| transform() | 替换绘图的当前转换矩阵。 | a:水平缩放绘图 b: 水平倾斜绘图 c:垂直倾斜绘图 d:垂直缩放绘图 e:水平移动绘图 f:垂直移动绘图 |
| setTransform() | 将当前转换重置为单位矩阵。然后运行 transform()。 | 同上 |
六、文本
| 属性 | 描述 | 值 |
| font | 设置或返回文本内容的当前字体属性 | 默认值:10px sans-serif font属性值详细参数见 HTML canvas font 属性 | 菜鸟教程 |
| textAlign | 设置或返回文本内容的当前对齐方式。 | start,end,center,left,right |
| textBaseline | 设置或返回在绘制文本时使用的当前文本基线。 | alphabetic,top,hanging,middle,ideographic,bottom |
| 方法 | 描述 | 参数 |
| fillText() | 在画布上绘制"被填充的"文本。 | text:绘制文本 x,y:位置横纵坐标 maxWidth:可选,最大文本宽度 |
| strokeText() | 在画布上绘制文本(无填充)。 | 同上 |
| measureText() | 返回包含指定文本宽度的对象。 | txt |
七、绘制图像
| 方法 | 描述 | 参数 |
| drawImage() | 向画布上绘制图像、画布或视频。 | (img,x,y);详情参数见 HTML canvas drawImage() 方法 | 菜鸟教程 |
八、像素操作
| 属性 | 描述 | 值 |
| width | 返回 ImageData 对象的宽度。 | |
| height | 返回 ImageData 对象的高度。 | |
| data | 返回一个对象,其包含指定的 ImageData 对象的图像数据。 |  |
| 方法 | 描述 | 参数 |
| createImageData() | 创建新的、空白的 ImageData 对象。 | width:宽度 height:高度 imageData:另一个imageData对象 |
| getImageData() | 返回 ImageData 对象,该对象为画布上指定的矩形复制像素数据。 | x,y:开始复制的左上角位置的 x ,y坐标(以像素计)。 width,height:复制矩形区域的宽高 |
| putImageData() | 把图像数据(从指定的 ImageData 对象)放回画布上。 | (imgData,x,y)参数详情见 HTML canvas putImageData() 方法 | 菜鸟教程 |
九、合成
| 属性 | 描述 | 值 |
| globalAlpha | 设置或返回绘图的当前 alpha 或透明值。 | number:0.0-1.0 |
| globalCompositeOperation | 设置或返回新图像如何绘制到已有的图像上。 | 默认:source_over使用详情见HTML canvas globalCompositeOperation 属性 | 菜鸟教程 |
10、其他

以上属于学习笔记,也就是在学习的过程中把东西敲下来加深印象,具体内容请看下面链接HTML 画布 | 菜鸟教程