各位亲爱的土豪富婆，承蒙您慧眼识珠大驾光临大Y老师为您准备的小灶课堂。

         近期有朋友说发现有人抄袭咱们的文章，自标为“原创”。对此大Y老师有心理准备，咱们的每一篇文章都是大Y老师仔细思考后字斟句酌写下来的，好内容被抄袭已经成了时下难以避免的宿命。不过大Y老师不满意这种做法。抄袭获得非法所得还在其次，主要是这种东抄西抄拼凑的所谓个人网站，内容混乱，无法让读者系统地获得知识，龟玉毁于椟中，最终受伤的是不明真相的读者。前两天看到某院士亲自制作的PPT被某网站以一元一张的价格挂售，不胜唏嘘。知识付费的年代，用钱将知识碎片化了，某种程度上也将知识两头的人割裂开了。

         在此大Y老师向我粉承诺，在咱们公众号阅读原创知识分享，100%永久免费。每期内容会在《生信识图》公众号首发，之后会在知乎/CSDN/微博平台以“生信识图”或“大Y老师”为博主进行宣传。各位大牛关注这个公众号就够了。如果大家愿意，可以“随手一转发，造福你我他”，让更多的大牛们加入进来。如果通过咱们的分享，可以帮助到更多的朋友更好地读懂文献，更好地设计自己的分析，节省大量的时间进行更多的科学探索，将是一件多么幸福的事。

-----以下是日常碎碎念，日理万机的您，可以直接跳到图图图图分割线享用-----

         周六咱们不妨端起一杯可口的饮料，窝在舒服的小角落，一起聊聊风花雪月。不知道各位大牛在实验间歇有没有兴趣采访采访周围的亲朋好友。大Y老师试过，发现在讨论信不信爱情时，真是众说纷纭。咱们不妨来对号入座：

小A：世界上根本就没有爱情，瞎追求什么。到什么年龄干什么事，找个合适的人结婚成家生儿育女，多少代人都是这么过来的，不是也都生活得挺好吗？

小B：世界上可能有爱情吧，但是离我太远了，我这种人是不可能遇到爱情的，我只想搞钱。

小C：爱情？有没有跟我有什么关系呢？我又不在乎，等老子出人头地，少男少女都爱我。

小D：我还是愿意相信这个世界上有爱情，但我年龄也不小了，生活压力比较大，家人朋友都劝我早点成家，我等不起。

小E：爱过。

小F：世界上有爱情，但是爱情这种东西不长久，保鲜期过了，带来的是无尽的腐臭，我想拥有，但又怕付出真心受伤害。

小G：有爱情，我愿意等，我哪也不去就在原地等，直到我命中注定的另一半来叩响我的房门。

小H：有啊，小红、小黄、小兰、小绿、小紫，还有小白和小黑，我都爱过，我还爱小甜、小酸、小苦、小辣，还有个小什么来着我忘记名字了。

小I：我不知道，可能有吧，也可能没有，你们说怎么着就怎么着，我都行。

小J：我老公就爱我啊，虽然他酗酒家暴偶尔pc，但他爱我，他还说等我给他生了儿子就跟我领结婚证。

……

         亲爱的朋友们，打开天窗说亮话，爱情绝对是这个世界上的顶级奢侈品，大多数人类没机会拥有。当然，每个人有绝对的自由选择相信或是不相信，没有对错，甚至没有优劣。不相信爱情的人，这个世界上自有TA们在意和追求的东西，也可以活得恣意潇洒丰富多彩。但是，假如你愿意相信，大Y老师劝你要真信。信和真信是不一样的。小H的信，是信口雌黄的信；小G的信，是迷信；像小D和小F的信，说到底还是不信；至于小J，哪位方便帮她报警吧。

         大Y老师说的真信，是不怀疑、不犹豫、不盲目、也不怯懦。敢迎接、敢追求、敢放弃、也敢接受。信爱情，尤其相信老子值得拥有。不怀疑不犹豫，才能不患得患失，拿爱情和年龄、收入等等反复掂量；不盲目，才能够坚定，慧眼识别真假爱情；不怯懦，才能把主动权掌握在自己手里，而不是一味被动等待怨天尤人。敢迎接，是当有人抛出橄榄枝的时候，愿意以开放的心态接触，给彼此机会；敢追求，是明白自己动心的时候，要不吝表达；敢放弃，是当发现两人之间只是错觉而非真爱的时候，勇于切割；敢接受，不计较寻求真爱时的沉没成本，就算最后没有办法拥有爱情，生活也可以很美好。有了这个心态，大Y老师恭喜您，打败了全球90%的用户。

         不信爱情的人有不信的洒脱，真信爱情的人有真信的精彩。最怕的是好像信又没完全信的人，在洒脱和精彩之间反复磋磨，两头不靠，无尽落寞。

         不知道各位大牛心里是如何看待爱情的呢？如果你愿意选择真信，咱们来聊聊“向内求”的心法。不过，今天碎碎念好像又蛮多了，要不您再琢磨琢磨，我们下次再接着聊？

-----我是图图图图的分割线-----

上次我们一起进阶了PCA的基础。各位大牛还记得重点吗？让我们来自测一下：

         一张PCA plot背后对应的，是多组数据在N个指标上的量，比如说，多个实验组和对照组在两万个基因的表达量；不同个体多个生理指标的测量值。辛苦收集的海量信息，最终缩略到一张只有横纵坐标的散点图上，聪明的你，会不会觉得有点不够？

         你不是一个人。多年来，数学家和生物学家为此动了很多脑筋。给PCA plot增加了许多补充元素，使其可以承载更多的附加价值。让我们打开思路，来看一看PCA plot可以玩出哪些花样：

1. 突破维度的限制

PCA是将多维空间降维到二维或三维空间来展示的过程，人类肉眼最多分辨三维，所以一个PCA plot最多同时展示三条PC轴，也就意味着其他轴所代表的数据差异不能同时展现出来了。于是，组合图就出现了：

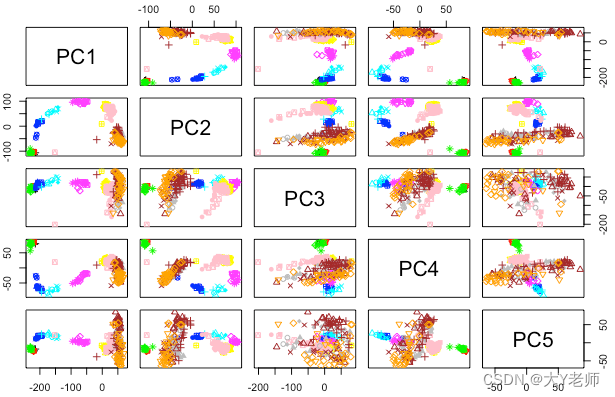
ÅsaBjörklund，NBIS

         在这张图中，展示了PC1-PC5共5条PC轴所有两两组合后的PCA二维图。图中每个点的颜色表示样本分组，可以看到不管选择哪两条PC轴进行组合，降维后的点基本上按照不同颜色，即不同分组分开，证明了组间差异的存在。用这样的图呈现数据质控，是不是比一张二维或三维的PCA plot全面多啦？

2. 增加点的属性

         关注大Y老师《生信识图》公众号的朋友都知道，点的颜色、大小、透明度、形状等等，都是点图的补充元素。我们可以根据实际需要组合使用。比如下面这张PCA plot：

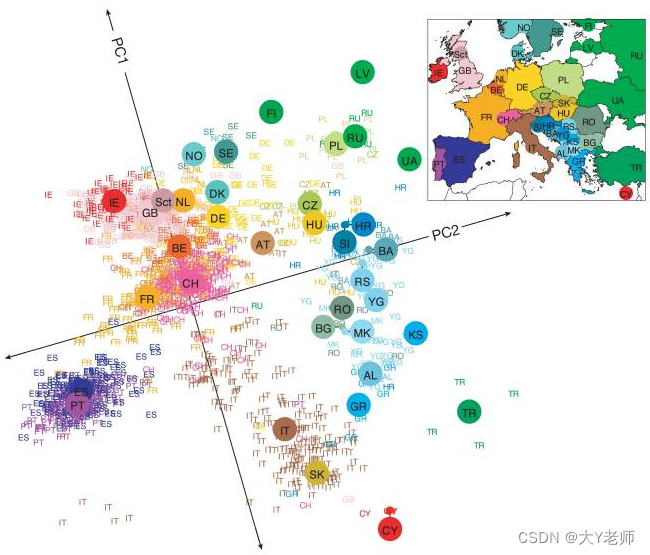
Nature, 2009

         Nature的图果然不同凡响。这张图用PCA plot展示欧洲不同国家共3000个人的genetic variation，即基因组多个位点的序列特征。每个小点（即每一个人）用国家缩写字母代替，用颜色来区分国家和地区。我们可以看到，这些小小的缩写字母基本上按照颜色分开了。作者特别贴心地用一个大圆点来代表同一个国家和地区所有个体在PC1轴和PC2轴的median值，可以想见这个大圆点自然会落在它的人群中心。这样可以帮助读者更清楚地看到不同国家和地区的人总体上是如何分布的。

         如此还不够，在PCA plot的右上角，还加上了欧洲地图，用同样的配色标记国家和地区。值得一提的是，颜色的搭配蛮讲究，从左到右、从上到下，有规律的渐变。而且，为了更好地服务读者，PCA plot图被整体地旋转了一个小角度，使得所有点的分布更匹配欧洲地图的走向，毕竟，图又不是故宫，谁规定必须正南正北地放了。聪明的你能不能想到其他可以加入的补充元素？

3. 再加码，把变量也摆出来

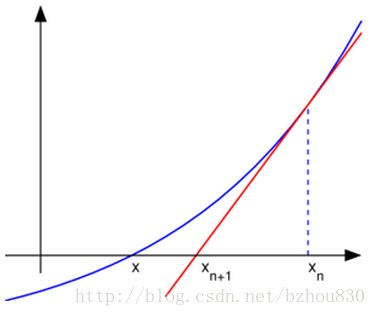
         在前面的讲解中，我们了解到，PCA的轴是为了解释所有点的差异，本身不是具体的变量。那么，我们所测量的真实变量轴有没有办法展示呢？在PCA中，有一个概念叫做loading vector，即一个变量对PC轴的转化系数，也就是我们这个变量与选定的PC轴之间的协同变化程度，大白话类似于，某条PC轴有多像这个变量。比如我们选定用PC1和PC2画PCA plot，那么某一个变量对PC1有一个协同变化系数，对PC2也有一个，那么就可以在这个二维空间中确定一个点。从原点向这个确定的点画出的箭头，就是这个变量在PCA plot中的位置。有几点可以确定的是：

(1).箭头是有方向的，从原点指向坐标点。

(2). 箭头最大值为1，所有变量的loading值都进行了标化处理，因而不同变量的值具有可比性。

(3). 箭头与PC轴的夹角是有意义的，夹角越小，与这条PC轴协同变化程度越高。

(4). 箭头长度也是有意义的，投影到PC轴越长，说明与这条轴协同变化程度越高。

(5). 不同变量箭头之间的夹角也是有意义的，锐角表示两变量间具有正相关性，钝角表示负相关性，直角无相关性。

         带着这几个知识点，我们来一起解读下面这张PCA plot：

Nat Commun.，2020

         哟，PTD这个变量几乎与PC1轴无夹角，说明其对PC1轴所解释的点的差异贡献（下文简称“贡献”）很大，而与PC2轴几乎没什么关系。嗯，PRD这个变量好像比较不偏不倚，在第三象限几乎呈45度角，说明它与PC1和PC2轴都有一定的协同性。而且，别看PTD变量与PC1轴几乎无夹角，PRD在PC1的投影可比PTD还长些，说明PRD对PC1轴贡献更大。不管怎么说，PRD和PTD之间<90度的夹角说明了两个变量之间的正相关性。不过PRD和FM两个变量可就没什么相关性了，二者夹角几乎为90度。

         聪明的你要问了，如果一个变量与PC1和PC2轴协同变化程度都很低呢？那么，这个箭头画出来就会在原点附近。通常我们只会选最大的loading vector展示出来，表明它们是区分这些点最重要的变量。

         上图还贴心地用box plot（箱线图）展示了三组点沿PC1轴和PC2轴的分布情况，以后我们在进阶box plot的时候会详细讲解它的妙用。

4. 这些点到底分几坨呢

         我们一般用颜色、形状等来区分点的不同分组。有没有办法标记出来这些点到底分成几坨呢？有大牛就说了，我画画好，当世达芬奇，我画几个圈圈不就行了。还真不是不行。当点分得比较开的时候，手画几个圈圈是可以的，毕竟谁都能看得出来分成几部分。不过，点多了以后，肉眼终究是要错付了，达芬奇也得伤脑筋。还好PCA还有个隐藏算法可以通过计算点与点之间的距离，区分这些点可以分成几坨，而且提供多种计算距离的统计方法。比如下面这张图：

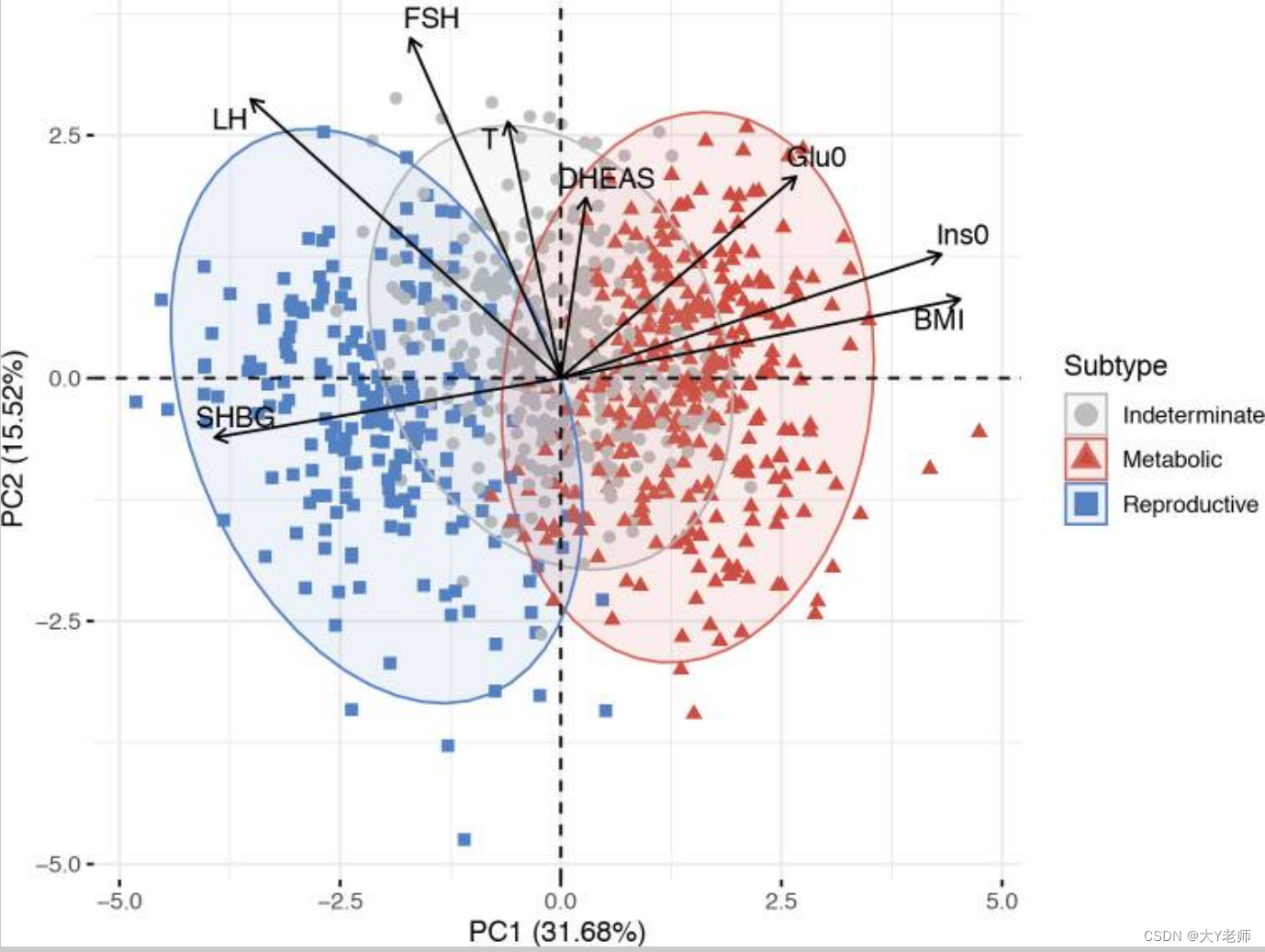
PLoS Med，2020

         三个计算出来的圈基本上按颜色分开了，说明统计出来的结果与实际分组还是比较吻合的。同时聪明的你也会注意到，有一些点不在任何一个圈圈里。它们在当前所选择的统计方法参数下，是outliers。圈圈也不一定都是椭圆形，也可以选择使用不规则的多边形。

         最后，让我们用一张炫酷的PCA plot镇贴。聪明的你能否试试独立解读这张图？

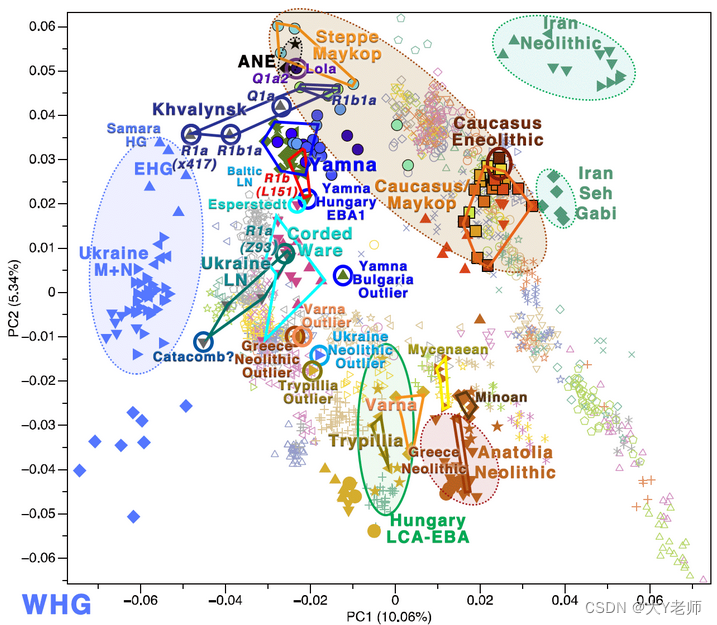
Carlos Quiles， 2018

         PCA的进阶到这里就告一段落啦。我们在PCA plot解读上花了一些时间，因为随着生信进入单细胞时代，“降维”已经成为一个十分重要的概念。理解PCA之后，后续我们可以再上一个台阶，推开单细胞点图的大门。

         读到这里的大牛，一定是好学的好同志，因此大Y老师再赠送你一个彩蛋。我们看到，同样是PCA plot，顶刊与其他期刊的差别体现在哪里呢？有一点很重要的是，顶刊的补充元素特别丰富，图片承载的附加值特别高，于是分析的层次感就更好。跟做人一样有没有？一张PCA plot，无非两条轴一些点；一个人，无非一撇一捺。但是叠上不同的buff之后，不论是图还是人，差距就显现出来了。关注咱们公众号的大牛，有些已经走上工作岗位，有些以后会走上。大家在做好本职工作的基础上，一定要抓住一切机会增加自己的附加价值，努力成为顶刊级别的人。那么，叠buff有什么门道吗？大Y老师给个小建议，如果你从事跟“人”打交道的工作，那么你可以增加跟“物”打交道的附加价值。比如你是做销售的，同时你会修电脑，或者会做视频，那么你就容易突出出来。反过来，如果你从事跟“物”打交道的工作，那么你可以着意增加跟“人”打交道的附加价值，那么你就容易接触到更多机会。像大Y老师每天敲代码做分析，同时喜欢研读周易，喜欢给人看看相啦，算算运势啦，也因此交到许多有趣的朋友，而且成功避开了一些坑。

         好啦，这一期的分享就到这里，让我们步履不停，下期再会。

         欢迎大家关注“生信识图”公众号（shengxinshitu），别忘了点击右上角的···加星标哦，不然后面的精彩推送无法显示（大Y老师也不太理解为什么公众号有这样的设计，请大家包涵啊，手动抱拳）。
         热烈欢迎独一无二的你分享在生信学习中的感想、困扰和乐趣。如果你在阅读文献、图形设计或者恋爱交友、吃喝玩乐方面需要任何咨询，也欢迎给大Y老师私信（评论会看不到，大Y老师也不太理解为什么公众号有这样的设计，请大家包涵啊，手动抱拳），大Y老师最喜欢聊天，期待看到你的消息！