本文是在https://blog.csdn.net/baimafujinji/article/details/89810217基础上增加了自己的理解和解释形成的。
R树的基本情况
R树(R-tree)是一种将B树(B+树和B树统称B树)扩展到多维情况下得到的数据结构,它最初由Antonin Guttman于1984年提出。B树的结点中会存储一个键的集合,这些键把线分成片段,沿着那条线的点仅属于一个片段(B+树中只有叶子节点才存储具体的key和内容,相当于叶子节点把数轴划分的更碎,而内部节点是把这些碎的偏离拼起来,粒度更粗)。因此,B树使得我们可以很容易地找到点。如果把沿线各处的点表示成B树结点,我们就能够确定点所属唯一子结点,在那里可以找到该点。

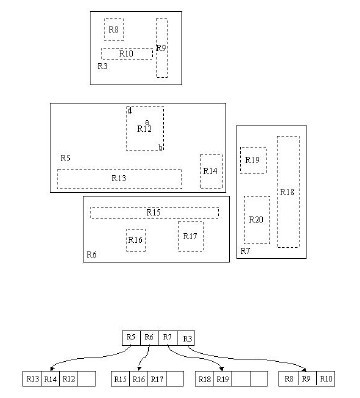
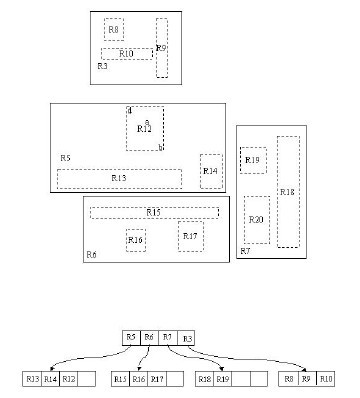
上图是Antonin Guttman在他提出R树的经典论文中给出的R树例子。R树用于组织和管理由二维或者更高维区域组成的数据(可能是多维空间的点,不规则多维形状等),我们把它们称为数据区。一个R树的内部结点对应于整个R树管理的空间内的某个内部区域,或称“区域”,它不是普通的数据区。原则上,区域可以是任意形状,虽然实际中它经常为矩形或其他简单形状。例如上图中(a)是一棵R树,其中的一个内部结点R3、R4、R5就代表(b)中的一个区域,它被包含在R1之中。R树的结点用子区域替代键,子区域表示结点的子结点的内容,例如R3、R4、R5是结点R3、R4、R5中的键,它们中的每一个都表示(b)中的一个子区域。注意,子区域没有覆盖整个区域,只要把位于大区域内的所有数据区都完全包含在某个小区域中就合乎要求。进一步说,子区域允许有部分重叠,例如R3和R4就彼此互有重叠。当然,我们希望重叠的部分尽可能地小。
R树(R-tree)的定义
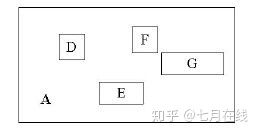
在R-tree中首先要明确的一个概念是Bounding Box (或者简写为BB)。前面已经讲过,区域可以是任意形状,但实际中它经常为矩形,此时我们就将包含有一组对象的一个矩形称为BB。例如上图中的R3就是一个BB,其中包含的对象有R8、R9、R10。再比如,下图中的左图里给出了一组对象,右图中的绿色区域就是一个BB。

在BB的概念之上,还可以定义最小BB(Minimum Bounding Box,MBB),也就是包含一组对象的最小矩形。例如下图中所给出的绿色区域就是一个最小BB。

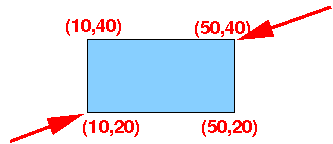
通常可以用一个矩形区域的左下角和右上角的坐标来表示该矩形,例如下面这个矩形就可以表示成((10, 20), (50, 40))。具体来说,对于如何表示一个高维区域,方法很多,对于二维而言,也可以用左下角坐标点与长、宽构成三元组;对于三维,可以用地面的左下角、右上角以及顶面上的任何一个点的三维坐标构成的三元组表示,也可以用立方体的一个顶点加上长宽高构成的四元组表示。对于任何一棵确定的R树,其BB或者MBB的表示也是确定的。
基于上述概念,现在我们终于可以正式地考察R-tree了。R-tree是一种将B树扩展到多维情况下得到的索引树结构。
内部节点
它的内部结点包含了若干条目(entries),这些条目中的每一个都具有如下格式(BB, 指向孩子结点的指针),也就是一个entry = <BB, ptr>,例如:

上图中,BB1指向的那个内部节点有2个entry,分别是BB3和BB4,图中只把1个entry展开了(它没有对其进行命名,我们称之为BB4)。最上层的内部节点中,只是给出了BB1和BB2,实际上是不完整的,那两个entry,每一个都应该还有一个指针,就像BB4那样,只是没有表示出来。
叶子结点
R-tree的叶子结点同样也包含有若干条目,这些条目中的每一个都具有如下格式(MBB, 指向对象的指针),entry = <MBB, ptr> 也就是说叶子结点中包含了指向记录(record)的索引。这里MBB也可以是一个多维坐标点(如物体当做质点处理)。例如:

上图中,上面的黄色节点为内部节点,而下面的绿色为叶子节点,每个叶子节点内有多个entry,左边的叶子节点内部有 2个entry,分别为MBB1和MBB2,其中MBB2展开了。MBB2表示recPtr指向的那个磁盘上的记录(或者数据库中的记录)表示的目标或者物体的大小能用((10,20),(50,40))进行最小表示。放到我们的空间索引上来说,文件记录了飞机的位置或形态,可以用3维坐标(x,y,z)来表示质点或者用容纳飞机轮廓的长方体方体表示(不管是点还是形状,都可以用MBB表示),这些数据存在磁盘文件中的某个位置,我们使用偏移量来表示该record的位置(记录开头的4个字节表示记录的长度)。那么,我们就可以使用MBB和ptr来表征磁盘上的ptr位置存储了一个物体,该物体的位置和轮廓为MBB。
如下图所示,作为一种索引树结构,R-tree的重要性质就是对于一个给定的内部结点中的一个而言,指向孩子结点的指针ptr其实指向了一个对象集合,只不过这些对象必然完全包含在
中。下图中一个内部节点中包含2个entry,entry中的灰色是一个指针,指向下一层的节点。图中的bounding box并不在该内部节点表示,而是放到了其上一层的某个节点的某个entry中表示。

来看一个具体的例子,假设有下面左图所示的一些对象:road1, road2, house1, house2, school, pop, pipeline。现在需要构建一棵R-tree来将这些对象表示出来。首先,如右图所示,road1, road2, house1是完全包含在((0, 0), (60, 50))这个BB中的。

另外,如左图所示,school, pop, house2 和pipeline是完全包含在((20, 20), (100, 80))这个BB中的。如果采用上述这几个BB,那么构建出来的R-tree就如下面的右图所示。

一个重要的注意事项是:R树的结点里使用的BB是可以彼此重叠的(overlap),这一点在本文最开始给出的图示中即有明确的表达,而上面这个刚刚建立的R树的两个内部结点之间也有重叠的部分。
R树中的操作
在R树中进行搜索
这里需要提醒读者的一点是,R树是可以扩展多更高维度情况的,不失普遍性地,这里我们仅以最简单的情况,也就是针对二维的情况来进行讨论。现实中,这也是应用最为广泛的场景。例如,在地图(或者地理信息系统)上进行位置的存储与查询都属于是二维的情况。此时,在R树中进行搜索操作的目的可以是找到一个具体的位置(即一个点)Point(x,y),如果某个叶子所表示的区域中包含了该点,则返回这个叶子,否则就返回空(也就是找不到)。R树的搜索算法是从根开始递归进行的。假设当前结点为n,下面伪代码给出了从此出发递归搜索Point(x,y)的过程。
Lookup( (x, y), n, result )
{// n = current node of the search in the R-treeif ( n == internal node ){for ( each entry ( BB, childptr ) in node n ) do {/* ====================================Look in subtree if (x,y) is in box==================================== */if ( (x,y) ∈ BB ){Lookup( (x,y), childptr, result);}}}else{for ( each object Ob in node n ) do{if ( (x,y) ∈ MBB(Ob) ){Add Ob to result;}}}
}可见,在Lookup函数中:
- 如果n是一个内部结点,那么就逐个搜索其中的条目,如果Point(x,y)被包含在某个条目所给定的BB中,就递归搜索它的孩子。
- 如果n是一个叶子结点,那么就逐个搜索其中的对象,如果Point(x,y)被包含在某个对象的最小BB(MBB)中,则返回该对象作为结果。
搜索点所在的位置
下面来看一个具体的例子,现在的任务是要在前面已经建立好的R树中搜索点P(40,75)。

从根结点开始,因为它不是叶子结点,所以逐个搜索其中的条目,点P(40,75)并不位于((0,0), (60,50))这个BB中,但它位于((20,20), (100,80))这个BB中,所以递归地搜索该子树。如下图所示:
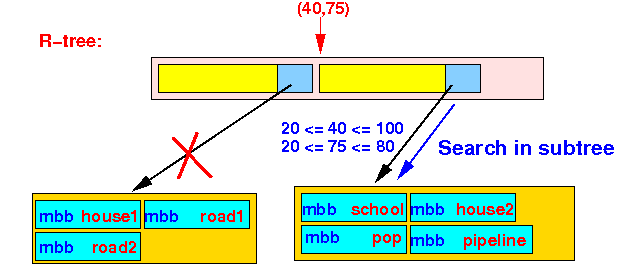
此时,我们已经达到了一个叶子结点,因此逐个搜索其中的对象,发现P(40,75)位于对象school的MBB中,因此最后应该返回该对象作为结果。

搜索区域所在的位置
此外,在R树中进行搜索操作的目的也可以是找到一个对象。这里,我们将问题简化,即用包含该对象的MBB来表示该对象。例如,在下图中,我们要搜索的是一个圆形区域,那么就可以用它的MBB,即((20,50), (45,60)),来表示该对象。
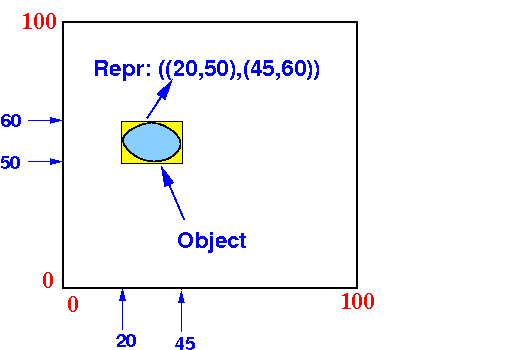
下面来谈一下BB的“包含关系”。假设A是一个BB,它被包含在另外一个记为B的BB中,其充要条件为:
- x_LL(B)≤x_LL(A) 并且 y_LL(B)≤y_LL(A)
- x_UR(A)≤x_UR(B) 并且 y_UR(A)≤y_UR(B)
其中,角标LL表示左下,UR表示右上。下面的图示解释了这种关系,这里不再赘述。
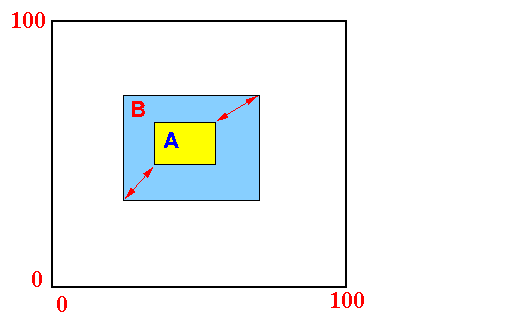
定义了包含关系之后,我们就可以利用R树来进行object搜索了。这里的object是指一小块区域,或者在某个特定位置上的任意形状。这与前面介绍的“在R树中进行点搜索”的算法是一样的。也就是说某个BB包含该object,就递归搜索它的孩子。如果某个最小BB包含该object,则返回表示该BB的对象。
R树在对维数据管理中具有重要应用。在R树被提出之后,又有许多改进型的数据结构被发展处理,例如比较有代表性的Hilbert R树。笔者将会在后续的文章中更加深入地介绍向R树中插入新对象的方法,即R树的插入算法。
参考文献与推荐阅读材料
【1】Hector G. Molina, Jeffrey D. Ullman, Jennifer Widom,数据库系统全书,机械工业出版社
【2】Guttman, Antonin. R-trees: a dynamic index structure for spatial searching. Vol. 14. No. 2. ACM, 1984.
【3】美国埃默里大学Shun Yan Cheung副教授Advanced Database Systems的授课材料(链接)