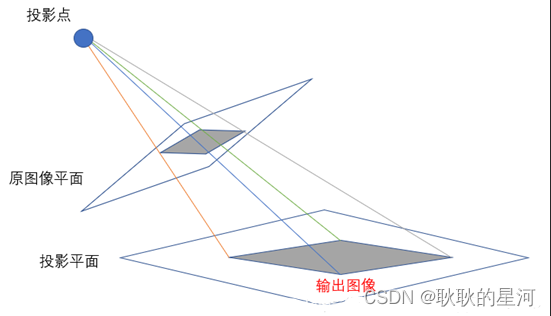
一、透视变换内涵
透视变换本质:将一个图像投影到新的视平面
透视变换思路:
-
将二维坐标系转换为三维坐标系。
-
将三维坐标系投影到新的二维坐标系。
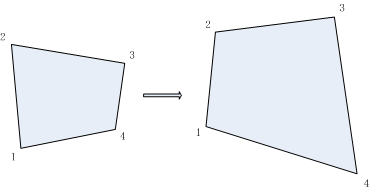
该过程属于非线性变换过程,一个菱形在经过非线性变换后得到一个四边形,但是不在平行。
透视变换又可以称为投影变换,仿射变换属于透视变换的特例。透视变换能够保持直线性,即原图中的直线,在经透视变换后仍为直线。
二、透视变换的详细原理
总体思路:
-
求出投影映射矩阵:根据4个基准坐标对
-
反求出源图像坐标:根据映射矩阵内参数,求一个二元一次方程组
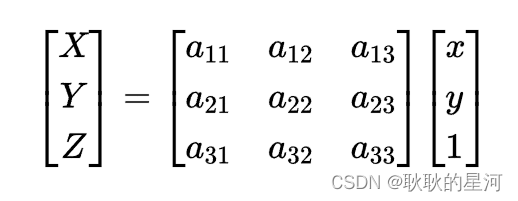
透视变换矩阵变换公式为:
另外定点,即移动到的目标点为:
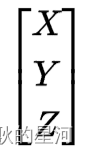
其中透视变换矩阵:

要移动的点,即源目标点(可以手动标记)为:
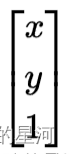
这是一个从二维空间变换到三维空间的转换,因为图像在二维平面,故除以Z,(X’;Y’;Z’)表示图像上的点:
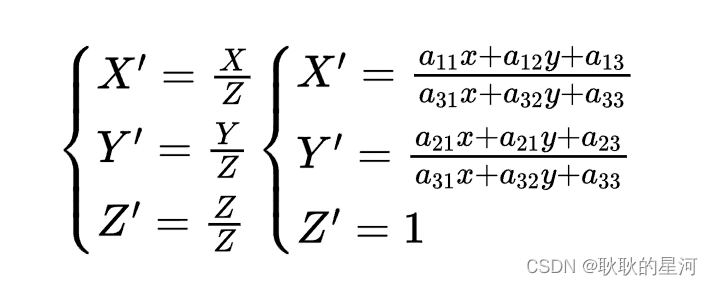
另a33=1,展开上面的公式,可得到一个点为:
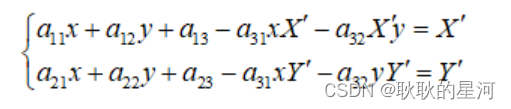
四个点,即可得到8个方程,便可求解出透视变换矩阵A。
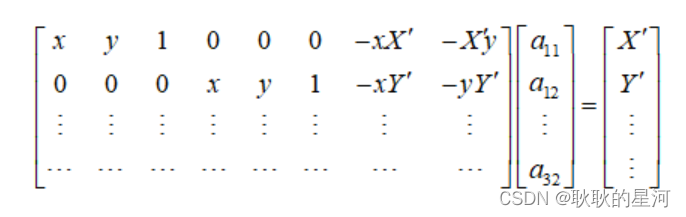
三、Matlab代码实现
clear all;
close all;
clc;img= imread('1.jpg');
img= rgb2gray(img);
imshow(mat2gray(img));
[M N] = size(img);dot=ginput(); %取四个点,依次是左上,右上,左下,右下,这里我取的是书的四个角
w=round(sqrt((dot(1,1)-dot(2,1))^2+(dot(1,2)-dot(2,2))^2)); %从原四边形获得新矩形宽
h=round(sqrt((dot(1,1)-dot(3,1))^2+(dot(1,2)-dot(3,2))^2)); %从原四边形获得新矩形高y=[dot(1,1) dot(2,1) dot(3,1) dot(4,1)]; %四个原顶点
x=[dot(1,2) dot(2,2) dot(3,2) dot(4,2)];%这里是新的顶点,我取的矩形,也可以做成其他的形状
%大可以原图像是矩形,新图像是从dot中取得的点组成的任意四边形.:)
Y=[dot(1,1) dot(1,1) dot(1,1)+h dot(1,1)+h];
X=[dot(1,2) dot(1,2)+w dot(1,2) dot(1,2)+w];B=[X(1) Y(1) X(2) Y(2) X(3) Y(3) X(4) Y(4)]'; %变换后的四个顶点,方程右边的值
%联立解方程组,方程的系数
A=[x(1) y(1) 1 0 0 0 -X(1)*x(1) -X(1)*y(1); 0 0 0 x(1) y(1) 1 -Y(1)*x(1) -Y(1)*y(1);x(2) y(2) 1 0 0 0 -X(2)*x(2) -X(2)*y(2);0 0 0 x(2) y(2) 1 -Y(2)*x(2) -Y(2)*y(2);x(3) y(3) 1 0 0 0 -X(3)*x(3) -X(3)*y(3);0 0 0 x(3) y(3) 1 -Y(3)*x(3) -Y(3)*y(3);x(4) y(4) 1 0 0 0 -X(4)*x(4) -X(4)*y(4);0 0 0 x(4) y(4) 1 -Y(4)*x(4) -Y(4)*y(4)];fa=inv(A)*B; %用四点求得的方程的解,也是全局变换系数
a=fa(1);b=fa(2);c=fa(3);
d=fa(4);e=fa(5);f=fa(6);
g=fa(7);h=fa(8);rot=[d e f;a b c;g h 1]; %公式中第一个数是x,Matlab第一个表示y,所以我矩阵1,2行互换了pix1=rot*[1 1 1]'/(g*1+h*1+1); %变换后图像左上点
pix2=rot*[1 N 1]'/(g*1+h*N+1); %变换后图像右上点
pix3=rot*[M 1 1]'/(g*M+h*1+1); %变换后图像左下点
pix4=rot*[M N 1]'/(g*M+h*N+1); %变换后图像右下点height=round(max([pix1(1) pix2(1) pix3(1) pix4(1)])-min([pix1(1) pix2(1) pix3(1) pix4(1)])); %变换后图像的高度
width=round(max([pix1(2) pix2(2) pix3(2) pix4(2)])-min([pix1(2) pix2(2) pix3(2) pix4(2)])); %变换后图像的宽度
imgn=zeros(height,width);delta_y=round(abs(min([pix1(1) pix2(1) pix3(1) pix4(1)]))); %取得y方向的负轴超出的偏移量
delta_x=round(abs(min([pix1(2) pix2(2) pix3(2) pix4(2)]))); %取得x方向的负轴超出的偏移量
inv_rot=inv(rot);for i = 1-delta_y:height-delta_y %从变换图像中反向寻找原图像的点,以免出现空洞,和旋转放大原理一样for j = 1-delta_x:width-delta_xpix=inv_rot*[i j 1]'; %求原图像中坐标,因为[YW XW W]=fa*[y x 1],所以这里求的是[YW XW W],W=gy+hx+1;pix=inv([g*pix(1)-1 h*pix(1);g*pix(2) h*pix(2)-1])*[-pix(1) -pix(2)]'; %相当于解[pix(1)*(gy+hx+1) pix(2)*(gy+hx+1)]=[y x],这样一个方程,求y和x,最后pix=[y x];if pix(1)>=0.5 && pix(2)>=0.5 && pix(1)<=M && pix(2)<=Nimgn(i+delta_y,j+delta_x)=img(round(pix(1)),round(pix(2))); %最邻近插值,也可以用双线性或双立方插值end end
end
figure;
imshow(uint8(imgn));
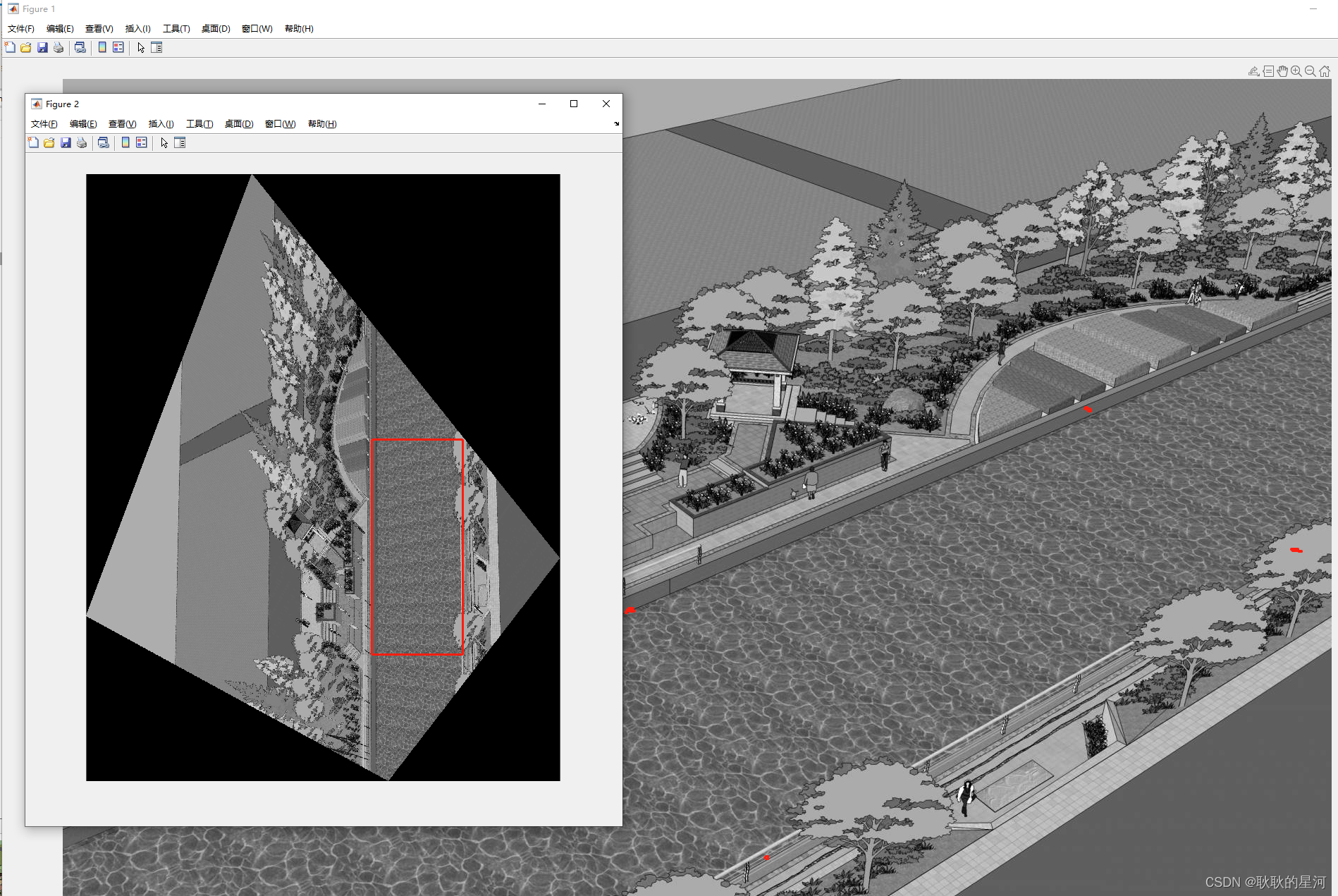
四、效果展示
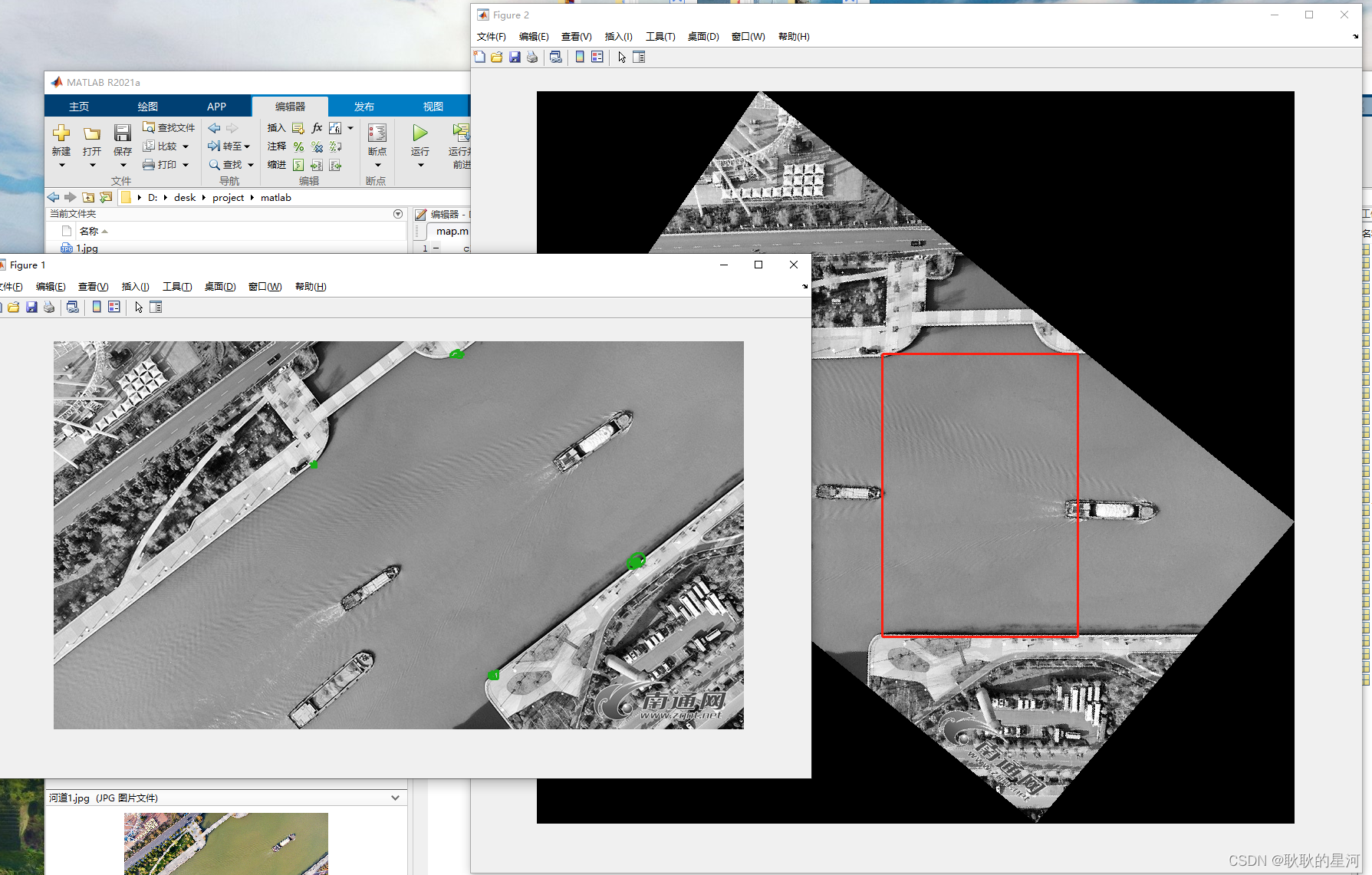










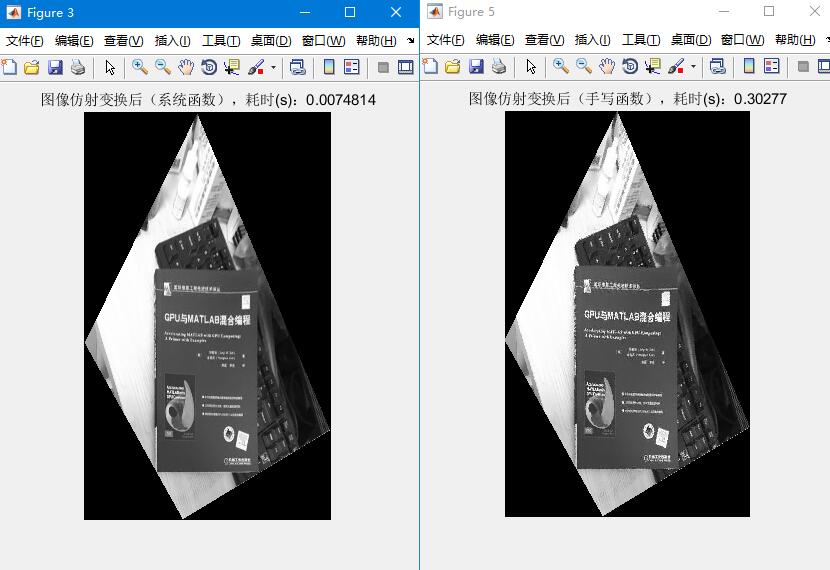


![[解疑]图像、矩阵的二维空间变换](https://img-blog.csdnimg.cn/20200311183346365.png#pic_center)

