3D 空间存在集中变换方式。

1. 欧式变换

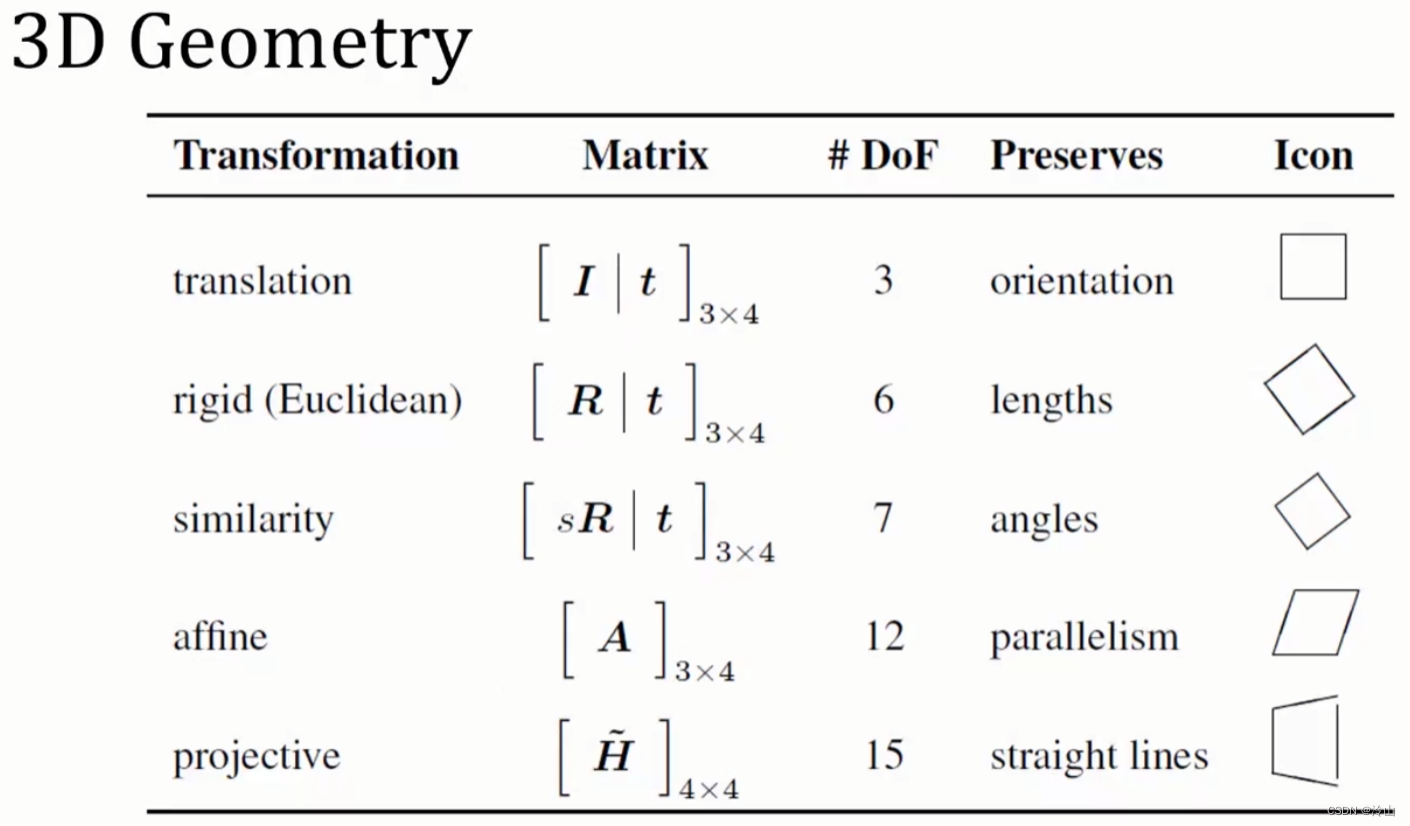
欧式变换保持了向量的长度和夹角，相当于我们把一个刚体原封不动地进行了移动或旋转，不改变它自身的样子，其矩阵表示为：
$${\mathbf{T}}_E=\left[\begin{array}{ll}\mathbf{R}& \mathbf{t}\\ 0^{\mathrm{T}}& 1\end{array}\right]$$

2. 相似变换

相似变换比欧式变换多了一个自由度，它允许物体进行均匀缩放，其矩阵表示为：
$${\mathbf{T}}_S=\left[\begin{array}{ll}s\mathbf{R}& \mathbf{t}\\ 0^{\mathrm{T}}& 1\end{array}\right]$$

注意，旋转部分多了一个缩放因子 $s$，表示我们在对向量旋转之后，可以在 $x,y,z$ 三个坐标上进行均匀缩放。由于含有缩放，相似变换不再保持图形的面积不变。你可以想象一个边长为 $1$ 的立方体通过相似变换后，变成边长为 $10$ 的样子 (但仍然是立方体)。三维相似变换的集合也叫作相似变换群，记作 $\mathrm{Sim}(3)$ 。

3. 仿射变换

仿射变换的矩阵形式如下:
$${\mathbf{T}}_A=\left[\begin{array}{cc}\mathbf{A}& \mathbf{t}\\ 0^{\mathrm{T}}& 1\end{array}\right].$$

与欧式变换不同的是，仿射变换只要求 $\mathbf{A}$ 是一个可逆矩阵，而不必是正交矩阵($R{R}^T=I$)。仿射变换也叫正交投影。经过仿射变换之后，立方体就不再是方的了，但是各个面仍然是平行四边形(自由度：9+3=12)。

4. 射影变换/透视变换

射影变换是最一般的变换，它的矩阵形式为：
$${\mathbf{T}}_P=\left[\begin{array}{ll}\mathbf{A}& \mathbf{t}\\ {\mathbf{a}}^{\mathrm{T}}& v\end{array}\right].$$

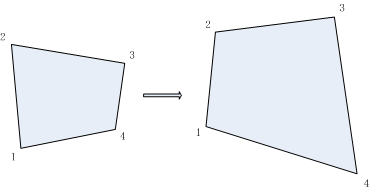
它的左上角为可逆矩阵 $\mathbf{A}$，右上角为平移 $\mathbf{t}$，左下角为缩放 ${\mathbf{a}}^{\mathrm{T}}$。由于采用了齐次坐标，当 $v\ne 0$ 时，我们可以对整个矩阵除以 $v$ 得到一个右下角为 $1$ 的矩阵；否则得到右下角为 $0$ 的矩阵。因此，$2\mathrm{D}$ 的射影变换一共有 $8$ 个自由度，3D 则共有 $15$ 个自由度。射影变换是现在讲过的变换中，形式最为一般的。从真实世界到相机照片的变换可以看成一个射影变换。读者可以想象一个原本方形的地板砖，在照片中是什么样子：首先，它不再是方形的。由于近大远小的关系，它甚至不是平行四边形，而是一个不规则的四边形。

从真实世界倒相机照片的变换是一个射影变换。如果相机的焦距为无穷远，那么这个变换为仿射变换。

概念

透视变换 是指利用透视中心、像点、目标点 三点共线的条件，按透视旋转定律使承影面(透视面)绕迹线(透视轴)旋转某一角度，破坏原有的投影光线束，仍能保持承影面上投影几何图形不变的变换。简而言之，就是将一个平面通过一个投影矩阵投影到指定平面上。

透视是图像中的一种现象，物体距离观察点（例如镜头）越远，看起来就越小，平行的直线在最远处似乎汇聚到同一个点上（vanishing point）。

从数学的角度，我们可以这样描绘透视，在现实世界的 $x,y,z$ 坐标系中，物体 $z$ 坐标值越大，或其与相机的距离越大，它在二维图像中就显得越小。

本质上而言，透视变换改变了对象点的表观 $z$ 坐标，从而改变了该对象的二维图像表示，透视变换扭曲了图像，并有效地将物体推近或推离镜头，以改变表观视角。

例如，我们可以使用透视变换来放大距离较远的物体，这种变换非常有用，因为某些任务，例如计算车道线的曲率，通过图像的鸟瞰图视角要更容易进行。

进行透视变换，需要选择四个点：这些点定义了一个长方形，位于这幅图像的同一平面，四个点就足以确定从一种视角到另一种视角的线性变换了+四个点在变换后出现的位置，变换后的图像被称为扭转图像(wraped image)。

OpenCV 实现

1. 首先在源图像和扭转的目标图像中分别手动创建四个点，这些点可定义透视变换。

2. 透视变换通过一个映射矩阵表示，由 getPerspectiveTransform 函数返回，这个函数接收四个源图像点坐标以及对应的目标图像点坐标，并返回透视变换的映射矩阵。还可以用反向透视变换回复这个图像----只需在这个函数中对调源图像点和目标图像点即可。

M = cv2.getPerspectiveTransform(src, dst)
Minv = cv2.getPerspectiveTransform(dst, src)

3. 接下来，只需对原始图像使用变换矩阵 $M$ 就能得到变换后的扭转图像。这一步调用 wrapPerspective 函数来进行。 这个函数的输入包括源图像、透视矩阵 $M$ 以及想得到的扭转图像的尺寸，此外，扭曲视角还需考虑，如何内插和填充在扭转图像过程中丢失的点

warped = cv2.warpPerspective(img, M, img_size, flags=cv2.INTER_LINEAR)