透视变换
透视变换在比赛中非常重要,我们在地图识别与微调时用到了透视变换。
1. 微调上的使用
在车抵达目标板附件时,摄像头检测到目标板后,可以通过透视变换确定图片距车的位置。这里需要强调下,我们使用的透视变换与四轮使用的有所不同,确切的说是图像坐标到世界坐标的一种变换。
四轮的透视变换是为了使图像更易于判断元素,而在这里是为了得到确切的位置。所以,我们根本不需要对全图进行变换,只要对一个点进行变换。这样的计算量是非常小的。
下面是透视变换的核心代码。
#返回透视矩阵
#XY为世界坐标,UV为相机坐标
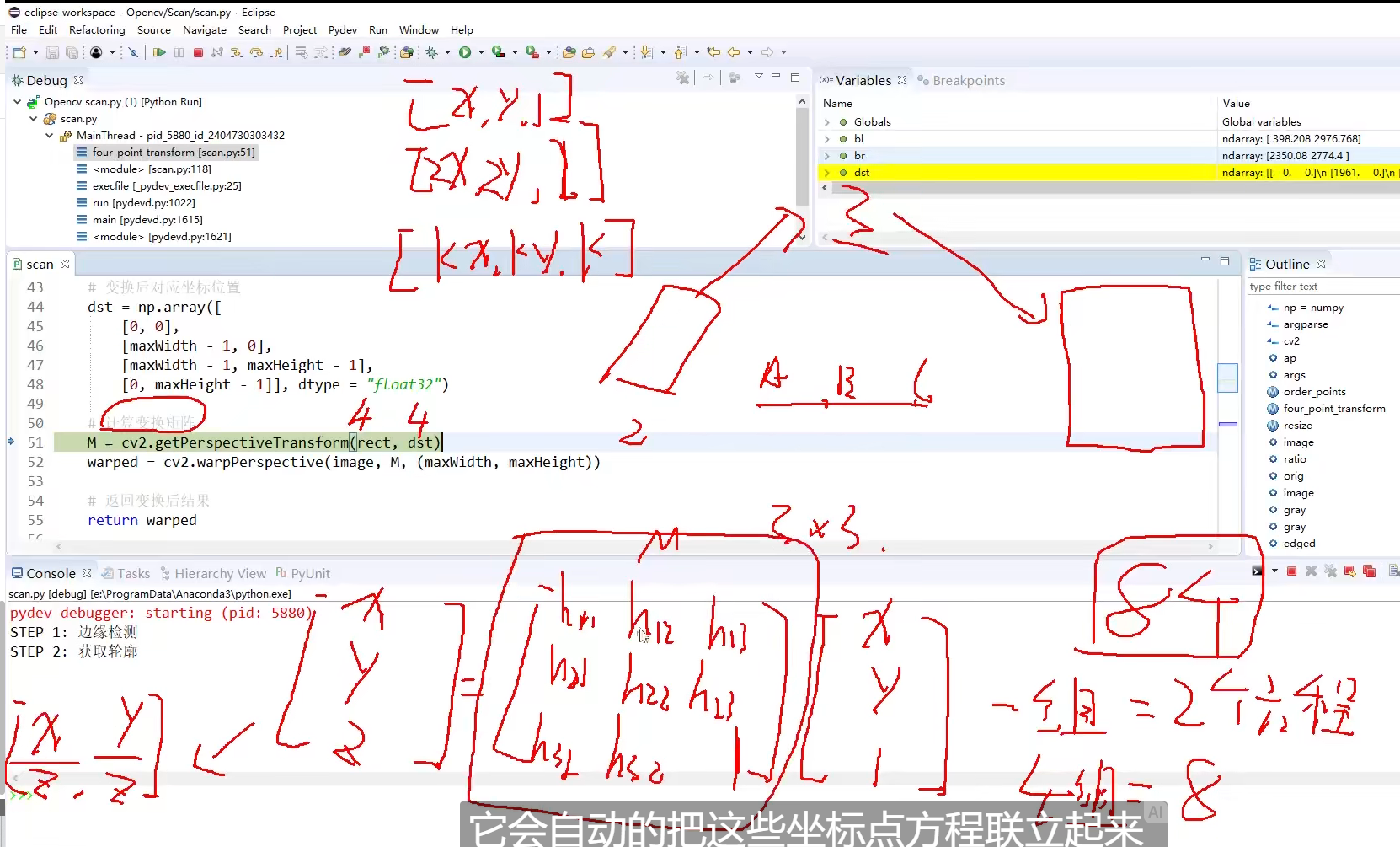
def cal_mtx(UV:np.array,XY:np.array)->np.array:A = []B =[]for i in range(4):a = [[UV[i][0],UV[i][1],1,0,0,0,-XY[i][0]*UV[i][0],-XY[i][0]*UV[i][1]],[0,0,0,UV[i][0],UV[i][1],1,-XY[i][1]*UV[i][0],-XY[i][1]*UV[i][1]]]B+= [[XY[i][0]],[XY[i][1]]]A+=aA = np.array(A)B = np.array(B)x= np.solve(A,B)H = [[x[0][0], x[1][0], x[2][0]],[x[3][0], x[4][0], x[5][0]],[x[6][0], x[7][0], 1]]return np.array(H)
其实只有短短几行,本质上是求解一个 3 × 3 3\times3 3×3的矩阵 H H H:
( H 11 H 12 H 13 H 21 H 22 H 23 H 31 H 32 1 ) \begin{pmatrix} H_{11} & H_{12} & H_{13}\\ H_{21} & H_{22} & H_{23}\\ H_{31} & H_{32} & 1\\ \end{pmatrix} H11H21H31H12H22H32H13H231
共有8个未知数,所以求解这个矩阵需要有4个点。
具体的推导这里就不一一赘述了,毕竟打公式比较累。有兴趣的可以搜下。
得到这个矩阵后,将图像上的点化为其次坐标
( X ′ Y ′ S ) = ( H 11 H 12 H 13 H 21 H 22 H 23 H 31 H 32 1 ) ( U V 1 ) \begin{pmatrix} X^{'}\\ Y^{'}\\ S\\ \end{pmatrix} = \begin{pmatrix} H_{11} & H_{12} & H_{13}\\ H_{21} & H_{22} & H_{23}\\ H_{31} & H_{32} & 1\\ \end{pmatrix} \begin{pmatrix} U\\ V\\ 1\\ \end{pmatrix} X′Y′S = H11H21H31H12H22H32H13H231 UV1
因为是齐次坐标,所以要除与S后才能得到真实位置。
这里提供一个快速确定 H H H的脚本(img2world.py),虽然不太严谨,但是按我们的经验,应付比赛是足够的。
将一张A4纸按如下方式摆放

红线画的是A4纸在摄像头的画面。注意A4纸的底部要与摄像头视野的底部对齐。中线与摄像头视野中线对其。这时候会得到一个矩阵 H H H。
我们暂且将车的左右方向定义为x轴,车头方向为y轴。这个时候你会发现,x轴方向的数据是较为准确的(可以用卷尺测试)。但y轴方向的误差应该是很大的。这是因为我们不知道摄像头视野底部离车的中心距离是多少。所以这里需要在y方向上添加一个平移常数。这里用手测一下就好了。
2. 识别地图
在识别地图中,透视变换特别的关键。这关乎到你的发车速度和识别准确率。
如果没有进行透视变换,通常需要调整好后才能识别地图,而且识别准确率不太准确。但经过透视变换并取整后,其输出基本就是上位机生成的点位,不会有误差。
不同于微调,识别地图的透视矩阵不是固定的,每一帧都需要计算一次,通过地图框的四个顶点确定。









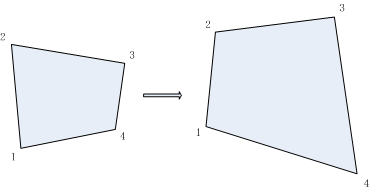


![[解疑]图像、矩阵的二维空间变换](https://img-blog.csdnimg.cn/20200311183346365.png#pic_center)


