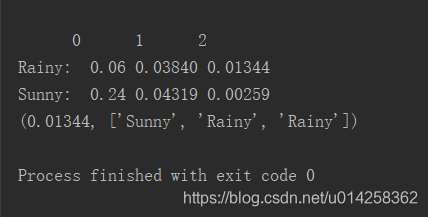
图像畸变矫正——透视变换

article/2025/10/3 21:25:30

图像畸变矫正——透视变换

由于相机制造精度以及组装工艺的偏差引入的畸变，或者由于照片拍摄时的角度、旋转、缩放等问题，可能会导致原始图像的失真，如果要修复这些失真，我们可以通过透视变换，对图像进行畸变矫正。

透视变换的原理推导

透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane)，也称作投影映射(Projective Mapping)。透视变换的目的就是把现实中为直线的物体，在图片上可能呈现为斜线，通过透视变换转换成直线的变换。

仿射变换（Affine Transformation或 Affine Map），又称为仿射映射，是指在几何中，图像进行从一个向量空间进行一次线性变换和一次平移，变换为到另一个向量空间的过程。我们常说的仿射变换是透视变换的一个特例。

以上便是透视变换的原理图，即将源图像通过投影映射，从原图像平面变换到新图像平面。通用的变换公式为：
方程1
(X,Y,Z)是原图像平面坐标点，对应得到变换后的图像平面坐标点为（X’;Y’;Z’），因为我们处理的是二维的图像，所以可以令Z’=1，并将变换后的图像坐标除以Z’，将图片由三维降维为两维，然后可以得到以下方程：
方程2
一般地，我们令a33=1（方便得到X’,Y’，使方程3等号左侧分母为1），展开上面公式，得到一个点的情况：
方程3
方程3中共有8个未知数（aij）,如果要解出该未知数，需要列八组方程，即分别在源图像和目标图像上人为选择四个点（通常选择图片的四个顶点）

在源图像上选四个坐标点，分别为A：（x0,y0),(x1,y1),(x2,y2),(x3,y3)

在目标图像上选四个坐标点，分别为B： (X’0,Y’0),(X’1,Y’1),(X’2,Y’2),(X’3,Y’3)

带入方程3，可以得出方程4，如下：
方程4
使用python，将上述推导过程定义为函数WarpPerspectiveMatrix(src, dst)，计算出变换矩阵warpMatrix，如下：

import numpy as npdef WarpPerspectiveMatrix(src, dst):assert src.shape[0] == dst.shape[0] and src.shape[0] >= 4#assert语句：用以检查某一条件是否为True，若该条件为False则会给出一个AssertionError。#注意这里src和dst的输入并不是图像，而是图像对应的顶点坐标点矩阵。nums = src.shape[0]A = np.zeros((2*nums, 8)) # A*warpMatrix=BB = np.zeros((2*nums, 1))for i in range(0, nums):A_i = src[i,:]B_i = dst[i,:]A[2*i, :] = [A_i[0], A_i[1], 1, 0, 0, 0,-A_i[0]*B_i[0], -A_i[1]*B_i[0]]B[2*i] = B_i[0]A[2*i+1, :] = [0, 0, 0, A_i[0], A_i[1], 1,-A_i[0]*B_i[1], -A_i[1]*B_i[1]]B[2*i+1] = B_i[1]A = np.mat(A)  #创建矩阵#用A.I求出A的逆矩阵，然后与B相乘，求出warpMatrixwarpMatrix = A.I * B #求出a_11, a_12, a_13, a_21, a_22, a_23, a_31, a_32#之后为结果的后处理warpMatrix = np.array(warpMatrix).T[0]   #np.array():创建一个数组，.T[0]：将Tensor进行转置warpMatrix = np.insert(warpMatrix, warpMatrix.shape[0], values=1.0, axis=0) #插入a_33 = 1'''np.insert(arr, obj, values, axis)#arr原始数组，可一可多，obj插入元素位置，values是插入内容，axis是按行按列插入。'''warpMatrix = warpMatrix.reshape((3, 3))return warpMatrixif __name__ == '__main__':'''#一个python文件通常有两种使用方法，第一是作为脚本直接执行，第二是 import 到其他的 python 脚本中被调用（模块重用）执行。# 因此 if __name__ == 'main': 的作用就是控制这两种情况执行代码的过程，在 if __name__ == 'main': 下的代码只有在第一种情况下# （即文件作为脚本直接执行）才会被执行，而 import 到其他脚本中是不会被执行的。'''print('warpMatrix')src = [[10.0, 457.0], [395.0, 291.0], [624.0, 291.0], [1000.0, 457.0]]src = np.array(src)dst = [[46.0, 920.0], [46.0, 100.0], [600.0, 100.0], [600.0, 920.0]]dst = np.array(dst)warpMatrix = WarpPerspectiveMatrix(src, dst)print(warpMatrix)

结果为：

warpMatrix
[[-5.01338334e-01 -1.35357643e+00  5.82386716e+02][-1.38100642e-15 -4.84035391e+00  1.38781980e+03][-2.29650079e-19 -4.14856327e-03  1.00000000e+00]]

上述推导过程是为了，让大家更加直观的的了解透视变换。在实际工程上，opencv库早已将上述过程集成为函数，我们选择网上流行的一张图片校验该opencv库中的畸变矫正算法。

代码块为：

import cv2
import numpy as npimg = cv2.imread('photo1.jpg')result3 = img.copy()#img = cv2.GaussianBlur(img,(3,3),0)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
"""
cv2.Canny(image,            # 输入原图（必须为单通道图）threshold1, threshold2,       # 较大的阈值2用于检测图像中明显的边缘[, edges[, apertureSize[,    # apertureSize：Sobel算子的大小L2gradient ]]])   # 参数(布尔值)：true： 使用更精确的L2范数进行计算（即两个方向的倒数的平方和再开放），false：使用L1范数（直接将两个方向导数的绝对值相加）。
"""
edges = cv2.Canny(gray,50,150,apertureSize = 3)
#cv2.imwrite("canny.jpg", edges)'''
注意这里src和dst的输入并不是图像，而是图像对应的顶点坐标点矩阵。
'''
src = np.float32([[207, 151], [517, 285], [17, 601], [343, 731]])
dst = np.float32([[0, 0], [337, 0], [0, 488], [337, 488]])
# 生成透视变换矩阵；进行透视变换
'''
1 cv2.getPerspectiveTransform(src, dst) → retval参数说明
src：源图像中待测矩形的四点坐标
sdt：目标图像中矩形的四点坐标
返回由源图像中矩形到目标图像矩形变换的矩阵
'''
m = cv2.getPerspectiveTransform(src, dst)       #适用于一组点
'''
cv2.warpPerspective(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) → dst
参数为：
src：输入图像
M：变换矩阵
dsize：目标图像shape
flags：插值方式，interpolation方法INTER_LINEAR或INTER_NEAREST
borderMode：边界补偿方式，BORDER_CONSTANT or BORDER_REPLICATE
borderValue：边界补偿大小，常值，默认为0
'''
result = cv2.warpPerspective(result3, m, (337, 488))  #适用于图片
cv2.imshow("src", img)
cv2.imshow("result", result)
cv2.waitKey(0)