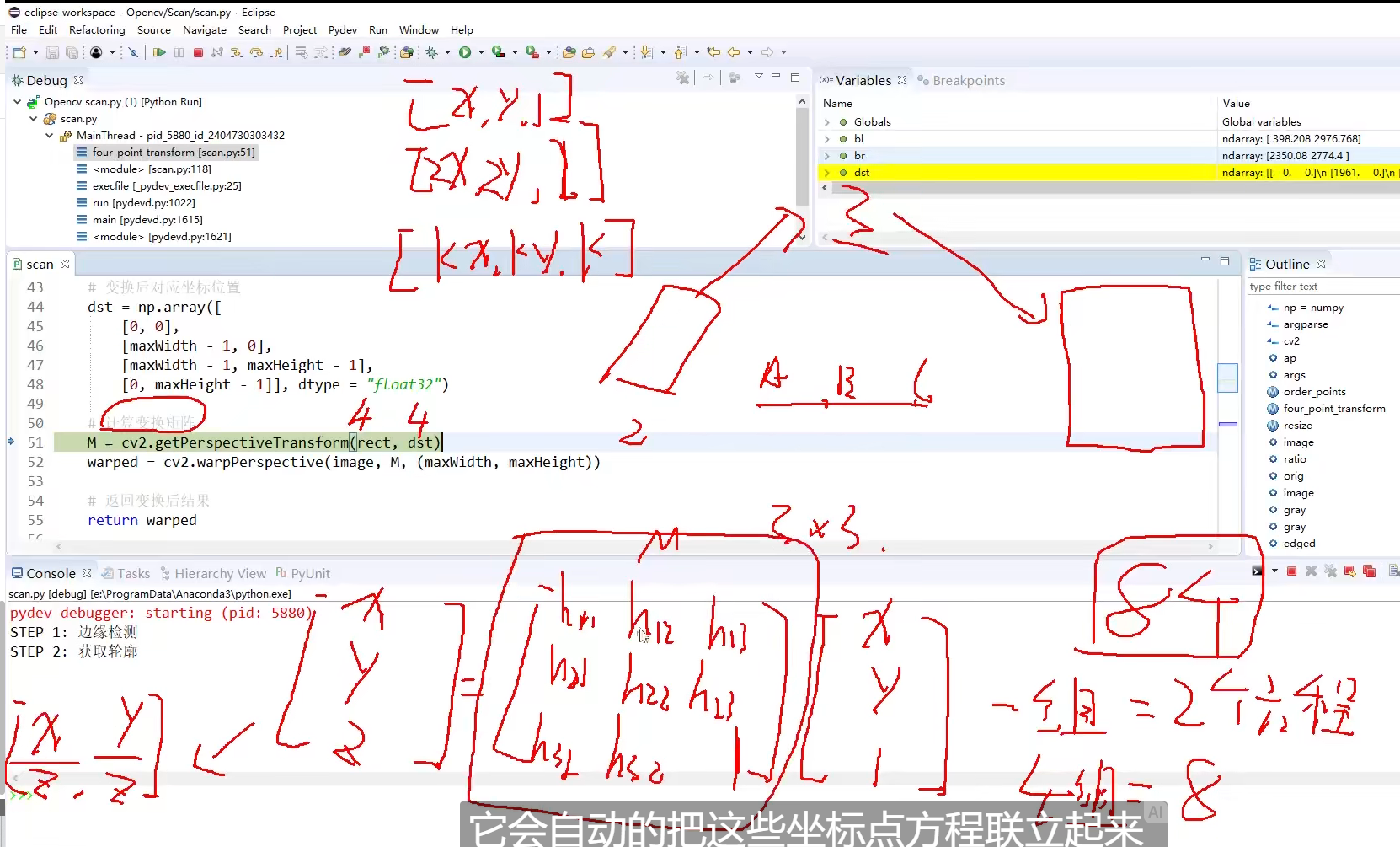
透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plane),也称作投影映射(Projective Mapping)。通用的变换公式为:
u,v是原始图片左边,对应得到变换后的图片坐标x,y,其中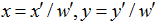
变换矩阵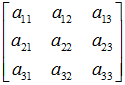
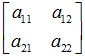
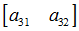
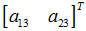
重写之前的变换公式可以得到:
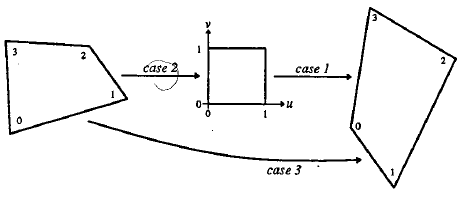
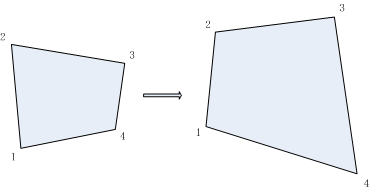
所以,已知变换对应的几个点就可以求取变换公式。反之,特定的变换公式也能新的变换后的图片。简单的看一个正方形到四边形的变换:
变换的4组对应点可以表示成:
根据变换公式得到:
定义几个辅助变量:
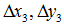
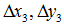
求解出的变换矩阵就可以将一个正方形变换到四边形。反之,四边形变换到正方形也是一样的。于是,我们通过两次变换:四边形变换到正方形+正方形变换到四边形就可以将任意一个四边形变换到另一个四边形。
看一段代码:
PerspectiveTransform::PerspectiveTransform(float inA11, float inA21, float inA31, float inA12, float inA22, float inA32, float inA13, float inA23, float inA33) : a11(inA11), a12(inA12), a13(inA13), a21(inA21), a22(inA22), a23(inA23),a31(inA31), a32(inA32), a33(inA33) {}PerspectiveTransform PerspectiveTransform::quadrilateralToQuadrilateral(float x0, float y0, float x1, float y1,float x2, float y2, float x3, float y3, float x0p, float y0p, float x1p, float y1p, float x2p, float y2p,float x3p, float y3p) {PerspectiveTransform qToS = PerspectiveTransform::quadrilateralToSquare(x0, y0, x1, y1, x2, y2, x3, y3);PerspectiveTransform sToQ =PerspectiveTransform::squareToQuadrilateral(x0p, y0p, x1p, y1p, x2p, y2p, x3p, y3p);return sToQ.times(qToS);
}PerspectiveTransform PerspectiveTransform::squareToQuadrilateral(float x0, float y0, float x1, float y1, float x2,float y2, float x3, float y3) {float dx3 = x0 - x1 + x2 - x3;float dy3 = y0 - y1 + y2 - y3;if (dx3 == 0.0f && dy3 == 0.0f) {PerspectiveTransform result(PerspectiveTransform(x1 - x0, x2 - x1, x0, y1 - y0, y2 - y1, y0, 0.0f,0.0f, 1.0f));return result;} else {float dx1 = x1 - x2;float dx2 = x3 - x2;float dy1 = y1 - y2;float dy2 = y3 - y2;float denominator = dx1 * dy2 - dx2 * dy1;float a13 = (dx3 * dy2 - dx2 * dy3) / denominator;float a23 = (dx1 * dy3 - dx3 * dy1) / denominator;PerspectiveTransform result(PerspectiveTransform(x1 - x0 + a13 * x1, x3 - x0 + a23 * x3, x0, y1 - y0+ a13 * y1, y3 - y0 + a23 * y3, y0, a13, a23, 1.0f));return result;}
}PerspectiveTransform PerspectiveTransform::quadrilateralToSquare(float x0, float y0, float x1, float y1, float x2,float y2, float x3, float y3) {// Here, the adjoint serves as the inverse:return squareToQuadrilateral(x0, y0, x1, y1, x2, y2, x3, y3).buildAdjoint();
}PerspectiveTransform PerspectiveTransform::buildAdjoint() {// Adjoint is the transpose of the cofactor matrix:PerspectiveTransform result(PerspectiveTransform(a22 * a33 - a23 * a32, a23 * a31 - a21 * a33, a21 * a32- a22 * a31, a13 * a32 - a12 * a33, a11 * a33 - a13 * a31, a12 * a31 - a11 * a32, a12 * a23 - a13 * a22,a13 * a21 - a11 * a23, a11 * a22 - a12 * a21));return result;
}PerspectiveTransform PerspectiveTransform::times(PerspectiveTransform other) {PerspectiveTransform result(PerspectiveTransform(a11 * other.a11 + a21 * other.a12 + a31 * other.a13,a11 * other.a21 + a21 * other.a22 + a31 * other.a23, a11 * other.a31 + a21 * other.a32 + a31* other.a33, a12 * other.a11 + a22 * other.a12 + a32 * other.a13, a12 * other.a21 + a22* other.a22 + a32 * other.a23, a12 * other.a31 + a22 * other.a32 + a32 * other.a33, a13* other.a11 + a23 * other.a12 + a33 * other.a13, a13 * other.a21 + a23 * other.a22 + a33* other.a23, a13 * other.a31 + a23 * other.a32 + a33 * other.a33));return result;
}void PerspectiveTransform::transformPoints(vector<float> &points) {int max = points.size();for (int i = 0; i < max; i += 2) {float x = points[i];float y = points[i + 1];float denominator = a13 * x + a23 * y + a33;points[i] = (a11 * x + a21 * y + a31) / denominator;points[i + 1] = (a12 * x + a22 * y + a32) / denominator;}
}int main(){Mat img=imread("boy.png");int img_height = img.rows;int img_width = img.cols;Mat img_trans = Mat::zeros(img_height,img_width,CV_8UC3);PerspectiveTransform tansform = PerspectiveTransform::quadrilateralToQuadrilateral(0,0,img_width-1,0,0,img_height-1,img_width-1,img_height-1,150,250, // top left771,0, // top right0,1023,// bottom left650,1023);vector<float> ponits;for(int i=0;i<img_height;i++){for(int j=0;j<img_width;j++){ponits.push_back(j);ponits.push_back(i);}}tansform.transformPoints(ponits);for(int i=0;i<img_height;i++){uchar* t= img_trans.ptr<uchar>(i);for (int j=0;j<img_width;j++){int tmp = i*img_width+j;int x = ponits[tmp*2];int y = ponits[tmp*2+1];if(x<0||x>(img_width-1)||y<0||y>(img_height-1))continue;uchar* p = img.ptr<uchar>(y);t[j*3] = p[x*3];t[j*3+1] = p[x*3+1];t[j*3+2] = p[x*3+2];}}imwrite("trans.png",img_trans);return 0;
}
另外在OpenCV中也实现了基础的透视变换操作,有关函数使用请见下一篇: 【OpenCV】透视变换 Perspective Transformation(续)
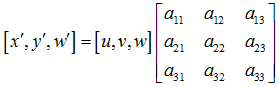
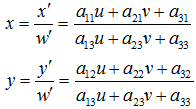
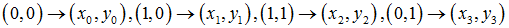
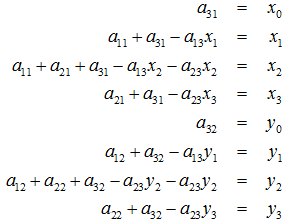
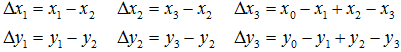
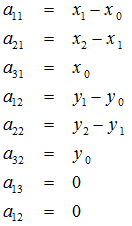
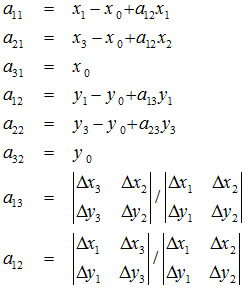







![[解疑]图像、矩阵的二维空间变换](https://img-blog.csdnimg.cn/20200311183346365.png#pic_center)