正态分布(Normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution)
一维正态分布
若 随机变量  服从一个位置参数为
服从一个位置参数为  、尺度参数为
、尺度参数为  的概率分布,且其 概率密度函数为
的概率分布,且其 概率密度函数为
则这个 随机变量就称为 正态随机变量,正态随机变量服从的分布就称为 正态分布,记作  ,读作
,读作  服从
服从  ,或
,或  服从正态分布。
服从正态分布。
μ维随机 向量具有类似的概率规律时,称此随机向量遵从多维正态分布。多元正态分布有很好的性质,例如,多元正态分布的边缘分布仍为正态分布,它经任何 线性变换得到的随机向量仍为多维正态分布,特别它的线性组合为一元正态分布。
标准正态分布
当  时,正态分布就成为 标准正态分布
时,正态分布就成为 标准正态分布

图形特征
集中性:正态曲线的高峰位于正中央,即 均数所在的位置。
对称性:正态曲线以均数为中心,左右对称,曲线两端永远不与 横轴相交。
均匀变动性:正态曲线由均数所在处开始,分别向左右两侧逐渐均匀下降。
曲线与横轴间的面积总等于1,相当于 概率密度函数的函数从正无穷到负无穷积分的概率为1。即频率的总和为100%。  正态分布
正态分布
 正态分布
正态分布 关于μ对称,并在μ处取最大值,在正(负)无穷远处取值为0,在μ±σ处有 拐点,形状呈现中间高两边低,正态分布的概率密度函数 曲线呈钟形,因此人们又经常称之为 钟形曲线。
μ是均值,R里面的mean函数,σ是标准差,sd函数是标准差的平方。
 中的f(x),也就是函数值。正态分布中某个满足正太分布变量x的出现概率,即正态分布概率函数
中的f(x),也就是函数值。正态分布中某个满足正太分布变量x的出现概率,即正态分布概率函数
pnorm(), Probability的缩写,表示概率函数。举个例子,标准正太分布从负无穷大到0的概率,可以用pnorm(0)计算,就是正太曲线跟x轴围成的面积。对  在区域(x,y)上面的积分。
在区域(x,y)上面的积分。
qnorm(), Quantile的缩写,表示分位函数。举个例子,如果知道标准正太分布从负无穷大到x的概率是0.9678,想要知道这个x的值,可以通过qnorm(0.9678)计算,其实就是对pnorm的逆解,对 pnorm函数求导的结果,得到概率所对应的分位数,即  在x轴上围成区域面积所得概率的x域(x,y)的解。
在x轴上围成区域面积所得概率的x域(x,y)的解。
rnorm(n, mean=0, sd=1)
r Random的缩写,表示随机函数。用于随机生成符合正太分布的数值,举个例子,如果想随机生成10个符合标准正太分布的函数,可以用rnorm(10)来获得。
μ是均值,R里面的mean函数,σ是标准差,sd函数是标准差的平方。
参数含义
正态分布有两个参数,即期望(均数)μ和标准差σ,σ^2为方差。  正态分布公式
正态分布公式
 正态分布公式
正态分布公式 正态分布具有两个参数μ和σ^2的 连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的 均值,第二个参数σ^2是此随机变量的 方差,所以正态分布记作N(μ,σ^2)。
μ是正态分布的位置参数,描述正态分布的 集中趋势位置。概率规律为取与μ邻近的值的概率大,而取离μ越远的值的概率越小。正态分布以X=μ为 对称轴,左右完全对称。正态分布的期望、 均数、 中位数、众数相同,均等于μ。
σ描述正态分布资料数据分布的离散程度,σ越大,数据分布越分散,σ越小,数据分布越集中。也称为是正态分布的形状参数,σ越大,曲线越扁平,反之,σ越小,曲线越瘦高。
在  时,正态分布就成为 标准正态分布。
时,正态分布就成为 标准正态分布。
在R中,rnorm()函数来随机抽取正太分布随机数,只是抽取符合正态分布的随机数,就是
dnorm为正态分布的概率密度函数,就是 面积分布
1.实际工作中,正态曲线下横轴上一定区间的面积反映该区间的例数占总例数的百分比,或变量值落在该区间的概率(概率分布)。不同 范围内正态曲线下的面积可用公式计算。
⒉正态曲线下, 横轴区间(μ-σ,μ+σ)内的面积为68.268949%。
P{|X-μ|<σ}=2Φ(1)-1=0.6826
横轴区间(μ-1.96σ,μ+1.96σ)内的面积为95.449974%。
P{|X-μ|<2σ}=2Φ(2)-1=0.9544
横轴区间(μ-2.58σ,μ+2.58σ)内的面积为99.730020%。 [2]
P{|X-μ|<3σ}=2Φ(3)-1=0.9974
由于 “小概率事件”和 假设检验的基本思想 “小概率事件”通常指发生的概率小于5%的事件,认为在一次试验中该事件是几乎不可能发生的。由此可见X落在(μ-3σ,μ+3σ)以外的概率小于千分之三,在实际问题中常认为相应的事件是不会发生的,基本上可以把区间(μ-3σ,μ+3σ)看作是随机变量X实际可能的取值区间,这称之为正态分布的“3σ”原则。
在
在R中,rnorm()函数来随机抽取正太分布随机数,只是抽取符合正态分布的随机数,就是  中的x向量集合
中的x向量集合

rnorm(n, mean = 0, sd = 1)##有三个参数
n 为产生随机值个数(长度),mean 是平均数, sd 是标准差 。
使用该函数的时候后,一般要赋予它 3个值.
rnorm() 函数会随机正态分布,然后随机抽样 或者取值 n 次,
>rnorm(5,0,1) 以N(0,1)的正态分布,分别列出5个值。
r 这列代表随机,可以替换成dnorm, pnorm, qnorm 作不同计算
r = random = 随机, d= density = 密度, p= probability = 概率 , q=quantile = 分位
pnorm(), Probability的缩写,表示概率函数。举个例子,标准正太分布从负无穷大到0的概率,可以用pnorm(0)计算,就是正太曲线跟x轴围成的面积。对
qnorm(), Quantile的缩写,表示分位函数。举个例子,如果知道标准正太分布从负无穷大到x的概率是0.9678,想要知道这个x的值,可以通过qnorm(0.9678)计算,其实就是对pnorm的逆解,对 pnorm函数求导的结果,得到概率所对应的分位数,即
rnorm(n, mean=0, sd=1)
r Random的缩写,表示随机函数。用于随机生成符合正太分布的数值,举个例子,如果想随机生成10个符合标准正太分布的函数,可以用rnorm(10)来获得。
dnorm(x,mean = 0, sd = 1, log = FALSE)
d Density的缩写,表示密度函数。举个例子,标准正太分布x=0对应的值可以用dnorm(0)计算
pnorm(q,mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
p Probability的缩写,表示概率函数。举个例子,标准正太分布从负无穷大到0的概率,可以用pnorm(0)计算
qnorm(p,mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
q Quantile的缩写,表示分位函数。举个例子,如果知道标准正太分布从负无穷大到x的概率是0.9678,想要知道这个x的值,可以通过qnorm(0.9678)计算。


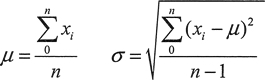

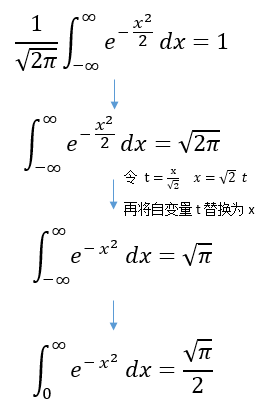







![[基础]-向量点乘和叉乘](https://img-blog.csdnimg.cn/8860a56daa704873b54c8e05ffa8e076.png)
