向量的点乘(内积、数量积)和叉乘(外积、向量积)

文章目录

• 向量的点乘(内积、数量积)和叉乘(外积、向量积)
• • @[TOC]
  • • 0.绪论
    • 1.向量点乘（内积）
    • • 1.代数角度看
      • 2.从几何方面看
      • 3.常用公式：
    • 2.向量叉乘(外积)
    • • 1.代数角度看：
      • 2.几何角度看：
    • 3.总结

0.绪论

总是遇到向量点乘和叉乘之间的计算，总是傻傻的分不清楚理解不了点乘和叉乘之间代表的几何意义，今天写这篇文章来总结下点乘和叉乘加深映像，以个人比较容易理解的方式写。另外就是看了网上一些文章符号和图片不对应，有些看着看着多出来一些新符号也没用解释新符号的定义。看起来特别吃力让人抓狂，所以打算自己写一点。

1.向量点乘（内积）

点乘又称为点积、数量积或者标量积。(它的结果是一个数、一个标量)

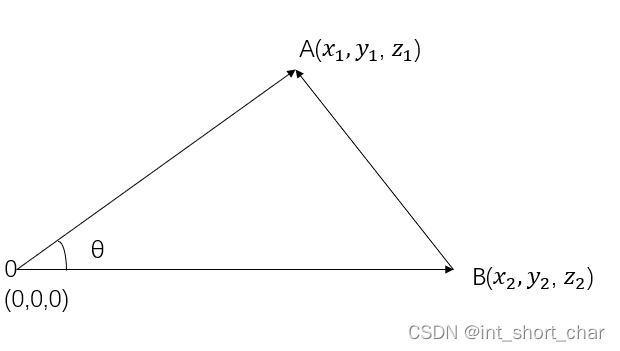
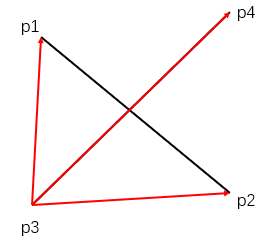
此处声明一下向量定义，后面就用向量$\overrightarrow{a}$表示$\overrightarrow{OA}$，向量$\overrightarrow{b}$表示$\overrightarrow{OB}$，$\overrightarrow{c}$表示$\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{BA}$。
$\overrightarrow{a}=(x_1,y_1,z_1),\overrightarrow{b}=(x_2,y_2,z_2),\overrightarrow{c}=(x_2-x_1,y_2-y_1,z_2-z_1)$
向量$\overrightarrow{a}和\overrightarrow{b}$之间的夹角为$\theta$。

1.代数角度看

点积是对两个向量对应位置上的值相乘再相加的操作。即：
$\overrightarrow{a}\cdot \overrightarrow{b}=x_1{x}_2+y_1{y}_2+z_1{z}_2....①$是一个数）

2.从几何方面看

$\overrightarrow{a}\cdot \overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos\theta$
表示的是两个向量的长度和他们之间夹角的余弦的乘积。
即：
点乘的结果表示向量$\overrightarrow{a}$在向量$\overrightarrow{b}$方向上的投影的长度与$|\overrightarrow{b}|$的乘积。它反映了向量在方向上的相似程度。{举个例子：假设向量$\overrightarrow{a}$和$\overrightarrow{b}$都是单位向量那么$\overrightarrow{a}.\overrightarrow{b}=cos(\theta )$ 两个向量的点积可以分为三种情况来看：1.$\overrightarrow{a}.\overrightarrow{b}=1$(表示此时两个向量方向相同)；2.$\overrightarrow{a}.\overrightarrow{b}=0$(此时表示两 个向量相互垂直)；3.$\overrightarrow{a}.\overrightarrow{b}⪇0$（表示两个向量方向相反）}

3.常用公式：

$\overrightarrow{a}\cdot \overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos\theta$…①
$\theta =\arccos (\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|})$…②

2.向量叉乘(外积)

1.代数角度看：

$\overrightarrow{a}\times \overrightarrow{b}=(y_1{z}_2-z_1{y}_2，z_1{x}_2-x_1{z}_2，x_1{y}_2-y_1{x}_2)$

2.几何角度看：

$\overrightarrow{a}\times \overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\sin \theta \overrightarrow{n}$
这里的向量$\overrightarrow{n}$表示的是$\overrightarrow{a}$和$\overrightarrow{b}$所构成的平面的单位法向量,其结果与这两个都垂直：

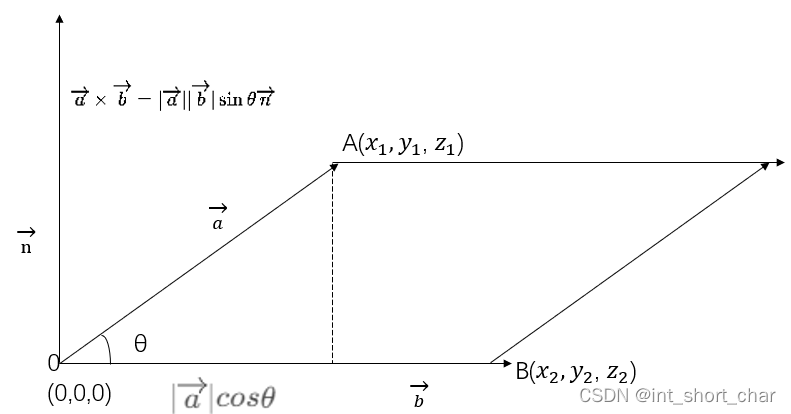
外积向量的大小与$\overrightarrow{a}$和$\overrightarrow{b}$所构成的平行四边形的面积相等，方向与这个平行四边形平面相互垂直。
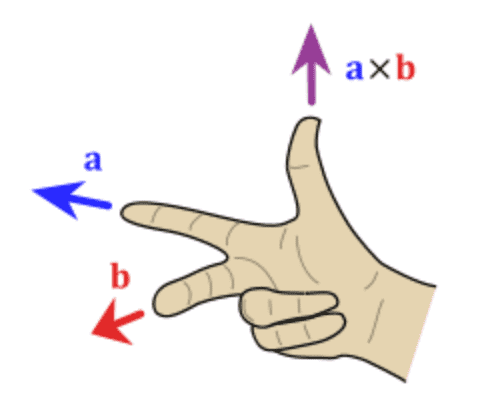
判断叉乘方式，采用右手定则：

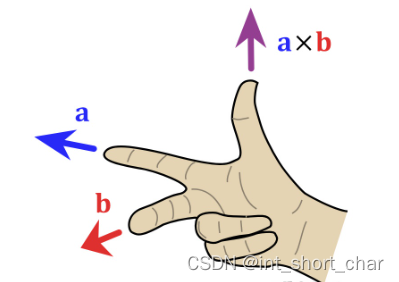
3.总结

点乘反映的是两个向量在方向上的相似度，仅仅是在方向上的相似度（当然强行说长度的相似度也可以，四边形相同周长正方形面积最大）结果越大方向相似度越高。
叉乘求的是两个向量组成的平行四边形面积相等的且和这两个向量垂直的向量，在很多应用中用来求误差。（例：陀螺仪姿态解算求陀螺仪角速度积分与加速度计算的方向叉乘等于偏差）

感谢您的阅读 欢迎指，正共同进步