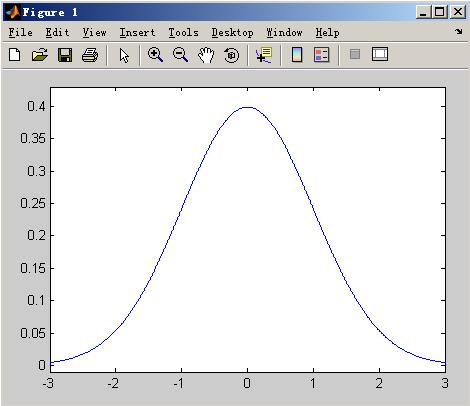
1)使用MatLab画出正态分布的概率密度函数图像。
x=[-10:0.01:10];
y=normpdf(x,0,1);%正态分布函数。
figure;
axes1=axes('Pos',[0.1 0.1 0.85 0.85]);
plot(x,y);
set(axes1,'YLim',[-0.01 0.43],'XLim',[-3 3]);
图1:
2)验证概率密度函数在区间(-∞,∞)上的积分为1。
这里取参数mu=3,sigma=5(注:下文全用这两个参数)。
y='exp(-1/2*((x-3)/5)^2)/(sqrt(2*pi)*5)';
s=int(y,-inf,inf) %int积分函数(inf代表无穷大)。
输出:s=1
3)验证x=mu时取最大值。
思路:求解函数一阶导数为零的点。
* 求一阶导数
y='exp(-1/2*((x-3)/5)^2)/(sqrt(2*pi)*5)';
d=diff(y);%微分函数。
sd=simplify(d)
输出结果:sd = -1/250*(x-3)*exp(-1/50*(x-3)^2)*2^(1/2)/pi^(1/2)
* 通过图像判断解的位置
x=[0:0.001:40];
sd=-1/250.*(x-3).*exp(-1/50.*(x-3).^2).*2.^(1/2)./pi.^(1/2);
axes1=axes('Pos',[0.1 0.1 0.85 0.85]);
plot(x,sd);
set(axes1,'YLim',[-0.01 0.01],'XLim',[0 40]);
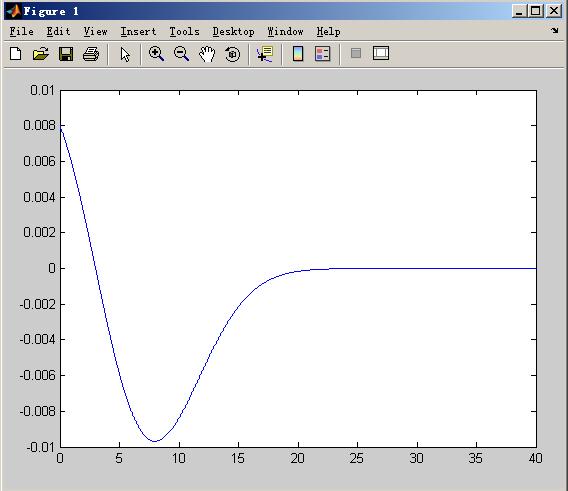
图2:
从图中可以看出在3附近有解。
* 定义函数并求解
function y=f(x)
y=-1/250.*(x-3).*exp(-1/50.*(x-3).^2).*2.^(1/2)./pi.^(1/2);
r=fzero('f',3)
输出:r=3
从图上看在x > 20以后,几乎是一条直线,若用20:
r=fzero('f',20)
输出:r=3
这说明是无限趋近于0。
* 进一步说明该点为最大值点
该概率密度函数一阶导数为0的解为3,此值正好为mu,再取x=1,x=4与x=3时的函数值比较。
>> normpdf(1,3,5)
ans = 0.0737
>> normpdf(4,3,5)
ans = 0.0782
>> normpdf(3,3,5)
ans = 0.0798
显然在x=3的两边函数值都比x=3小,说明该点为极大值点。根据正态分布函数的图像特点可知该点是最大值点。
4)验证x=mu +- sigma (即8或-2)处曲线有拐点。
思路:求二阶导数为零的点。
* 先求二阶微分
y='exp(-1/2*((x-3)/5)^2)/(sqrt(2*pi)*5)';
d=diff(y,2);%微分函数。
sd=simplify(d)
输出:sd = 1/6250*exp(-1/50*(x-3)^2)*2^(1/2)*(-16+x^2-6*x)/pi^(1/2)
* 通过图像判断解的位置
x=[-20:0.001:20];
sd=1./6250.*exp(-1/50.*(x-3).^2).*2.^(1/2).*(-16+x.^2-6.*x)/pi.^(1/2);
axes1=axes('Pos',[0.1 0.1 0.85 0.85]);
plot(x,sd);
set(axes1,'YLim',[-0.005 0.005],'XLim',[-20 20]);
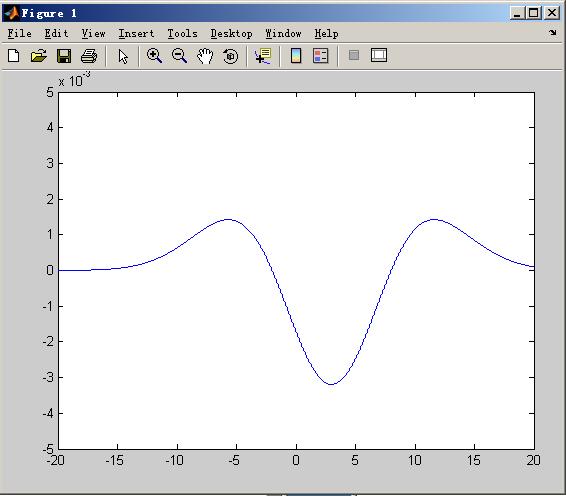
图3:
从上图可以看出,曲线在(-5,0)和(5,10)之间分别都与y=0有交点,因此有两个解。
* 定义函数并求解
function y=f(x)
y=1./6250.*exp(-1/50.*(x-3).^2).*2.^(1/2).*(-16+x.^2-6.*x)/pi.^(1/2);
r=fzero('f',-5)
r = -2
>> r=fzero('f',5)
r = 8.0000
从而得到了两个拐点x=8和x=-2,也即mu +- sigma。
5)验证曲线以x轴为渐近线渐近线求解:
A 垂直渐近线 x=a是y=f(x)的渐近线<==>lim f(x)=∞或lim f(x)=∞
x->a+0 x->a-0
其中a在间断点中找——∞型第二类间断点B 水平渐近线
x→+∞(-∞)时,y=b是y=f(x)的渐近线<==>lim f(x)=b (或lim f(x)=b)
x->+∞ x->-∞
求其一阶倒数在x趋向于无穷大时的极限值b,若存在,即有水平渐近线y=b。
* 先定义函数:
function y=f(x)
syms x; %定义符号变量。
y=exp(-1/2*((x-3)/5)^2)/(sqrt(2*pi)*5);
* 求x趋向无穷大时一阶导数的极限
limit(f,inf)
ans = 0
6)验证 3 sigma 法则
思路:求解概率密度函数在[mu-3*sigma,mu+3*sigma]区间上的积分。
y='exp(-1/2*((x-3)/5)^2)/(sqrt(2*pi)*5)';
double(int(y,-12,18))
ans = 0.9973

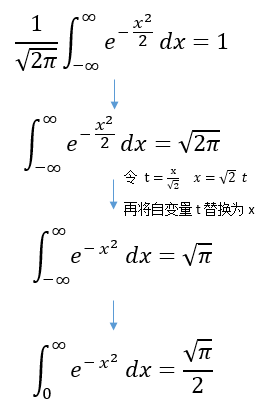







![[基础]-向量点乘和叉乘](https://img-blog.csdnimg.cn/8860a56daa704873b54c8e05ffa8e076.png)