oracle 如何实现excel的正态分布函数normdist
实现目标
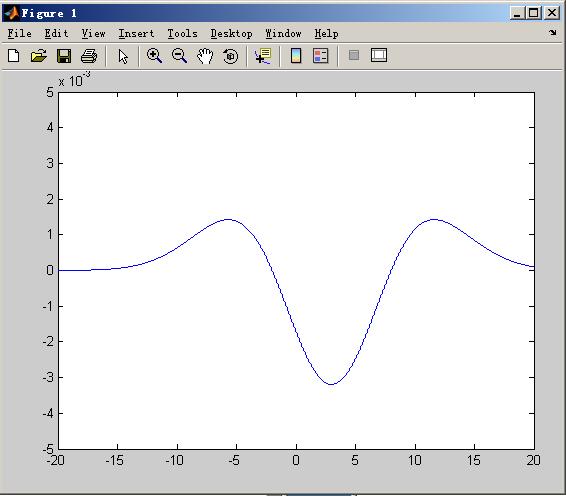
EXCEL中的NORMDIST是指返回指定平均值和标准偏差的正态分布函数。此函数在统计方面应用范围广泛(包括假设检验)。
语法:
NORMDIST(x,mean,standard_dev,cumulative)
X 为需要计算其分布的数值。
Mean 分布的算术平均值。
Standard_dev 分布的标准偏差。
Cumulative 为一逻辑值,指明函数的形式。如果 cumulative 为 TRUE,函数 NORMDIST 返回累积分布函数;如果为 FALSE,返回概率密度函数。
如何在oracle中实现excel的NORMDIST函数?
实现思路分析
1、dbms_random.normal函数是用于生成一组正态分布的随机值。不满足要求;
2、java中可以通过apache-commons-math3.jar包实现正态分布函数计算;
3、oracle是否可通过函数调用Java代码?
java函数调用示例
import org.apache.commons.math3.distribution.NormalDistribution;public class normdist {/*** 计算正态分布值* * <pre>* 方法同excel NORMDIST 函数* </pre>* * @param x* 需要计算其分布的数值* @param mean* 分布的算术平均值* @param standard_dev* 标准偏差* @return 正态分布值*/public static double get(double x, double mean, double standard_dev) {return new NormalDistribution(mean, standard_dev).density(x);}public static void main(String[] args) {for (double d = 0; d < 1.0; d += 0.1) {System.out.println(String.format("%.1f\t %.5f", d, get(d, 0, 4)));}}
}输出:
0.0 0.09974
0.1 0.09970
0.2 0.09961
0.3 0.09946
0.4 0.09924
0.5 0.09896
0.6 0.09862
0.7 0.09822
0.8 0.09776
0.9 0.09724
1.0 0.09667Oacle调用示例
oracle导入jar包
将jar包放到目录下:D:\dev\java_sources\commons-math3-3.0.jar
打开cmd命令窗口,加载jar包:commons-math3-3.0.jar 到oracle中
loadjava -r -f -o -user user/pwd@orcl commons-math3-3.0.jar
创建正态分布函数
-- 创建外部目录,存储jar包
create or replace directory class_dir as 'D:\dev\java_sources';
-- 查看目录
select * from dba_directories;-- 创建java sources
create or replace and compile java source named normdist
as
import org.apache.commons.math3.distribution.NormalDistribution;
public class normdist
{/*** 计算正态分布值* * <pre>* 方法同excel NORMDIST 函数* </pre>* * @param x* 需要计算其分布的数值* @param mean* 分布的算术平均值* @param standard_dev* 标准偏差* @return 正态分布值*/public static double get(double x_in, double mean_in, double standard_dev_in) {return new NormalDistribution(mean_in, standard_dev_in).density(x_in);}
};-- 创建正态分布函数
create or replace function fn_normdist(x_in in number, mean_in in number, standard_dev_in number)
return number
as language java name 'normdist.get(double,double,double)
return double';-- 正态分布函数调用
select fn_normdist(0, 0, 4) as n0, fn_normdist(1, 0, 4) as n1
from dual/*
清理代码
drop function fn_normdist;
drop java source normdist;
*/
调用截图:

参考
https://cloud.tencent.com/developer/ask/149846
https://docs.oracle.com/en/database/oracle/oracle-database/12.2/jjdev/loadjava-tool.html#GUID-AEB08FAD-BE91-45D6-8338-031A70D97C59
https://www.cnblogs.com/mellowsmile/p/4602481.html

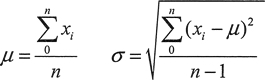








![[基础]-向量点乘和叉乘](https://img-blog.csdnimg.cn/8860a56daa704873b54c8e05ffa8e076.png)