图 1 显示的是正态(或高斯)分布。它是一条连续的贝尔曲线,期望两边的值是相等的,可以理解为期望就是平均值。它是一个概率分布,因此曲线下方的面积是1。正态分布是由两个参数完全定义的:期望和标准差,它们是衡量期望两边的值如何分布的一种方式。
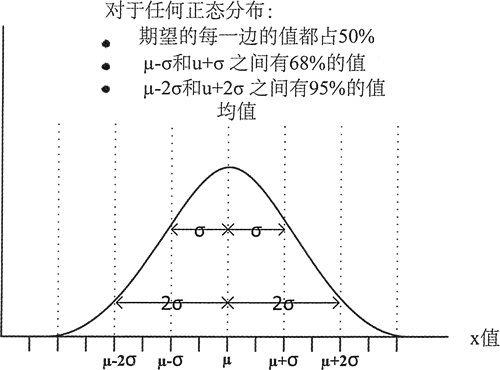
图 1 正态分布
期望和标准差分别是用希腊字母 μ 和 σ 来表示的,变量 x 有 n 个样本,这些是由下面的公式定义的:
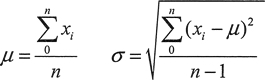
因此,期望就是值的和除以值的个数一换句话说,也就是平均值。可以通过值和期望的差值的平方子和除以 n-1,然后对结果开方来得到标准差。对于不同的期望和标准差的值,正态分布的相对宽度和高度分布曲线的变化是相当大的。但是,分布值总是如图 1 所示。这意味着,如果知道一个符合正态分布的变量的期望和标准差,例如在大量人口中个体的身高,就可以知道 95% 的人身高不超过期望的 2σ。标准正态分布的期望为 0,标准差为 1。
uniform_distribution 模板定义了可以产生随机浮点值的分布对象类型,默认是 double 类型。默认构造函数创建的是标准正态分布,因此期望是 0,方








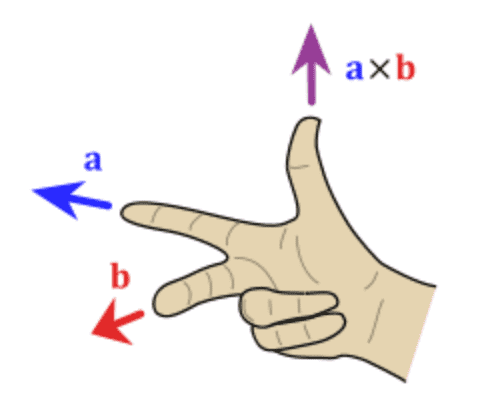
![[基础]-向量点乘和叉乘](https://img-blog.csdnimg.cn/8860a56daa704873b54c8e05ffa8e076.png)