大家好,我是馨馨,一个混过大厂,待过创业公司,有着6年工作经验的软件测试妹纸一枚。近期针对公司项目做了一次完整的安全测试,扫描出来了不少漏洞,价值还挺大的。回顾整个流程,并没有特别复杂的点,小林星球这里程序员还挺多,想着分享下我的实战感悟,希望对做项目的技术人员有所启发。
一、为什么要做安全测试
一)背景概述
随着互联网应用的普及,软件安全性越来越重要了。公司的产品在线上有些小的功能性Bug,可能就是体验性不好,引发用户的一些吐槽,损失一点用户,问题不大,可以不断改进。
但是如果产品有高危漏洞,不小心被黑客袭击,导致服务器瘫痪或资金损失,重要数据泄露和丢失,或者服务器资源被黑客恶意利用,导致公司业务无法正常运转或损失惨重,后果将不堪设想。
二)原因剖析
大家可以稍微留意下,规模稍微大点的公司,一般会有专门的安全测试团队或者请乙方安全公司来进行安全测试。实际上,安全团队也是利用安全扫描工具进行扫描,扫描出来的漏洞大多是常见的SQL注入,跨站点请求伪造CSRF,跨站点脚本攻击XSS等等。
想着工具的学习成本也不高,于是在领导的号召下,在公司内部开启了一轮从0到1的安全测试。
二、安全测试的详细方法
一)测试工具
AppScan,即 AppScan standard edition。其安装在 Windows 操作系统上,可以对网站等 Web 应用进行自动化的应用安全扫描和测试。
简单理解,就是AppScan工具先抓取出所有的接口,接着利用自身的安全用例库,对接口传各种参数,验证接口是否有安全漏洞。
二)测试步骤
基本思路:自动探索--特殊配置--手动探索---仅测试--导出报告。
以测试一个Web应用为例,介绍一次完整的安全测试流程。
1、打开AppScan,文件--新建--扫描Web应用程序

2、填写起始URL地址
这里有个坑:填写登录页面的地址,最好是未登录之前,因为有的页面没有做重定向处理,后续测试的时候会一直提示登录。
比如登录页面的地址是https://XXX/Login,最好别填登录进去后的某个地址例如:https://XXX/Login/index

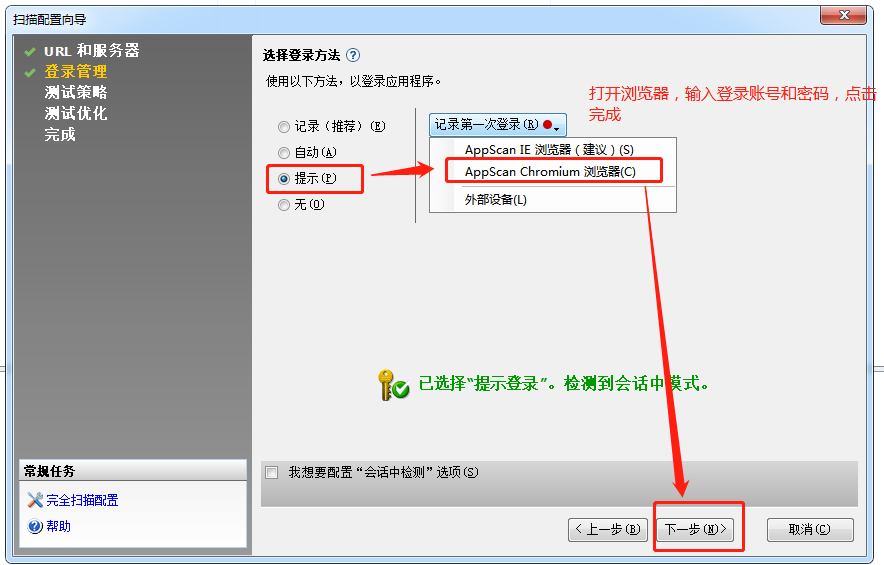
3、填写登录管理信息
登录系统的方式,有三个选项:
1)记录:点击“记录”按钮,进行录制登录操作。操作类似于用LR做脚本录制,适用于没有验证码的场景。
2)自动:输入用户名和密码,扫描时会自动根据这个凭证登录应用程序,推荐没有验证码时,使用该场景。
3)提示:根据扫描地址,每次需要登录时会弹出相应登录页面,如遇后台登录有验证码时推荐使用此场景。
记录和自动的差别不大,都是适用于没有验证码的场景,而且都只需要输入一次用户名和密码,不同之处在于 「记录 」是在浏览器登录页面输入密码,「自动 」是直接在AppScan的页面输入密码。
4、测试策略
在实际测试过程中,要完整的测试就选「完成」策略,一般情况下选「缺省值」策略。
简单介绍下7种测试策略:
1)缺省值:包含多有测试,但不包含侵入式和端口侦听器
2)仅应用程序:包含所有应用程序级别的测试,但不包含侵入式和端口侦听器
3)仅基础结构:包含所有基础结构级别的测试,但不包含侵入式和端口侦听器
4)侵入式:包含所有侵入式测试(可能影响服务器稳定性的测试)
5)完成:包含所有的AppScan测试
6)关键的少数:包含一些成功可能性较高的测试精选,在时间有限时对站点评估可能有用
7)开发者精要:包含一些成功可能性极高的应用程序测试的精选,在时间有限时对站点评估可能有用

5、测试优化
默认即可
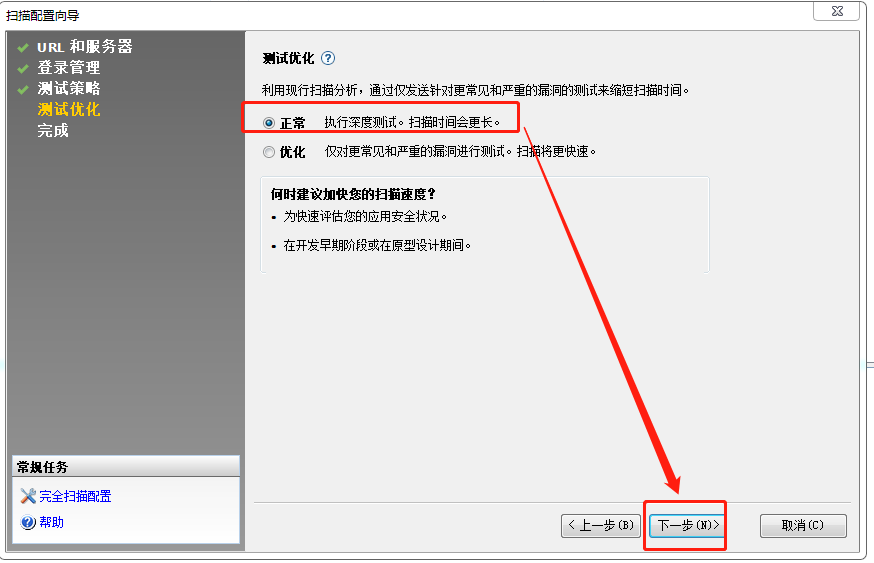
6、完成
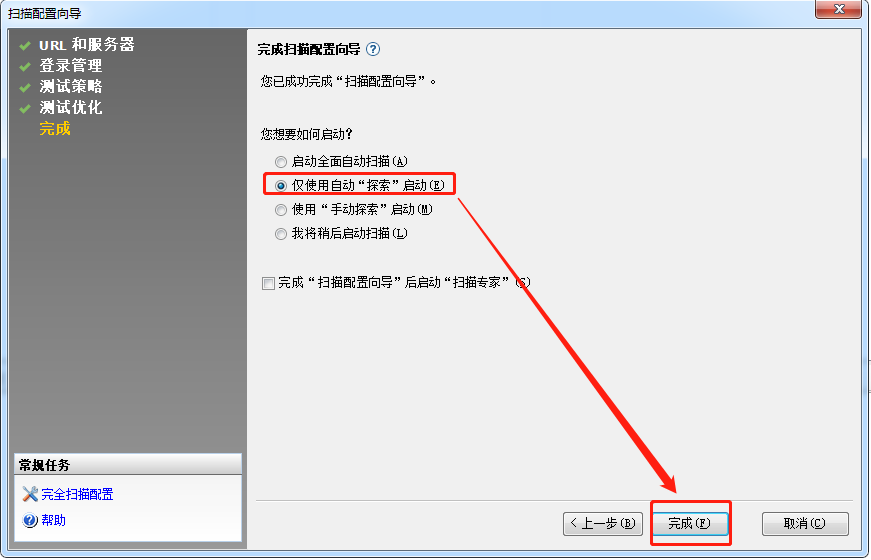
实际测试项目中一般先选择自动“探索”启动,因为还需要设置后面的排除链接,有些接口是不适合做大量测试的,例如一些外部接口,对接的外部项目的线上接口,如果进行测试后,会产生大量的线上脏数据。
有四个选项:
1)启动全面自动扫描:会自动探索URL,而且边探索边扫描页面,也就是边扫描边测试
2)仅使用自动“探索”启动:自动探索URL,不做扫描,只是探索出所有的接口,不对接口进行任何操作
3)使用“手动探索”:手动去访问页面,AppScan会自动记录你访问页面的url
4)我将稍后启动扫描:AppScan不做任何操作,需要自己手动去启动扫描
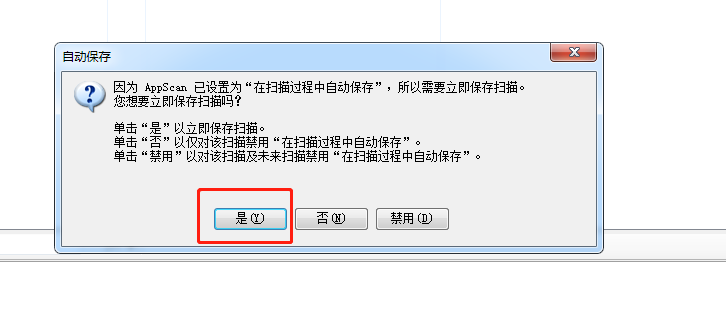
7、保存文件
8、进行第一遍的探索结果

9、操作系统参数设置
根据被测系统,在配置--扫描配置--环境定义,修改操作系统相关参数

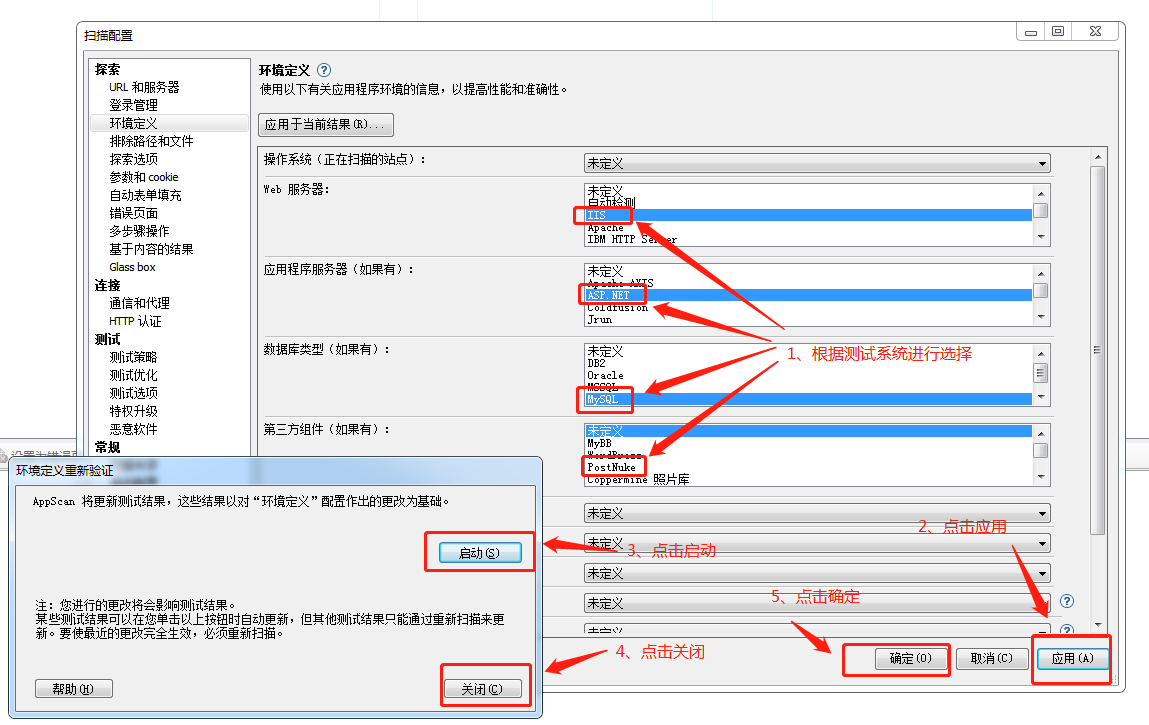
10、屏蔽设置
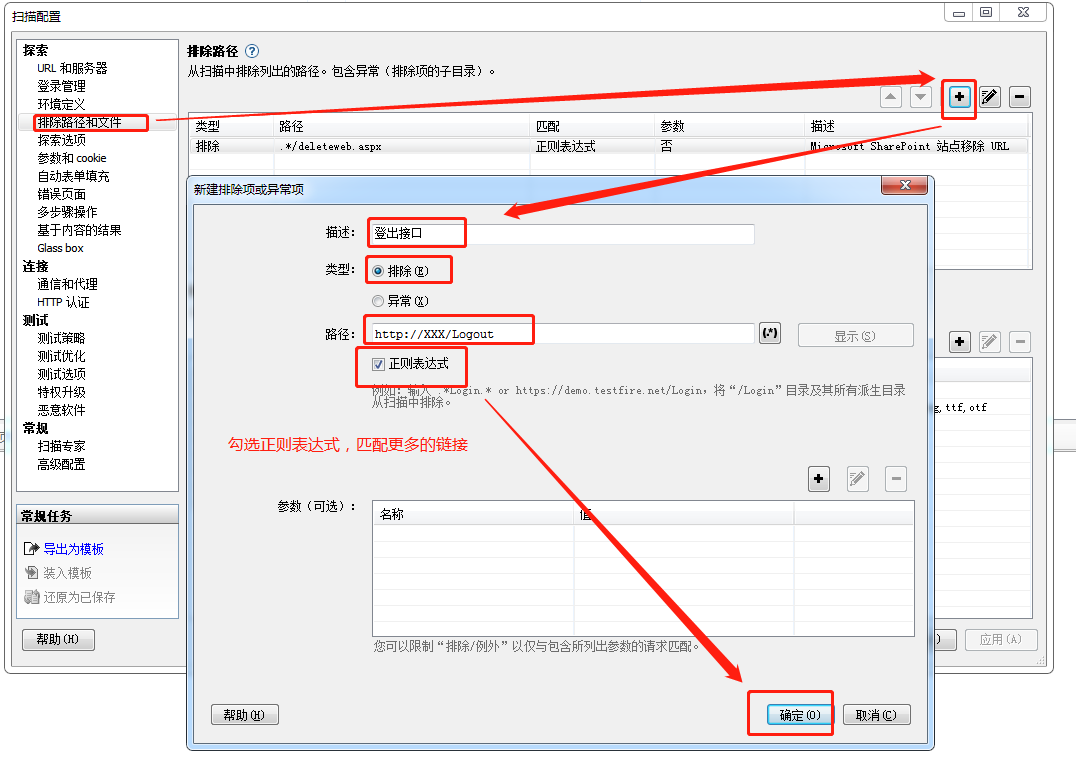
根据被测系统,在配置--扫描配置--环境定义,可排除不需要测试的接口。
在扫描过程中,有些需要排除的接口,例如登出接口,与外部项目对接产生大量生成脏数据的接口等等,可以设置进行排除。
11、线程设置
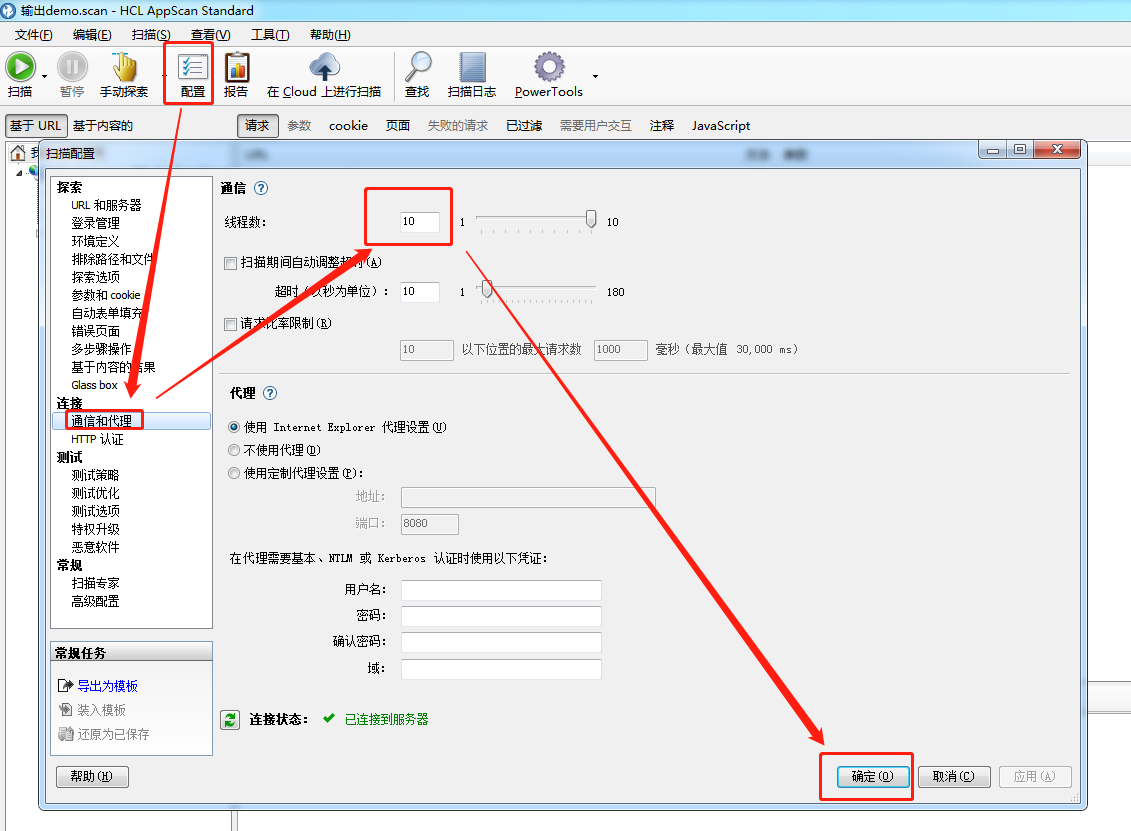
在测试过程中,应用服务出现性能过慢的问题,可在配置--扫描配置--通信和代理中,适当调整线程数为2~5。
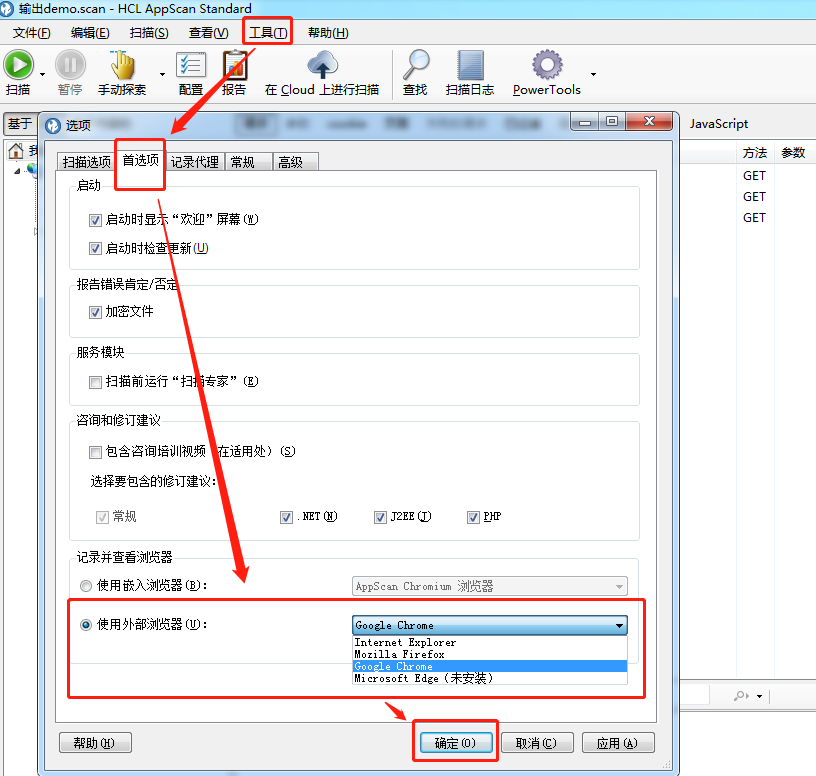
12、浏览器设置
在扫描过程中AppScan自带浏览器如果出现兼容问题,可配置外部服务器,配置如图:
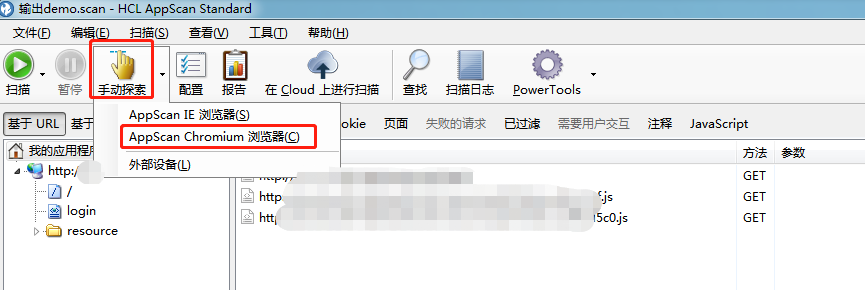
13、进行手动探索
自动探索会出现探索不完整的情况,用手动探索来完善,手动探索,也就是把页面的所有功能都手动点一遍,目的是抓取出所有的接口。
14、添加手动探索出的接口
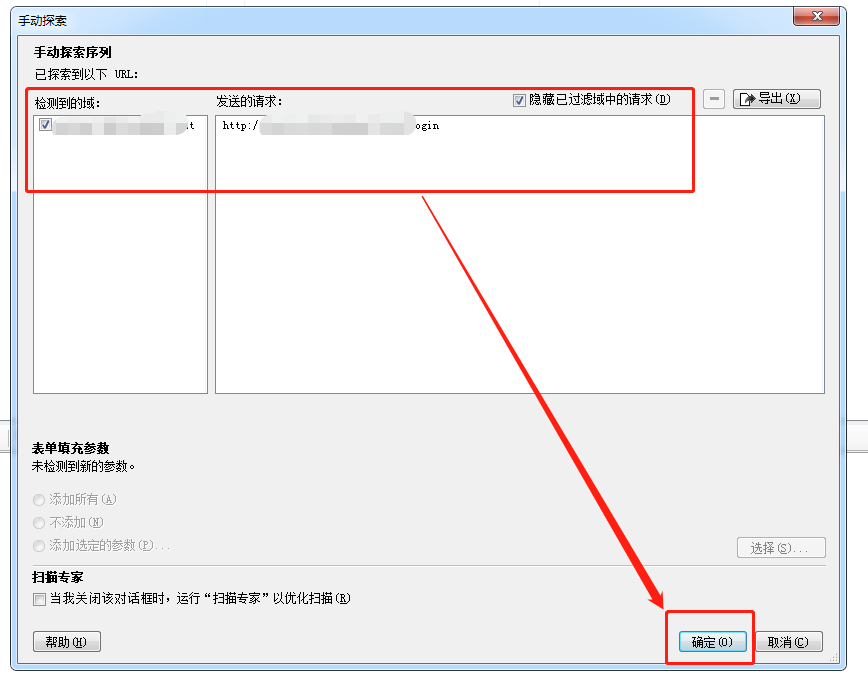
15、进行测试,也就是把刚刚手动探索出的接口,进行测试

16、待扫描完成后,导出报告
注意参数的设置,实际项目中,参数设置如下图所示
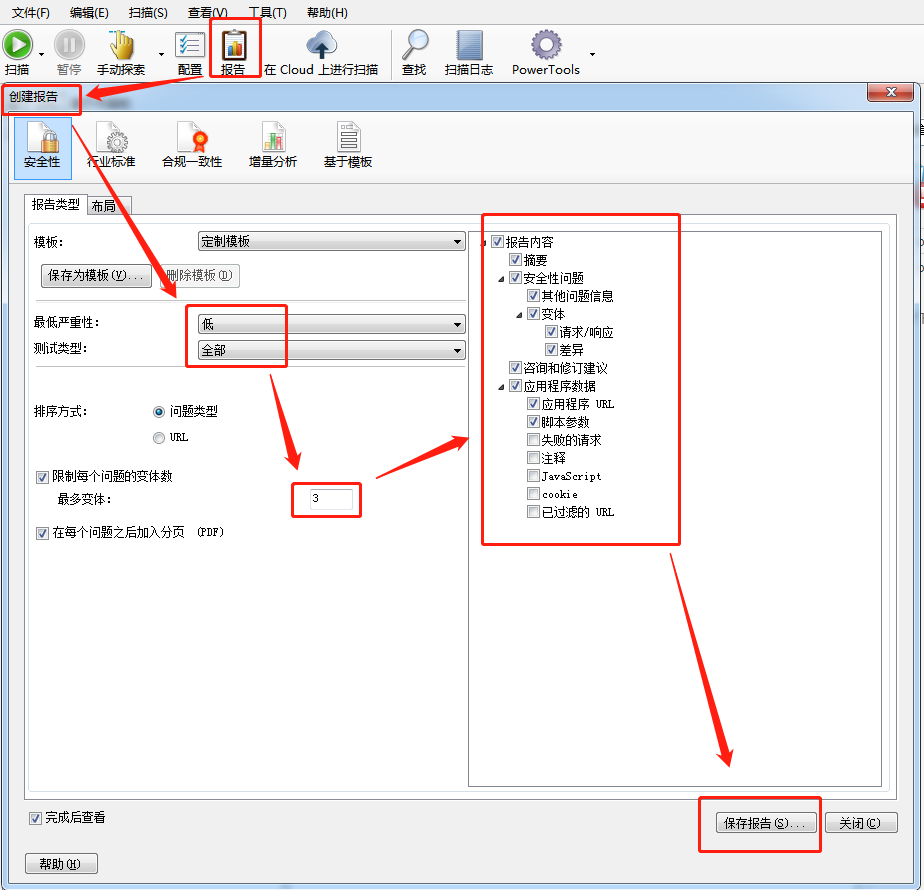
17、二轮测试
在之前scan测试文件的基础上,追加手动探索,扩大扫描范围,然后选择仅测试,就只会测试新扫描出来的接口,最后保存文件,导出报告即可。
三、分析测试结果复现漏洞
报告会显示很多漏洞,等级分为高,中,低,但是有些漏洞是无法重现的,所以需要人工分析,手动复现。
注意:不要轻易点击重新测试,有些问题重新测试之后就没了,这应该是工具问题,实际项目中遇到好多次了,可以先保存一份文件,再复制一份同样的文件出来重新测试。
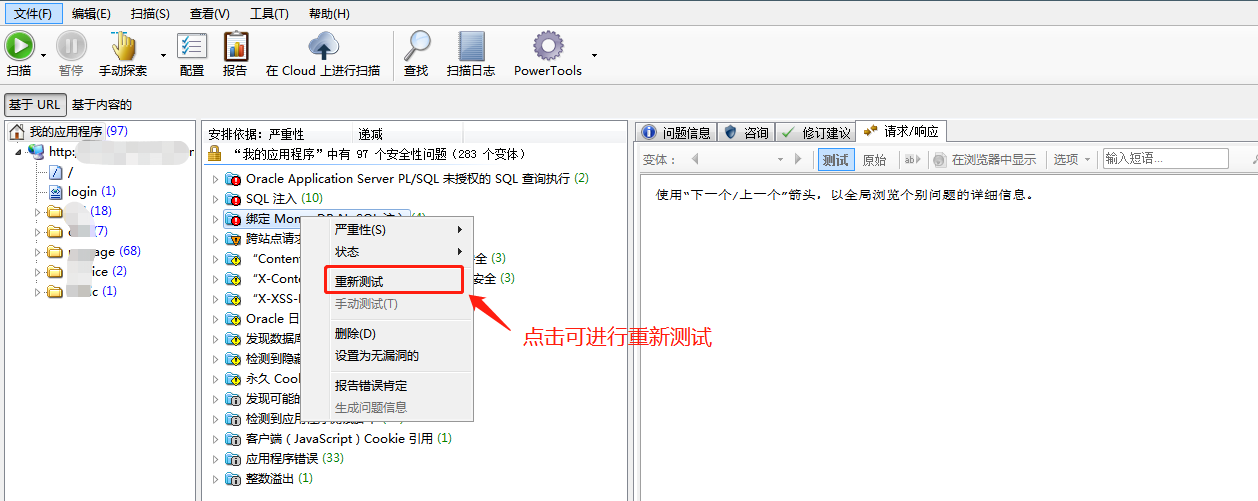
一)常见的漏洞概述
1、SQL注入
1)定义
SQL注入是一种比较常见的高等级漏洞,简单理解,SQL注入就是没有过滤从页面传至接口的字符,攻击者通过将恶意的SQL查询插入到输入参数中,在后台服务器上解析进行执行,最终导致数据库信息被篡改或泄露。
2)风险分析
SQL注入可能导致数据库中存储的用户隐私信息泄露,可通过操作数据库对特定网页进行篡改。修改数据库一些字段的值,嵌入木马链接,进行挂马攻击,甚至数据库的系统管理员帐户被篡改。
3)修复方式
A、程序代码里的所有查询语句,使用标准化的数据库查询语句API接口,设定语句的参数进行过滤一些非法的字符,防止用户输入恶意的字符传入到数据库中执行sql语句
B、对用户提交的的参数安全过滤,像一些特殊的字符(,()*&……%#等等)进行字符转义操作,以及编码的安全转换
2、跨站点请求伪造csrf
1)定义
csrf( Cross-site request forgery):跨站请求伪造,简单说,攻击者盗用了你的身份(借用你的token),以你的名义发送恶意请求,而你却不知情。
恶意攻击者往Web页面里插入恶意的HTML代码,当用户浏览该页之时,嵌入其中Web里面的HTML代码会被执行,从而达到恶意目的。
举个例子:攻击者写了一段删除某个财务系统数据的代码,放在任意一个广告页面的链接上。当其他用户浏览广告页面时,只要有用户例如Emily登录了财务系统,点击了该链接,就会在用户Emily无意识的情况下,以Emily的名义删除了财务系统的很多数据,达到了恶意攻击的目的。
实际的场景:攻击者盗用账号转钱,添加管理员,购买商品,发送邮件等等。
2)风险分析
攻击者可以对系统进行任何增删改查的操作,严重损害了系统的安全性。
3)修复方式
A、添加Token,发请求时带上Token。处理请求的时候需要验证Cookie+Token
B、请求头中Referer参数需要校验请求来源是否是目标网页发出
缺点:
(1)Refer值由浏览器提供,不能保证浏览器自身没有安全漏洞
(2)用户可以自己设置浏览器,让其在发送请求时不提供Refer值
优点:简单易行
实际项目中,一般采用添加Refer请求头和添加Token组合的方式,来防止csrf的攻击。
3、跨站点脚本攻击XSS
1)定义
指利用网站漏洞从用户那里恶意盗取信息。简单理解,就是用户输入中可加入JS等破坏性的代码,而程序没有进行过滤,还执行了这些代码,达到了恶意攻击的目的。
2)分类
主要有存储型、反射型和DOM(基于文档对象模型)三种类型。
存储型:攻击的数据会保存到数据库,一般存在于post的写请求或者get的写请求,例子:例如接口请求参数修改为</script+><script>alert(124)</script>,如果存在漏洞,则会存入数据库,每次页面加载,都会执行一次
反射型:攻击的数据,不存在数据库,属于一次性的,用完一次就没了,一般在get请求参数中构造,与存储型的危害差别不大,例子:例如https://www.XXX.com/test?page=</script+><script>alert(124)</script>,如果存在漏洞,则页面会弹出124的窗口
DOM:没有访问服务端,属于纯前端的行为。例子:直接在前端找到元素,修改为</script+><script>alert(124)</script>之后,如果弹出执行窗口,就证明存在漏洞
三者的区别:
存储型和反射型的区别在于:是否存了数据库;
存储型/反射型与DOM的区别在于:是否访问了服务端。
3)风险分析
可能会窃取或操纵客户会话和 cookie,它们可能用于模仿合法用户,从而使黑客能够以该用户身份查看或变更用户记录以及执行事务。
4)修复方式
使用过滤器,对用户输入执行危险字符清理
4、密码传输未采用复杂加密方式
1)例子
例如密码仅仅采用md5的加密方式,可通过撞库反解密码。
2)风险分析
单向Hash在被截取到传输中的hash值后,攻击者可以伪造一模一样的POST(重放攻击)请求可成功登录。
3)修复方式
A、添加SALT并进行多次Hash的方式对密码进行加密
B、使用更为高级的加密方式进行传输
5、解密的登录请求(不属于漏洞)
1)例子
也就是说在接口请求过程中,例如登录接口,密码参数用的名字为password,工具一般会报出来,非漏洞,业界很多接口都是这么写的。
2)风险分析
只有http接口会存在暴露风险,但是现在大多数都是https接口,无伤大雅。
3)修复方式
使用https请求,确保所有登陆请求都以加密方式发送到服务器。
6、未授权的SQL查询执行
1)定义
对不合法的请求进行了正确的响应,例如去除请求参数,清除HTTP请求体或修改请求方法等等,最后还是返回了状态码200,期望返回除200外的其他状态码。
2)风险分析
没有实质性的危害,主要是规范问题。
3)修复方式
对不合法的请求,不要状态码200,返回其他状态码。
7、恶意站点链接
1)定义
网站中存在恶意站点链接,存在跳转链接,但是要人工自行识别。
2)风险分析
恶意站点可能让用户进入危险页面,导致用户敏感信息泄露。
3)修复方式
对恶意站点或无法访问的站点做下架处理。
8、使用HTTP动词篡改认证旁路
1)风险分析
通过修改HTTP方法后,请求发送成功并且返回的内容“原始响应”的内容完全相同,这表明未对HTTP其他方法(PUT、DELETE)进行限制,导致其他HTTP方法能够绕过站点的认证。
2)修复方式
A、禁用不必要的HTTP方法,一般情况只会保留GET、POST
B、检查tomcat的web.xml,weblogic的weblogic.xml配置,对请求类型进行限制
9、越权
需要手动覆盖。主要分为水平越权和垂直越权。举个例子:
水平越权:在业务系统中,本来用户A只能对自己的个人信息进行增删改查,但是通过抓包,修改用户id(一般用户id都是递增的),可以获取到其他人的个人信息,或者账号A将自己的个人信息页面通过浏览器发送给用户B,用户B登录系统后可以看到用户A的信息,这就是水平越权了。
垂直越权:在业务系统中,本来用户A对某条记录只有查看的权限,但是通过抓包,可以对记录进行修改,这就是垂直越权了。
10、其他
1)支持不推荐使用的SSL版本
只需要开发同学修改配置即可
2)Cookie中无HTTPonly属性
只需要开发同学修改配置即可
二)漏洞复现方式
1、复现SQL注入漏洞
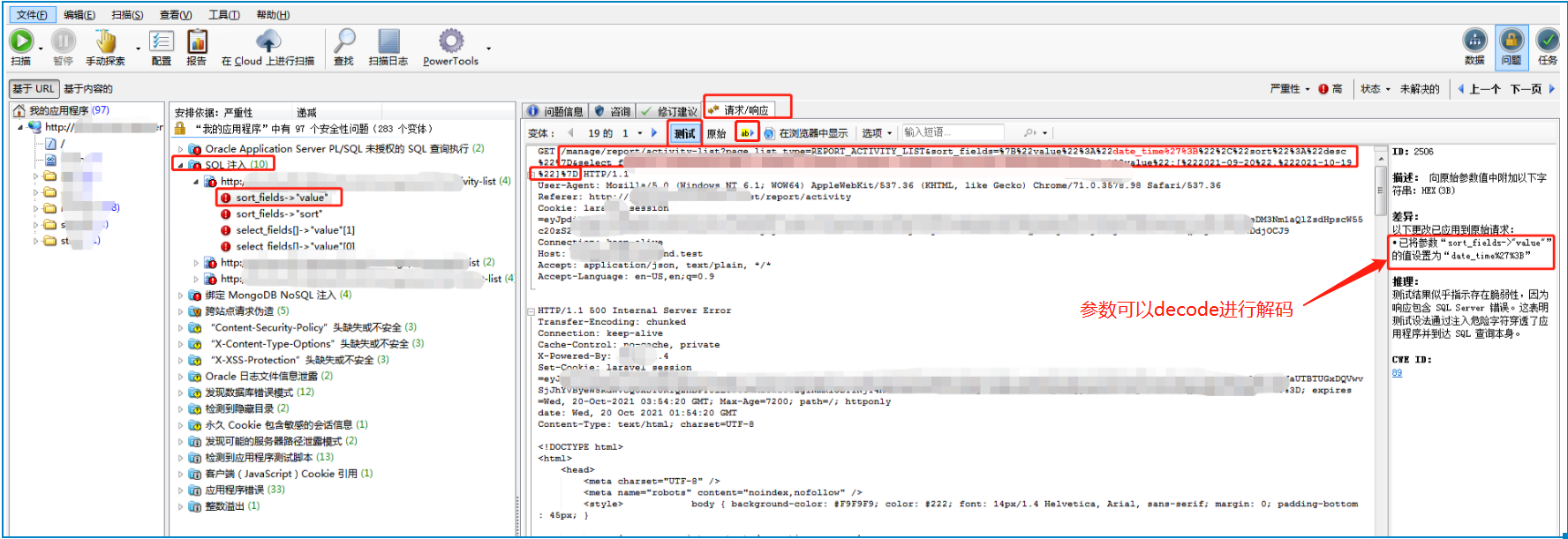
打开扫描的scan文件,选择SQL注入--请求/响应--测试,根据请求信息,进行复现。
分析下这个问题,这个接口主要是将参数sort_fields的值改为date_time%27%3B后,响应信息中出现了数据库的相关信息,说明攻击成功了。(查看数据库相关的报错信息可点击页面的黄颜色ab按钮,一直往下,可查看所有的报错信息)
这是一个get请求,可以直接在浏览器中进行复现,先登录系统,直接在url中输出如图GET后到HTTP/1.1之前的参数,前面加上http://host或https://host,拼接起来就是http://host/manage/report/activity-list?pageXXXXXXXXXXXXXXXsort_fields=%7B%22value%22%3A%22date_time%27%3B%22%2C%22soXXXXXXXXXXXXXXXXXX-20%22,%222021-10-19%22]%7D,即可复现。

2、复现跨站点请求伪造csrf漏洞
在实际的项目中,只要测试报告中有csrf的漏洞问题,就可以人工去查看post或get接口的请求头,是否包含token和referer。

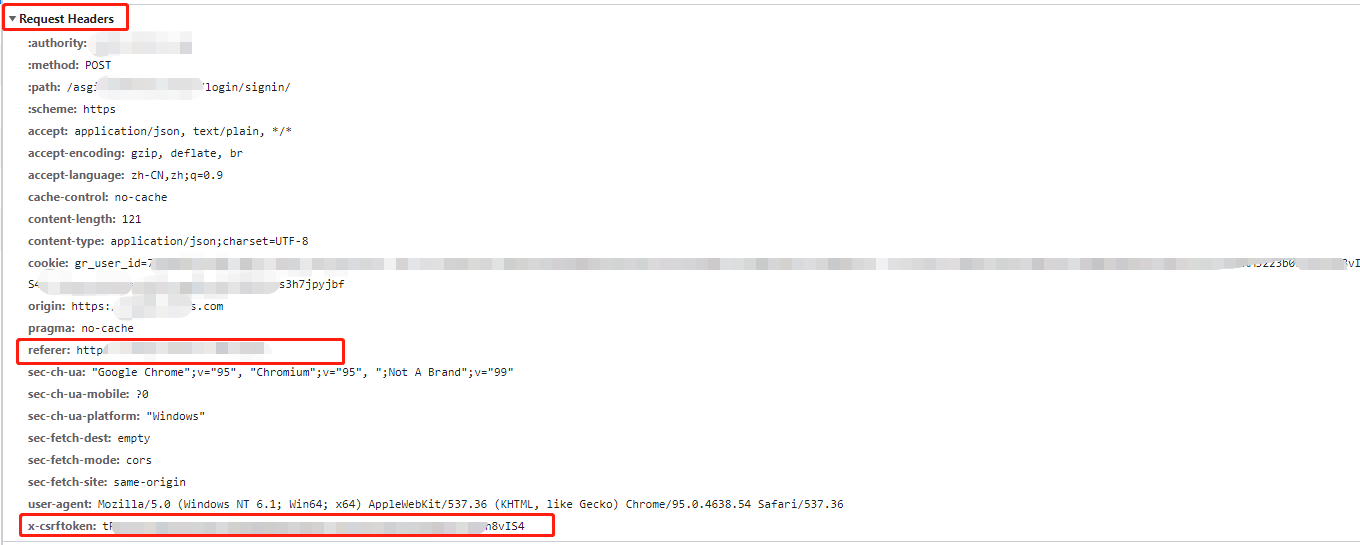
如果没有包含,就去尝试复现,理论上,使用post请求去复现,但是目前团队由于无法解决跨域的原因,还没构造出对应的表单,所以复现就直接用get接口了,当然,如果大家实现了用post去复现的表单,可以慷慨地分享给我哈~
利用get请求复现的方法很简单:
1)在浏览器中登录系统,找到一个get接口链接A,复制下来
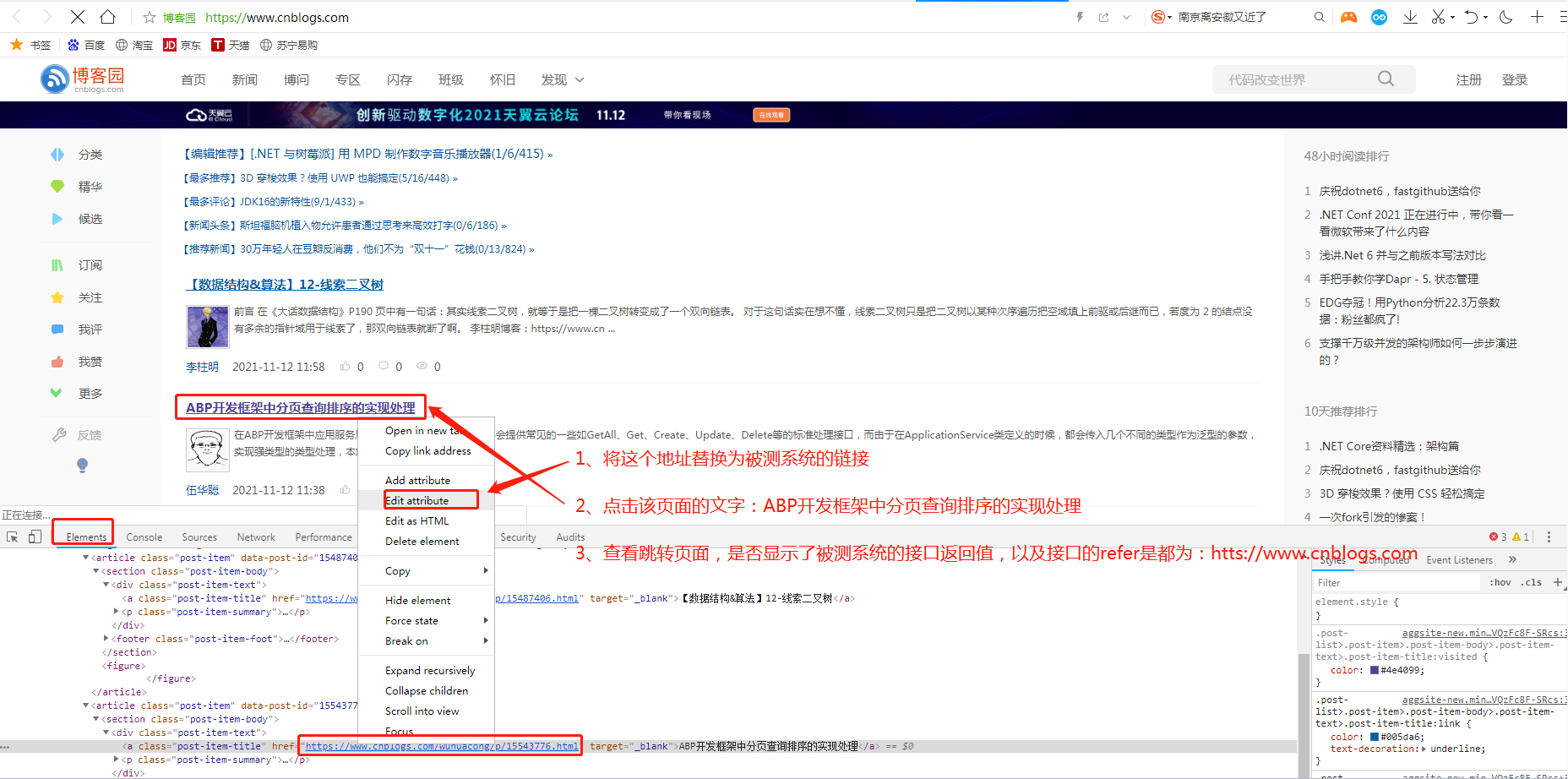
2)再去百度,随便搜索一个博客链接B,找到元素的链接B后,右键,编辑,直接将B替换为所测系统的接口链接A
3)点击博客上刚刚替换链接对应的文字,如果跳转的页面返回了接口A的信息,则证明攻击成功,存在跨站点请求csrf的问题,如果不是,则会返回无权限或接口的其他状态码等等
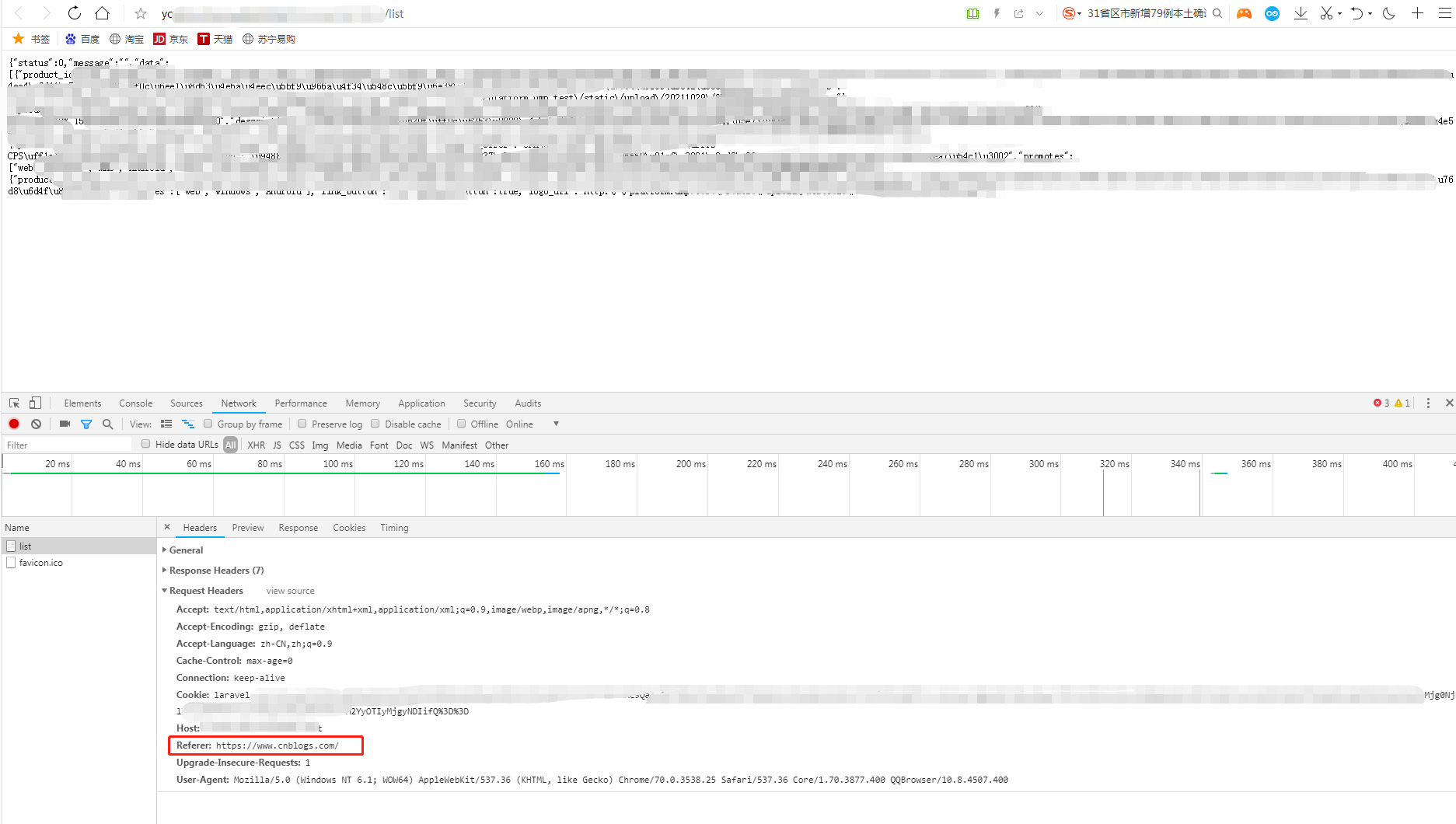
3、复现跨站点脚本攻击XSS漏洞
复现步骤与SQL漏洞复现的步骤几乎一致。
1)打开扫描的scan文件,选择跨站点脚本编制--请求/响应--测试,根据请求信息,进行复现。
分析下这个问题,这个接口主要是将参数skuName的值改为%3C%2Fscript+%3E%3Cscript%3Ealert%28124%29%3C%2Fscript%3E(decode解码后是:</script+><script>alert(124)</script>)后,响应信息中出现了js脚本信息,说明攻击成功了。(查看数据库相关的报错信息可点击页面的黄颜色ab按钮,一直往下,可查看所有的报错信息)
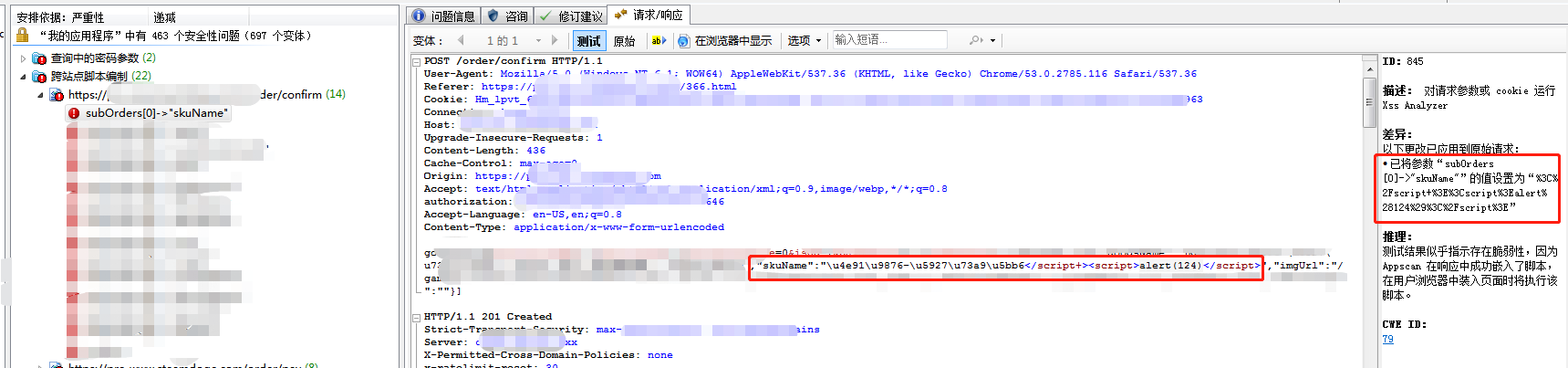

这是一个post请求,可通过接口测试工具例如Jmeter或Postman进行复现,请求参数和请求头信息按照工具上的填写即可。这个XSS漏洞属于存储型的,数据会存到数据库,当攻击成功后,数据会被写入数据库,每次加载页面的时候,都会执行该JS脚本,在页面上可以看到如下的效果。
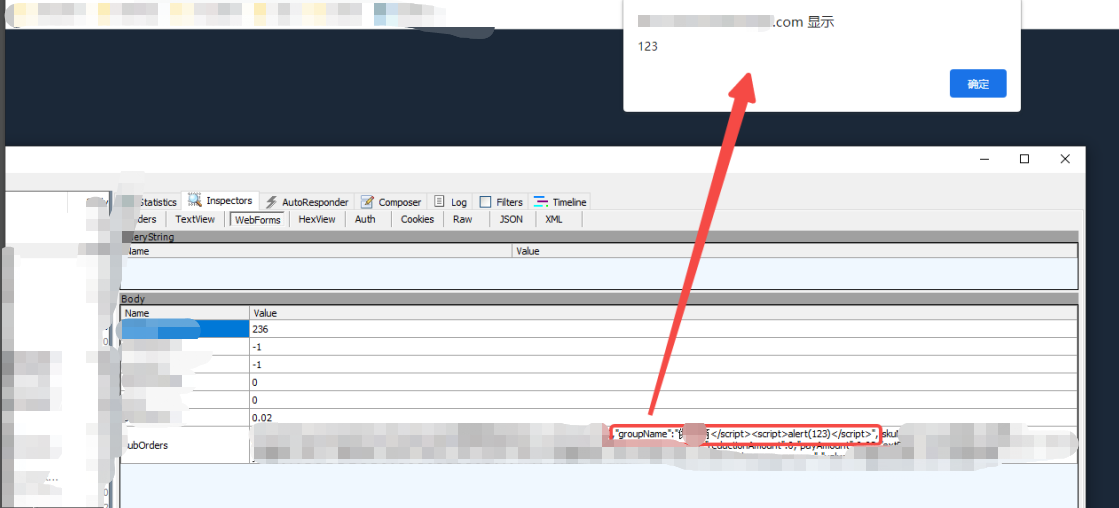
补充:
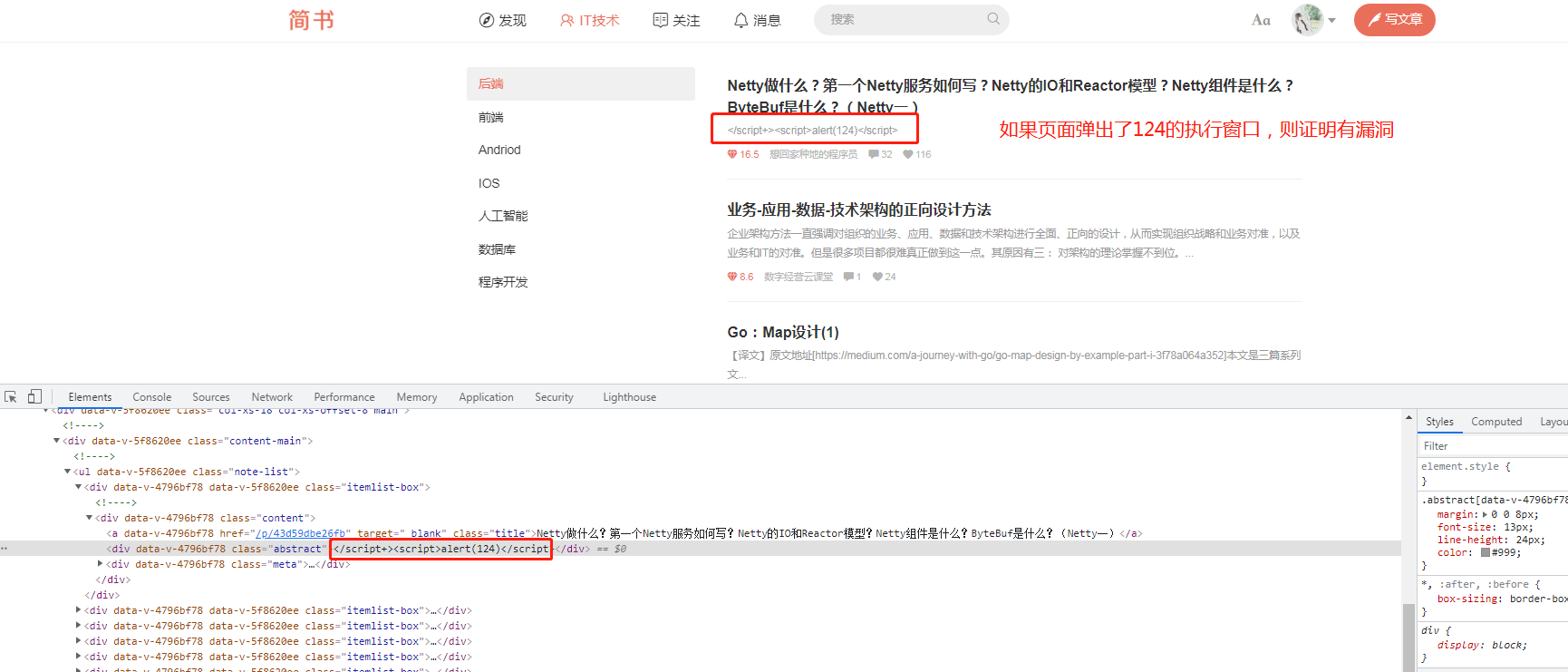
1)复现反射型XSS漏洞的方式,在get接口请求参数中加入</script><script>alert(123456)</script>即可,看页面是否会输出123456,输出了,则证明执行了脚本文件,存在XSS漏洞

2)复现DOM基于文档对象模型漏洞的方式,直接在前端找到元素,修改为</script+><script>alert(124)</script>之后,如果弹出执行窗口,就证明存在漏洞
四、总结测试结果形成报告
一)发送测试报告
以邮件的形式发送测试报告,测试报告主要包含两份附件:导出的安全测试报告和手写的测试报告。
这两份报告的区别:
从生成的scan测试文件直接导出来的报告,会显示所有的问题,高中低都会显示,且有些问题是无法复现的。
而自己手写的测试报告,包含了开发负责人,测试负责人,以及需要修复的漏洞,对比导出的报告,做出了筛选,只列出了需要修复的漏洞,以及对应的接口地址,修复情况等等。
测试邮件则包含:
1、项目名称
2、网址
3、开发负责人
4、测试负责人
5、测试概述(即介绍安全测试的意义)
6、测试范围
7、测试工具
8、风险等级(包含的漏洞风险等级,以及问题总数)
9、风险类型(SQL注入,跨站点请求伪造等等)
10、测试日期
11、安全审计员
具体报告的呈现形式取决于项目组,如果大家对模板感兴趣,可以私聊我领取。
二)开发修复漏洞
待开发同学修复漏洞之后,需要重新验证,验证方法与重现方法一样,可参考重现方法。
验证完后可在之前的scan文件上,用工具验证一轮。
三)回归验证结果
待所有的问题修复完后,回复一个验证报告。
相信大家看完了整个安全测试流程,对安全测试也有了一定的了解,安全测试对于系统的数据和服务器资源等都有着至关重要的作用。今天分享就到这里,希望对大家有所启发。