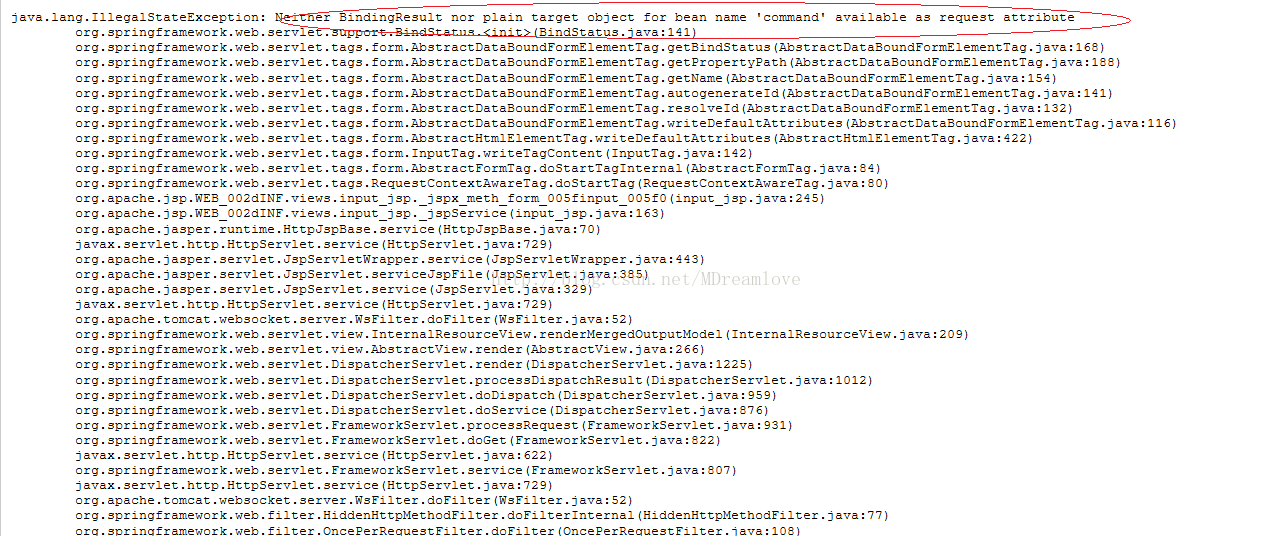
Reason

        这两天学习张贤达的《矩阵分析和应用》，1.3.2节对向量空间的定义扩展，然后突然扩展到线性空间让我很不适应，并不能理解二者的关系。上网一查更迷惑了，很多的线性代数教材倾向于将二者等价，大家对向量空间和线性空间的关系持两种观点：1、向量空间和线性空间二者等价；2、向量空间是线性空间更具体地一种情况或者特例，而线性空间是更抽象化地概念。
        这种情况下，我得作一番查阅资料之后地理解与思考。
        说到线性代数学习也是大一下学期地课程，到现在大四上年代久远不说，私以为学院讲授地线性代数地课程构成十分一般，且不通俗易懂，也不涉及本质。现在，越深入地了解计算机领域，约进入一个特定的计算机方向，会发现线性代数地理论在日后研究中发挥的作用。所以现在更愿意不那么功利地去好好学习一下矩阵论，打下一部分基础吧。

Result

        这里还是先写出我目前对向量空间和线性空间关系的理解，仅限与目前。
        首先线性空间是更抽象的概念，它满足非空集合V，在数域上K上定义的加法和标量乘法运算，同时还满足四条加法（交换、结合、零元素、负元素）和四条乘法（结合、两个标量分配、单位）法则。而，向量空间中向量只是满足上述要求的线性空间的具体化，当我们对于其他的集合和数域可以定义加法和标量乘法运算，且满足八条运算性质时，都可以作为线性空间的一种表示，譬如可能矩阵空间、函数空间等。

Process

        先看一下我问题地出处，张贤达的《矩阵分析和应用》1.3.2节。截止到目前这本书还是十分适合工科生作为应用矩阵论的学习材料，不拘泥于定理证明，并结合领域应用实例。
        这里前面说以向量为元素的集合V称为向量空间，后面直接没有停顿的句号，把两个闭合性：加法和标量乘法、加法四公理、乘法四公理满足之后就跳到了服从加法四律和乘法四律的向量空间为线性空间。我一脸问号，？？？？，教材截至到此没指出线性空间就是满足加法和标量乘法、加法四公理、乘法四公理的啊。

pic1：张贤达的《矩阵分析和应用》1.3.2节 P17-18

        于是去百度，发现知乎这个问题下面有不少讨论。

问题传送门 不少答主认为向量空间和线性空间二者等价，并且说不少通用教材上也是没有明确区分，我翻看评论区，还是有不少答主的真知灼见和我潜在意识相合，譬如：

pic2：截图

        之后就翻阅手头上的几份线代教材，看看他们的定义，包括《工程数学 线性代数》统计大学第五版 同济大学数学系，《简明线性代数》 丘维声，《线性代数讲义》袁海荣。

         这里因为并将没有对每本书全书进行大概了解，只是通过目录查找和向量空间和线性空间定义相关的章节来进行考察。

         展示一下截图：

pic3《工程数学 线性代数》统计大学第五版 同济大学数学系 P102-103

pic4《工程数学 线性代数》统计大学第五版 同济大学数学系 P138-139

        这里在前面，对向量空间进行定义之后，第六章进行向量空间与线性空间等同，并进行抽象扩展。

pic5：《简明线性代数》 丘维声 P217-219

        这里对线性空间进行抽象化描述，即满足集合在数域上加法和标乘两个运算，四加、四乘四条法则，又说明几何状态下，线性空间可称为集合空间。私以为，按照由n维向量张成的向量空间不是直观意义上的集合，但是这里向量空间是线性空间在一定情况下的特例已经比较明显了。

pic5：《线性代数讲义》袁海荣 P86-88

        而这里袁老师的讲义中，对后面明确指出，线性空间的元素可以是向量，也可以是其他的类型，必须的是满足集合和数域上定义的加法和标乘运算，再加八条运算性质。

Others

        查资料的过程中，发现一篇blog写的很不错 点击查看，也下载了博主推荐的齐民友老师的《重温微积分》，什么时候也可以对数学有更加深刻、体系的认识。