向量空间的概念

定义：设 V 是 n 维向量的集合，如果满足

1. 若 a ∈ V， b ∈ V，则a + b ∈ V ．（对加法封闭）
2. 若 a ∈ V，k∈ R，则ka ∈ V ． （对数乘封闭） 那么就称集合 V 为向量空间．

注： 向量空间就是对加法和数乘两种运算封闭的向量组.
定义：如果向量空间 V 的非空子集合 V1对于 V 中所定义的 加法及数乘两种运算封闭，则称 V1是 V 的子空间．

几个常见的向量空间

1. n 维向量的全体Rn
   R n = { x = ( x 1 , x 2 , . . . , x n ) T ∣ x 1 , x 2 , . . . , x n ∈ R } R^{n}=\{x=(x_{1},x_{2},...,x_{n})^{T}|x_{1},x_{2},...,x_{n} \in R\} Rn={x=(x1​,x2​,...,xn​)T∣x1​,x2​,...,xn​∈R}
2. 齐次线性方程组的解集 S = { x ∣ A x = 0 } S = \{ x | Ax = 0 \} S={x∣Ax=0}称为齐次 线性方程组的解空间.
3. 向量组的生成空间
   

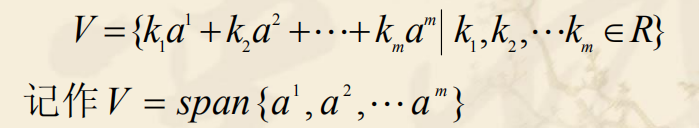
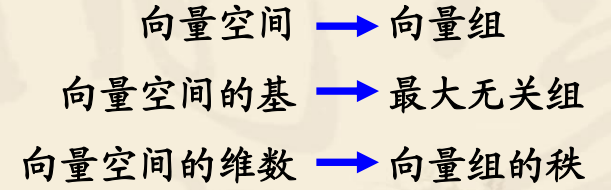
向量空间和向量组的对应关系

内积的概念

设向量$a=\left(\begin{array}{c}{a}_1\\ a_2\\ ...\\ a_n\end{array}\right)$，$b=\left(\begin{array}{c}{b}_1\\ b_2\\ ...\\ b_n\end{array}\right)$，称数
$(a,b)=a_1{b}_1+a_2{b}_2+...+a_n{b}_n=a^{T}b=b^{T}a$为向量的内积。
注：内积就是数量积的推广。
内积具有下列性质（k 为实数）：

• 对称性：$(x,y)=(y,x)$
• 线性性：$(kx,y)=k(x,y)$,$(x+y,z)=(x,z)+(y,z)$
• 非负性：当 x = 0（零向量） 时，$(x,x)=0$;当 x ≠ 0（零向量） 时，$(x,x)>0$。

向量的长度和夹角

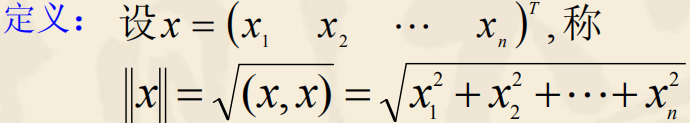
为n维向量的长度（模，范数）。长度为1的向 量称为单位向量。‘
向量的单位化$\frac{x}{||x\Vert |}$
定义：非零向量x,y的夹角定义为$\theta =arccos\frac{(x,y)}{||x||\ast ||y||}$

向量的正交

定义：若向量a,b的夹角为 $\frac{\pi }{2}$ ,称向量a,b正交,记为$a\perp b$. 规定零向量与任何向量正交.
定理：两个n维向量正交的充要条件是它们的内积等于零.
例如：单位坐标向量两两正交.
定理：两两正交的非零向量一定线性无关，反之不对.
定义 如果向量空间V的一组基两两正交且长度 都为1，则称为一组规范正交基.
例如R3的一组规范正交基为:$\left(\begin{array}{c}1\\ 0\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 0\\ 1\end{array}\right)$

正交矩阵

若n阶方阵A满足$A^{T}A=I$,则称A为正交矩阵.
定理 A为正交矩阵的充要条件是A的列（行）向量 是两两正交的单位向量，即为Rn的一组规范正交基.
正交矩阵的性质
若A为正交矩阵则有：$A^{-1}=A^T,|A|=\pm 1$
如果A, B是正交矩阵,则A-1, AT, AB也是正交矩阵.