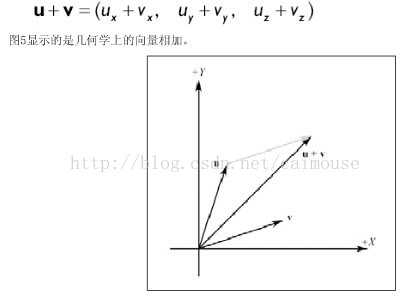
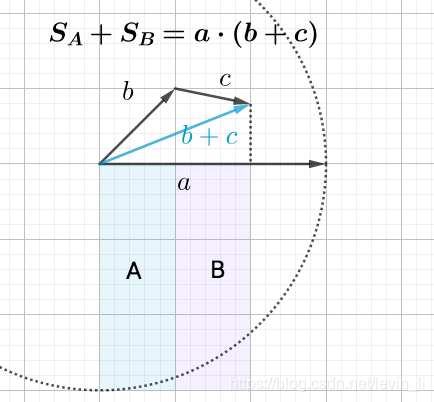
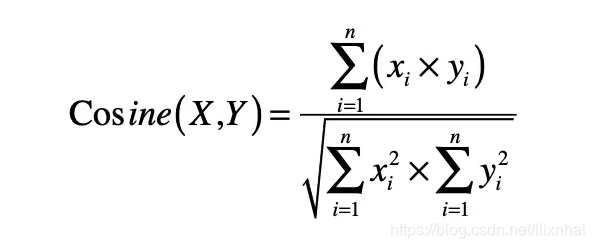向量 AB(AB上面有→)的大小(或长度)叫做向量的模,记作|AB|(AB上有→)或|a|(a上有→)。
向量空间又称线性空间,是线性代数的中心内容和基本概念之一。在解析几何里引入向量概念后,使许多问题的处理变得更为简洁和清晰,在此基础上的进一步抽象化,形成了与域相联系的向量空间概念。譬如,实系数多项式的集合在定义适当的运算后构成向量空间,在代数上处理是方便的。单变元实函数的集合在定义适当的运算后,也构成向量空间,研究此类函数向量空间的数学分支称为泛函分析。 向量空间它的理论和方法在科学技术的各个领域都有广泛的应用。
定义(向量空间)一个 向量空间 是由一些被称为向量的对象构成的非空集合V,在这个集合上定义两个运算,称为加法和标量乘法(标量取实数),服从以下公理(或法则),这些公理必须对V中所有向量u,v,w及所有标量c和d均成立。总的来说就是一个集合,有2种运算,满足8条运算律,这样的代数系统就是向量空间.线性变换就是一种映射,V映射到V自身的映射,且保持2种运算
u,v之和表示为u+v,仍在V中
u+v=v+u
(u+v)+w=u+(v+w)
V中存在一个零向量0,使得u+0=u
对V中每个向量u,存在V中向量-u,使得u+(-u)=0
u与标量c的标量乘法记为cu,仍在V中
c(u+v)=cu+cv
(c+d)u=cu+du
c(du)=(cd)u
1u=u
公理4中的 零向量 是惟一的。对V中每个向量u,公理5中向量-u称为u的 负向量 。
定义(子空间)向量空间V的一个 子空间(subspace) 是V的一个满足以下三个性质的子集H:
V中的零向量在H中
H对向量加法封闭,即对H中任意向量u,v,和u+v仍在H中
H对标量乘法封闭,即对H中任意向量u和任意标量c,向量cu仍在H中
向量空间V中仅由零向量组成的集合是V的一个子空间,称为 零子空间 ,写成{0}。
定理1(集合生成的子空间) 若
在向量空间V中,则Span{}是V的一个子空间。我们称Span{}是由{}生成(或张成)的 子空间 ,任给V的子空间H,H的生成(或张成)集是集合{} ⊂ H,使得H=Span{
向量空间的这个定义概括了平面的基本几何特性。因此,一个平面可以转换成一个向量空间,而此时的向量集合就是平面上点的集合。显然,在实数域的三维欧氏空间中,向量加法和纯标量的乘法的定义也是相同的。
1. C++标准模板库从入门到精通
2.跟老菜鸟学C++
向量空间又称线性空间,是线性代数的中心内容和基本概念之一。在解析几何里引入向量概念后,使许多问题的处理变得更为简洁和清晰,在此基础上的进一步抽象化,形成了与域相联系的向量空间概念。譬如,实系数多项式的集合在定义适当的运算后构成向量空间,在代数上处理是方便的。单变元实函数的集合在定义适当的运算后,也构成向量空间,研究此类函数向量空间的数学分支称为泛函分析。 向量空间它的理论和方法在科学技术的各个领域都有广泛的应用。
定义(向量空间)一个 向量空间 是由一些被称为向量的对象构成的非空集合V,在这个集合上定义两个运算,称为加法和标量乘法(标量取实数),服从以下公理(或法则),这些公理必须对V中所有向量u,v,w及所有标量c和d均成立。总的来说就是一个集合,有2种运算,满足8条运算律,这样的代数系统就是向量空间.线性变换就是一种映射,V映射到V自身的映射,且保持2种运算
u,v之和表示为u+v,仍在V中
u+v=v+u
(u+v)+w=u+(v+w)
V中存在一个零向量0,使得u+0=u
对V中每个向量u,存在V中向量-u,使得u+(-u)=0
u与标量c的标量乘法记为cu,仍在V中
c(u+v)=cu+cv
(c+d)u=cu+du
c(du)=(cd)u
1u=u
公理4中的 零向量 是惟一的。对V中每个向量u,公理5中向量-u称为u的 负向量 。
定义(子空间)向量空间V的一个 子空间(subspace) 是V的一个满足以下三个性质的子集H:
V中的零向量在H中
H对向量加法封闭,即对H中任意向量u,v,和u+v仍在H中
H对标量乘法封闭,即对H中任意向量u和任意标量c,向量cu仍在H中
向量空间V中仅由零向量组成的集合是V的一个子空间,称为 零子空间 ,写成{0}。
定理1(集合生成的子空间) 若
在向量空间V中,则Span{}是V的一个子空间。我们称Span{}是由{}生成(或张成)的 子空间 ,任给V的子空间H,H的生成(或张成)集是集合{} ⊂ H,使得H=Span{
}。
向量空间的这个定义概括了平面的基本几何特性。因此,一个平面可以转换成一个向量空间,而此时的向量集合就是平面上点的集合。显然,在实数域的三维欧氏空间中,向量加法和纯标量的乘法的定义也是相同的。
1. C++标准模板库从入门到精通
http://edu.csdn.net/course/detail/3324
2.跟老菜鸟学C++
http://edu.csdn.net/course/detail/2901
3. 跟老菜鸟学python
http://edu.csdn.net/course/detail/2592
4. 在VC2015里学会使用tinyxml库
http://edu.csdn.net/course/detail/2590
5. 在Windows下SVN的版本管理与实战
http://edu.csdn.net/course/detail/2579
6.Visual Studio 2015开发C++程序的基本使用
http://edu.csdn.net/course/detail/2570
http://edu.csdn.net/course/detail/2582
http://edu.csdn.net/course/detail/2672