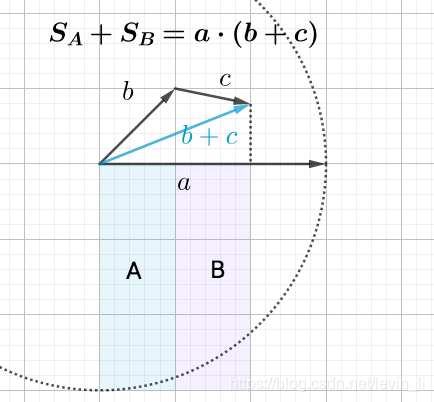
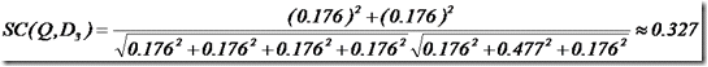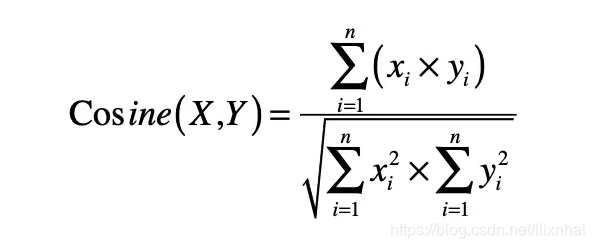进入了向量空间才算开始了线性代数的大门。几个重要的概念：

• 列空间包含所有列向量的线性组合，记作$C(A)$；
• 当且仅当$b$在$A$的列空间时，$AX=b$才有解；

一个$m\times n$的系数矩阵$A$的列空间有可能属于和向量分量一样多的空间$R^m$，也有可能只是子空间。

一、转置矩阵Permutation

转置矩阵适用于执行行交换的。回忆一下我们上一节讲到的$A=LU$分解，一个矩阵$LU$的$L$的特征非常明显，它是进行的行变换的直观矩阵：
$$A=LU=\left[\begin{array}{cccc}1& 0& 0& 0\\ X& 1& 0& 0\\ X& X& 1& 0\\ X& X& X& 1\end{array}\right]\left[\begin{array}{cccc}1& X& X& X\\ 0& 1& X& X\\ 0& 0& 1& X\\ 0& 0& 0& 1\end{array}\right]$$如果考虑行交换，那么一个可逆矩阵的$A$更广泛的消元过程应该表示为：$PA=LU$，Permutation矩阵的性质：

• $P$一定可逆的
• 逆等于转置

性质1，因为转置矩阵就是单位矩阵通过不同组合的行交换组成的，当然也可以乘以一个相反的行交换换回单位矩阵。性质2，举个直观的例子，假设一个转置矩阵

$$P=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]P^T=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 1& 0& 0\\ 0& 0& 0& 1\end{array}\right]$$它是一个单位矩阵第二和第三行的交换。$P{P}^T=I$必然成立！

转置矩阵的数学表达：
$$(A^T{)}_{ij}=A_{ji}$$
对称矩阵(Symmetrix)的定义：
$$A^T=A$$数字是最直观的，一个对称阵$A$应该是：
$$A=\left[\begin{array}{ccc}3& 1& 7\\ 1& 2& 9\\ 7& 9& 4\end{array}\right]$$一个对称矩阵具有转置不变性。我们可以如何获取一个转置矩阵？答案是$R{R}^T$!矩阵总是可以乘以其转置，举个例子：
$$\left[\begin{array}{cc}1& 3\\ 2& 3\\ 4& 1\end{array}\right]\left[\begin{array}{ccc}1& 2& 4\\ 3& 3& 1\end{array}\right]=\left[\begin{array}{ccc}10& 11& 7\\ 11& 13& 11\\ 7& 11& 17\end{array}\right]$$这个是显然的，因为$(R{R}^T{)}^T=(R^T{)}^T{R}^T=R{R}^T$。转置等于其本身，符合转置矩阵的定义。

二、向量空间和子空间

定义：$R^n$空间是所有$n$个分量列向量的组合。$R^5$表示的是五个分量的列向量集合，如
$$\left[\begin{array}{c}3\\ 4\\ 8\\ 1\\ 6\end{array}\right]\left[\begin{array}{c}3\\ 4\\ -1\\ 3\\ 2\end{array}\right]$$
如果你能枚举所有的这样的向量，那么这个集合组成的就是$R^n$空间。或者你也可以这么理解，空间的一个点所能表达的最小坐标数。

2.1 向量空间

向量空间是向量集合，在向量集合满足一定规则的向量称为子空间。

子空间是一系列满足一定运算规则构成的所有向量集，这个规则是满足以下条件，

• 任取向量空间中的两个向量$v$和$w$，$v+w$仍然在这个空间;
• 任取一个标量$c$，$cv$属于这个空间；

换句话说，所有向量线性组合都是在子空间。

$R^2$就是一个空间向量，其向量集合是所有二维实向量，对于其中的如：
$$\left[\begin{array}{c}3\\ 2\end{array}\right]\left[\begin{array}{c}0\\ 0\end{array}\right]\left[\begin{array}{c}\pi \\ e\end{array}\right]$$无论我们这些二维实向量做何线性运算，其结果仍然在空间$R^2$内。

$R^2$空间就是平面空间，随意选取平面上向量集合，如截取$R^2$平面一部分：第一象限，这个平面是否是空间向量呢？不是的，画个图看看：

$w=u-v$显然已经不在指定的第一象限，不符合向量空间的定义。

2.2 子空间

前面在$R^2$空间划取第一象限不是一个向量空间。那么在一个向量空间中任意划取一部分，是否有可能组成一个向量空间？答案是肯定的！！如一个过原点的直线空间！

我们随便在蓝色的空间任意选取一个点组成向量，无论我们如何线性组合它仍然属于这个蓝色区域，符合向量空间的定义！能够再举一个例子吗？当然可以，如零向量空间，不过逆只能取到一个向量，零向量的线性组合仍然是零向量。ok！至此，我们找到了$R^2$所有的三种子空间（线面）都被我们找到了！

对于$R^3$也是一个向量空间，三个实数构成一个向量，向量间的线性运算并不会离开$R^3$空间，如：
$$\left[\begin{array}{c}3\\ 2\\ 1\end{array}\right]\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]\left[\begin{array}{c}\pi \\ e\\ 4\end{array}\right]$$
同样的我们也对$R^3$的子空间，进行查找。第一个，过原点的平面：

在这个平面上任取向量进行线性组合，其结果仍然再这个平面上，是一个子空间。
过原点的直线：

显然，同理，它是一个子空间。最后，原点，也是一个子空间。

为什么$R^2$ $R^3$的子空间都包含零向量？对于更高维度的子空间是否也包含零向量？原因很简单，如果你是一个向量空间，任取一个向量$v$，对于任意实数必须有：$kv$成立，如果我们取$k=0$，他就是一个零向量！这也说明，如果一个空间连零向量都没有那他一定不是向量空间。

2.3 矩阵的列空间

矩阵的列向量的所有的线性组合必然在某个向量空间中，我们将列向量的线性组合的所有可能称为矩阵的列空间。举个例子:
$$\left[\begin{array}{cc}1& 3\\ 2& 3\\ 4& 1\end{array}\right]$$这个矩阵构成的
矩阵的列空间是一个过原点的$R^3$子空间：平面。当然如果列向量是一个共线向量，那么子空间则是过原点的$R^3$子空间：直线。我们矩阵列构成的空间称为矩阵到列空间，记作$C(A)$。

2.4 向量空间具体的定义

设$V$是一个非空集合，$\mathbb{R}$为实数域。如果在$V$中定义了一个加法，即对于任意两个元素$\alpha ,\beta \in V$，总有唯一的一个元素$\gamma \in V$与之对应，称为$\alpha$与$\beta$的和，记为$\gamma =\alpha +\beta$；在$V$中又定义了一个数与元素的乘法（简称数乘），即对于任一数$\lambda \in \mathbb{R}$与任一元素$\alpha \in V$，总有唯一的一个元素$\delta \in V$与之对应，称为$\lambda$与$\alpha$的数量乘积，记作：$\delta =\lambda \alpha$，并且这两中运算满足以下八大运算规律（设$\alpha$、$\beta$、$\gamma$ $\in$$V$，$\lambda$ 、$\mu$ $\in$ $\mathbb{R}$）：

• $\alpha +\beta =\beta +\alpha$
• $(\alpha +\beta )+\gamma =\alpha +(\beta +\gamma )$
• 在$V$中存在零元素$0$，对任何$\alpha \in V$，都有$\alpha +0=\alpha$

！！！向量空间必须包含零空间