实数域定义向量

设有一个数的集合 F，它满足“F 中任意两个数的加减乘除法（除数不为零）的结果仍然在这个 F 中”，我们就可以称 F 为一个“域”。我们处理的数据通常都是实数，所以这里我只考虑实数域。而如果域 F 里的元素都为实数，那么 F 就是实数域。

如果 x1​，x2​，……，xn​∈F，那么 F 上的 n 维向量就是，

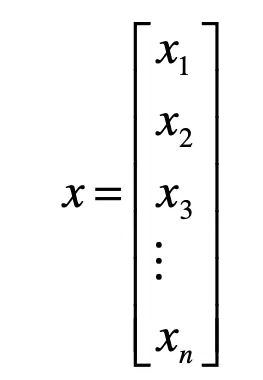
向量中第 i 个元素，也称为第 i 个分量。Fn​ 是由 F 上所有 n 维向量构成的集合。

向量中第 i 个元素，也称为第 i 个分量。Fn​ 是由 F 上所有 n 维向量构成的集合。

向量空间

假设 V 是 Fn​ 的非零子集，如果对任意的向量 x、向量 y∈V，都有 (x+y)∈V，我们称为 V 对向量的加法封闭；对任意的标量 k∈V，向量 x∈V，都有 kx 属于 V，我们称 V 对标量与向量的乘法封闭。

如果 V 满足向量的加法和乘法封闭性，我们就称 V 是 F 上的向量空间。

向量空间除了满足这两个封闭性，还满足基本运算法则，比如交换律、结合律、分配律等等。

向量之间的距离

向量空间中两个向量的距离，就是这两个向量所对应的点之间的距离。

曼哈顿距离（Manhattan Distance）

城市街区距离，

从 A 点到 B 点有多条路径，但是无论哪条，曼哈顿距离都是一样的。
二维：

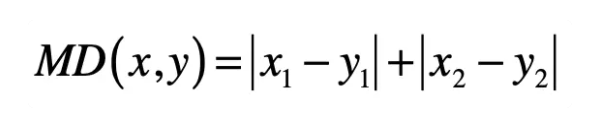
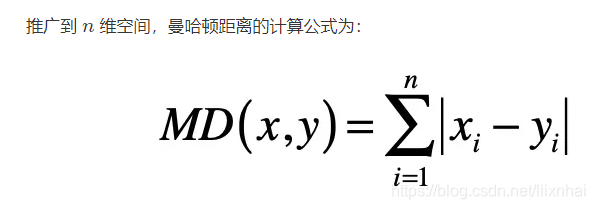
其中 n 表示向量维度，xi​ 表示第一个向量的第 i 维元素的值，yi​ 表示第二个向量的第 i 维元素的值。

欧氏距离（Euclidean Distance）

欧几里得距离，
指在 n 维空间中两个点之间的真实距离，

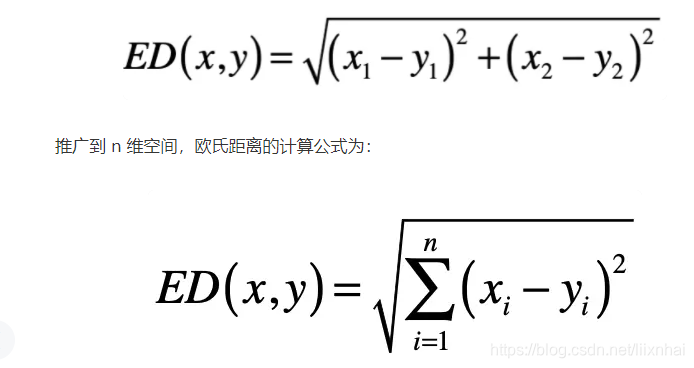
切比雪夫距离（Chebyshev Distance）

切比雪夫其实是在模拟国际象棋里国王的走法。国王可以走临近 8 个格子里的任何一个。
一开始，为了走尽量少的步数，国王走的一定是斜线，所以横轴和纵轴方向都会减 1，直到国王的位置和目标位置在某个轴上没有差距，这个时候就改为沿另一个轴每次减 1。所以，国王走的最少格子数是 ∣x1​−y1​∣ 和 ∣x2​−y2​∣ 这两者的较大者。

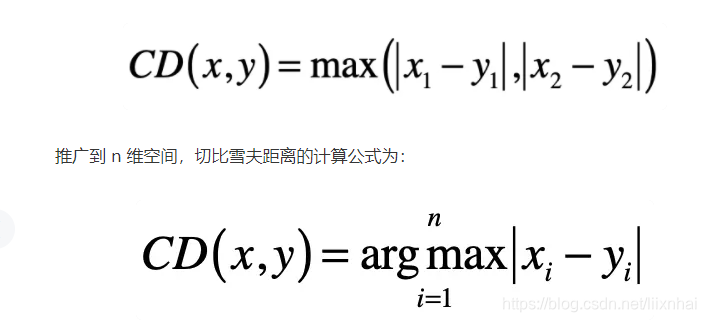
闵可夫斯基距离

闵氏距离

上述三种距离，都可以用一种通用的形式表示，就是闵氏距离。
在二维空间中，两个点 x(x1​,x2​) 与 y(y1​,y2​) 间的闵氏距离是：

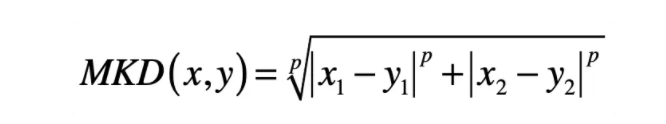
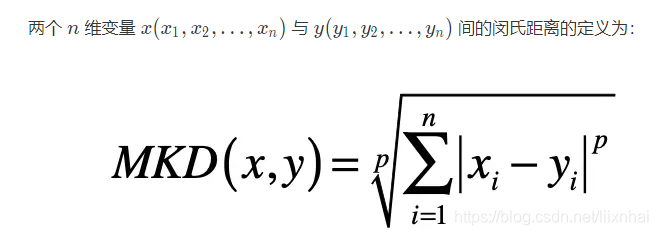
其中 p 是一个变参数，尝试不同的 p 取值，你就会发现：当 p=1 时，就是曼哈顿距离；当 p=2 时，就是欧氏距离；当 p 趋近于无穷大的时候，就是切比雪夫距离。这是因为当 p 趋近于无穷大的时候，最大的 ∣xi​−yi​∣ 会占到全部的权重。

距离可以描述不同向量在向量空间中的差异，所以可以用于描述向量所代表的事物之差异（或相似）程度。

向量的长度

向量的长度，也叫向量的模，是向量所对应的点到空间原点的距离。
通常我们使用欧氏距离来表示向量的长度。

“范数”

范数满足非负性、齐次性、和三角不等式
范数常常被用来衡量某个向量空间中向量的大小或者长度。
L1​ 范数 ∣∣x∣∣ ，它是为 x 向量各个元素绝对值之和，对应于向量 x 和原点之间的曼哈顿距离。
L2​ 范数 ∣∣x∣∣2​ ，它是 x 向量各个元素平方和的 21​ 次方，对应于向量 x 和原点之间的欧氏距离。
Lp​ 范数 ∣∣x∣∣p​ ，为 x 向量各个元素绝对值 p 次方和的 1/p 次方，对应于向量 x 和原点之间的闵氏距离。
L∞​ 范数 ∣∣x∣∣∞​ ，为 x 向量各个元素绝对值最大那个元素的绝对值，对应于向量 x 和原点之间的切比雪夫距离。

向量之间的夹角

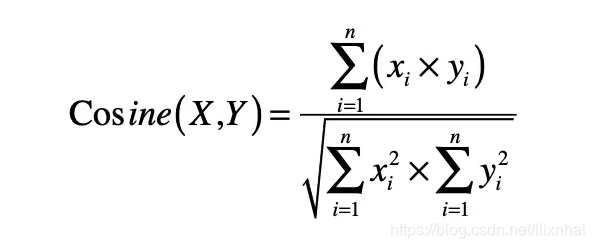
分子是两个向量的点乘，而分母是两者长度（或 L2 范数）的乘积，
L2 范数可以使用向量点乘自身的转置来实现。

向量空间模型（Vector Space Model）

向量空间模型假设所有的对象都可以转化为向量，然后使用向量间的距离（通常是欧氏距离）或者是向量间的夹角余弦来表示两个对象之间的相似程度。
由于夹角余弦的取值范围已经在 -1 到 1 之间，而且越大表示越相似，所以可以直接作为相似度的取值。相对于夹角余弦，欧氏距离 ED 的取值范围可能很大，而且和相似度呈现反比关系，所以通常要进行 1/(ED+1) 这种归一化。
当 ED 为 0 的时候，变化后的值就是 1，表示相似度为 1，完全相同。当 ED 趋向于无穷大的时候，变化后的值就是 0，表示相似度为 0，完全不同。所以，这个变化后的值，取值范围是 0 到 1 之间，而且和相似度呈现正比关系。

向量空间模型，可以用在K 近邻（KNN）分类、K 均值（K-Means) 聚类等基于相似度的机器学习算法中。