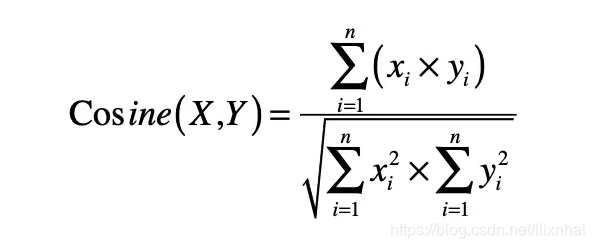文章目录
- 向量空间模型(Vector Space Model)
- 0. 概述
- 1. TF(Term frequency ,TF)
- 2. IDF(Inverse document frequency,IDF)
- 3. TF-IDF(Term Frequency-Inverse Document Frequency)
- 4. Similarity Function 相似性函数
- 5. 举例
- 举例1:文献中的tf-idf
- 举例2:完整的代码以及谷歌搜索攥取分析
- 举例3:在图像领域的使用
向量空间模型(Vector Space Model)
参考文献:
tf-idf原理以及应用
coursera:Vector Space Model
Tf-idf and Cosine Similarity
向量空间模型
0. 概述
向量空间模型(Vector Space Model)概念简单,把对文本内容的处理简化为向量空间中的向量运算,并且它以空间上的相似度表达语义的相似度,直观易懂。当文档被表示为文档空间的向量,就可以通过计算向量之间的相似性来度量文档间的相似性。文本处理中最常用的相似性度量方式是余弦距离。
我们在对文本内容操作分析之前,我们先要明确几个概念(参考连接)
- 文档(Document):泛指一般的文本或者文本中的片断(段落、句群或句子)。一般指一篇文章,尽管文档可以是多媒体对象,但是以下讨论中我们只认为是文本对象,本文对文本与文档不加以区别。(最后的章节会有拓展)
- 项(Term):文本的内容特征常常用它所含有的基本语言单位(字、词、词组或短语等)来表示,这些基本的语言单位被统称为文本的项,即文本可以用项集(Term List)表示为
D(T1,T2,...,Tn)其中是Tn是项,1≤k≤n - 项的权重(Term Weight):对于含有n个项的文本
D(T1,T2,...,Tn),项常常被赋予一定的权重表示他们在文本D中的重要程度,即 D=D(T1,W1;…;Tn, Wn)。这时我们说项的权重Wk(1≤k≤n)。 - 向量空间模型(VSM):给定一文本D=D(T)由于在文本中既可以重复出现又应该有先后次序的关系,分析起来有一定困难。为了简化分析,暂时不考虑的顺序,并要求互异,这时可以把,D看作是一个n维的坐标(向量),而Wn就是n维坐标所对应的值,所以文档D就可以被看作一个n维的向量了。
- 相似度(Similarity):两个文本D、Z。D、Z之间的(内容)相关程度(Degree of Relevance)常常用他们之间的相似度Sim(D,Z)来度量,当文本被表示为向量空间模型时,我们可以借助与向量之间的某种距离来表示文本间的相似度常用向量之间的内积进行计算,或者用夹角的余弦值表示:
可以看出,对向量空间模型来说,有两个基本问题:即特征项的选择和项的权重计算。(关于特征项的选择,前面给出的参考博客中给出了比较详尽的描述,这里不做重点讨论,有时间再作为补充补上,我们重点讨论项的权重计算)
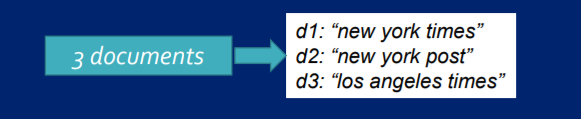
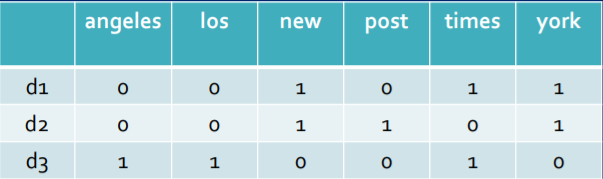
下面就用一个例子,来对项的权重计算进行描述。我们手里有三个文档,分别是d1、d2、d3,内容如下所示,我们希望通过某种方法来描述三个文档之间的关系和相似性,我们便可以进行以下的操作。
1. TF(Term frequency ,TF)
词频 (term frequency, TF) 指的是某一个给定的词语(项)在该文件中出现的次数。这个数字通常会被归一化(一般是词频除以文章总词数), 以防止它偏向长的文件。(同一个词语在长文件里可能会比短文件有更高的词频,而不管该词语重要与否。)
但是, 需要注意, 一些通用的词语对于主题并没有太大的作用, 反倒是一些出现频率较少的词才能够表达文章的主题, 所以单纯使用是TF不合适的。权重的设计必须满足:**一个词预测主题的能力越强,权重越大,反之,权重越小。**所有统计的文章中,一些词只是在其中很少几篇文章中出现,那么这样的词对文章的主题的作用很大,这些词的权重应该设计的较大。IDF就是在完成这样的工作.
- 计算该词条在文件集中出现的次数
2. IDF(Inverse document frequency,IDF)
逆向文件频率 (inverse document frequency, IDF) IDF的主要思想是:如果包含词条t的文档越少, IDF越大,则说明词条具有很好的类别区分能力。某一特定词语的IDF,可以由总文件数目除以包含该词语之文件的数目,再将得到的商取对数得到。
计算公式如下:
I D F = l o g 2 ( n / t e r m c o u n t ) IDF=log_2(n/termcount) IDF=log2(n/termcount)
其中n表述所有文件集文档的数目(这里指的3),termcount 是词条在所有文件中出现的次数(即tf),特别的,一说分母为termcount+1,以其可能造成分母为0 的情况

- **NOTE:**为什么这里使用2做底数呢?实际上没有可论证的理由,一种比较有道理的说法是,在计算机领域很多数字都与2的次方有关系。而且IDF的数值与log的底数没有直接的关系,因为
log_2(x)=lg(x)*lg2,而显然的,lg2是一个常数,所以对于我们的分析没有较大的差别
3. TF-IDF(Term Frequency-Inverse Document Frequency)
- 我们为什么要TF-IDF?
一个例子:假设100篇文档有10000个词,研究某篇500词文章,“机器学习”出现了20次,“而且”出现了20次,那么他们的TF都是20/500=0.04。再来看IDF,对于语料库的100篇文章,每篇都出现了“而且”,因此它的IDF就是log1=0,他的TFIDF=0。而“机器学习”出现了10篇,那么它的IDF就是log10=1,他的TF-IDF=0.04>0,显然“机器学习”比“而且”更加重要。
上述例子其实也在告诉我们,我们应该构建一种比较公平的权重,来更加均衡的反映Term的状况。TF-IDF出现的原因也正是如此。
某一特定文件内的高词语频率,以及该词语在整个文件集合中的低文件频率,可以产生出高权重的TF-IDF。因此,TF-IDF倾向于过滤掉常见的词语,保留重要的词语。
综合以上,我们使用TF-IDF来对核心词进行评估,计算方法为:
T F − I D F = T F ∗ I D F TF-IDF=TF*IDF TF−IDF=TF∗IDF
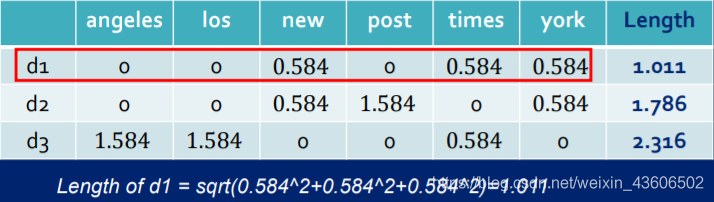
(这里也给出了直接计算距离Length的方法来描述两个文件的相似程度,相似程度函数有很多,我们一般使用的是余弦函数,下面我们将介绍这种相似性函数)
4. Similarity Function 相似性函数
From each document we derive a vector.The set of documents in a collection then is viewed as a set of vectors in a vector space. Each term will have its own axis. Using the formula given below we can find out the similarity between any two documents.
- 使用Cosine函数,计算公式如下:
S i m i l a r i t y = c o s ( θ ) = A ∗ B ∣ ∣ A ∣ ∣ ∗ ∣ ∣ B ∣ ∣ = ∑ i = 1 n A i B i ( ∑ i = 1 n A i 2 ) ( ∑ i = 1 n B i 2 ) Similarity=cos(\theta)=\frac{A*B}{||A||*||B||}=\frac{\sum_{i=1}^{n}{A_iB_i}}{\sqrt(\sum_{i=1}^{n}{A_i^2})\sqrt(\sum_{i=1}^{n}{B_i^2})} Similarity=cos(θ)=∣∣A∣∣∗∣∣B∣∣A∗B=(∑i=1nAi2)(∑i=1nBi2)∑i=1nAiBi

5. 举例
举例1:文献中的tf-idf
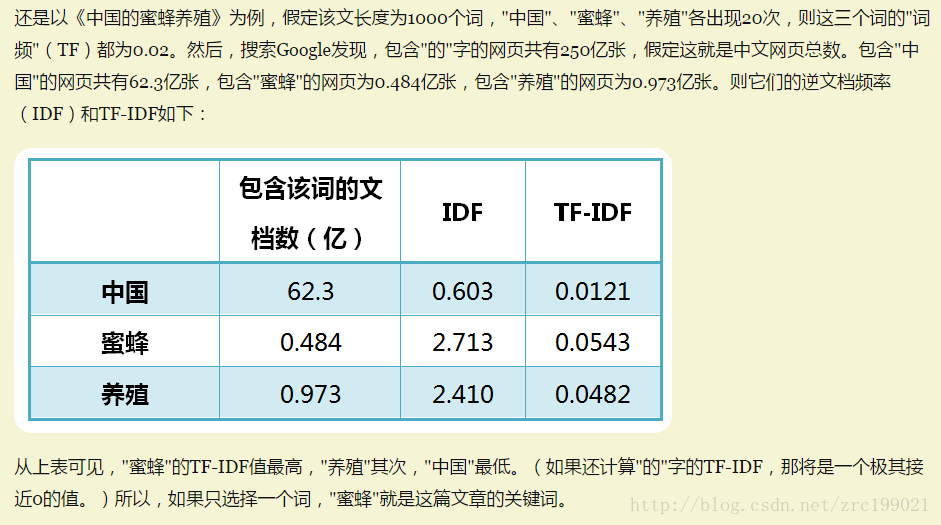
举例2:完整的代码以及谷歌搜索攥取分析
举例3:在图像领域的使用
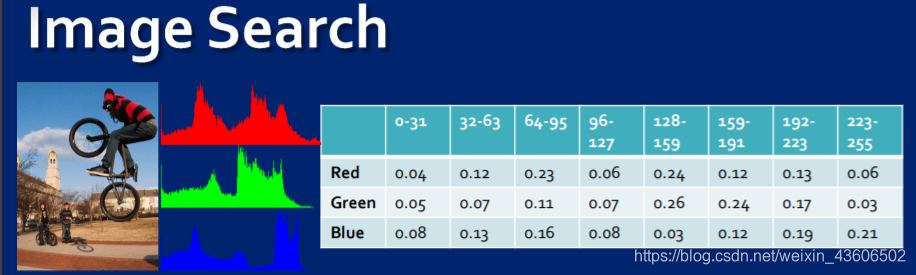
目前常用向量空间模型对图像进行相似度搜索。人们可以从图像中计算未来。一个常见的特征是散点直方图。考虑一下这里的图像。可以创建红、绿、蓝通道的直方图,其中直方图是具有一定密度值的像素数。这张图片大部分是亮的,所以暗像素的数量相对较小。现在我们可以把直方图看作一个向量。通常,像素值在创建矢量之前会发生弯曲。表中显示的是一个特征向量,其中每一行的数字都与图像的大小进行了标准化,使行和等于1。类似的向量可以计算图像纹理、物体形状和任何其他属性。因此,向量空间模型对非结构化数据具有重要意义。
一行的数字都与图像的大小进行了标准化,使行和等于1。类似的向量可以计算图像纹理、物体形状和任何其他属性。因此,向量空间模型对非结构化数据具有重要意义。