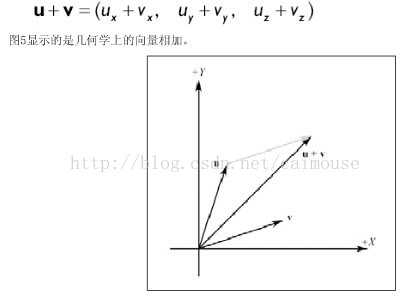
• 向量空间：如果在一个空间中，任取若干个向量进行相加或数乘，其计算结果仍然在该空间中，则称这个空间为向量空间。换句话说，向量空间对于相加和数乘运算是封闭的(closed)。

        当然，基于向量的广义定义，全部2*2的实数矩阵也是一个向量空间，记作M。

• 子空间：在一个向量空间V中，如果存在一个空间S，其中任取若干个向量进行相加或数乘，其计算结果仍然在空间S中，则该空间S称为向量空间V的子空间。

         子空间有一个特点：由于其满足数乘封闭性，任一子空间必然包括零向量。直观而言，子空间必然是向量空间   中一个穿过原点的“平面”。

• 矩阵A的列空间(Column space) C(A)：矩阵A中列向量的所有线性组合，构成矩阵A的列空间。
• 矩阵A的零空间(Nullspace) N(A)：满足Ax=0的所有解集合，构成矩阵A的零空间。

 

1、正交性

正交矩阵:如果AAT=E（E为单位矩阵，AT表示“矩阵A的转置矩阵”）或ATA=E，则n阶实矩阵A称为正交矩阵。

• 向量正交：如果两个向量的内积为零，则两个向量正交，即

                                                                                       

       子空间正交：给定两个子空间S、T，若S中的所有向量与T中的所有向量都正交，则称子空间S和T正交。

• 正交补(Orthogonal complement)：

• 子空间V的正交补是一个包含了所有与V正交的向量的子空间，记作

 

 它们的一些性质可以由下图很好的总结：

注意，图中下方的dimension分别是 n-r 和 m-r。

        其中，有几点值得关注的地方：

• 矩阵A行空间的维度与列空间相同，都等于矩阵的秩 r。我们来看看为什么：

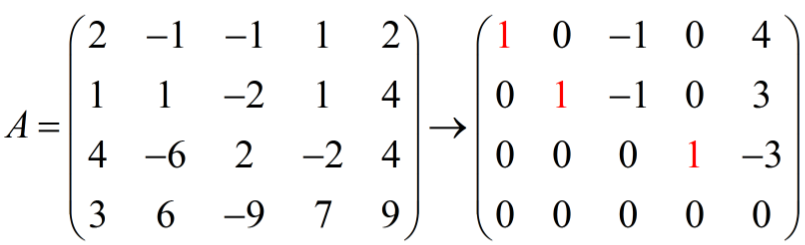
        首先看行空间。需要指出的是，矩阵A经过消元后得到最简形式R，这个过程是通过行变换实现的，即行向量的线性组合，因此不会改变矩阵A的行空间，即。而行空间是由行向量线性组合而成，因此R中的非零行的线性组合可以生成行空间，其个数为主元个数，即为矩阵的秩r。另外，我们也找到了矩阵A行空间的基，即R中r个主元所在的行（非零行）。

 

         再来看列空间。需要指出的是，经过行变换后，矩阵A的列空间已经发生改变，即。但是，它们具有相同的零空间，即具有相同使列向量组合为零的组合，因此相对应的r个主列都是独立。所以矩阵A的列空间的维度也是矩阵的秩r，列空间的基为A中的主列（注意不是R中的！）。

• 矩阵A零空间的维度为n-r，左零空间的维度为m-r。这是为什么呢？它们的基又是什么呢？

        先来看零空间。矩阵A零空间的维度等于自由变量的个数，因此为n-r。由3.2小节可以看到，零空间由特殊解的线性组合得到，因此零空间的基即为n-r个特殊解。

        再来看左零空间。为什么被称为左零空间？很显然，因为它是满足

 

的解构成的空间。左零空间的维度类比于零空间。由于

 

，因此

，即维度为m-r。左零空间的基可以通过下面方法得到：

        对矩阵A消元时我们有消元矩阵E满足：

 

，对应3.2小节中的矩阵A，即：

        

         因为我们要找的就是使矩阵A行向量的线性组合为零的组合，因此R中的零行所对应的E中的行向量（上例中的行3）即为左零空间的基。总而言之，矩阵A左零空间的基为：与R中的m-r个零行所对应的E中的行向量。

• 生成(Span)空间：向量生成了一个空间，意味着该空间由这些向量的全部线性组合组成。如：矩阵A的列向量生成了矩阵A的列空间。

 

• 基(Basis)：一个空间的基，是具有以下两个性质的一组向量：1、线性独立；2、能够生成这个空间。换句话说，一个空间的基便是能够生成该空间的“最小”的向量集合。
• 维度(Dimension)：一个空间的维度，是该空间的基中向量的个数。因此，对于一个空间，其基向量可以不同，但其数量必定是一样的。

• 矩阵的秩(Rank)：为了概念的完整性，我们提前说明一下矩阵的秩，这是矩阵一个非常重要的量，记作 rank(A)=r。秩的理解有以下几种不同的角度，但他们其实都在说同一个概念：

        1、矩阵的秩等于消元后矩阵的主列(pivot columns)的个数：r = # pivot columns；

        2、矩阵的秩等于矩阵A列空间的维度：r = dim C(A)；