简介

splay的原名是伸展树，一种超级实用的数据结构，能快速地干很多数据结构不能干的事情。
很久以前就听说过并且略微地学了一些，但是当时了解地并不是很多。
有些人把splay达成spaly叫做死吧你，(⊙﹏⊙)b

结构

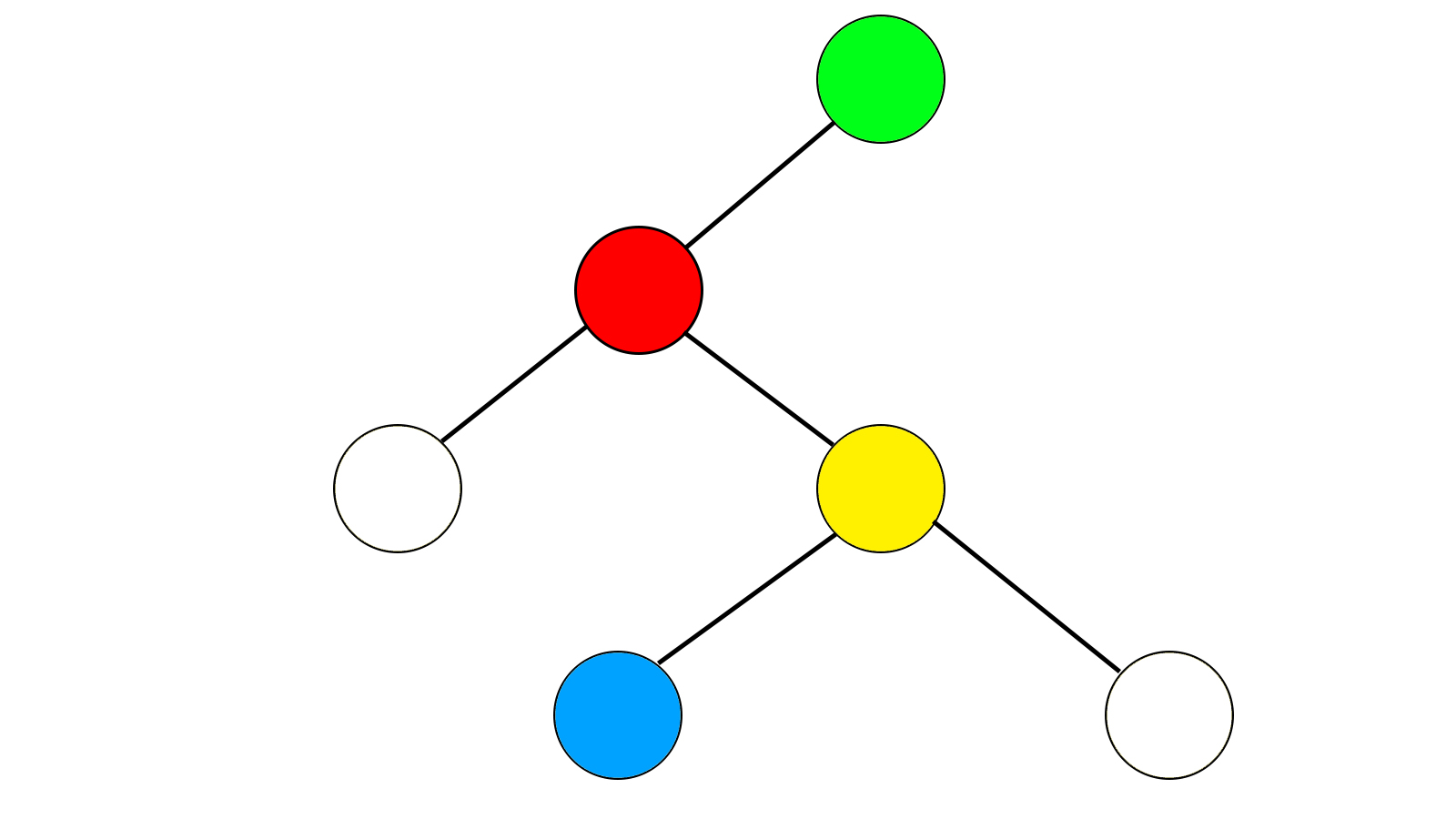
实质上他是一个二叉搜索树，就是每个节点的左儿子在原序列中是在自己左边的，右儿子在原序列中是在自己右边的，构图的方式有很多。
每一个节点都可以存储一些值，表示它的子树中的信息（比如说什么最大值啊，和啊之内的）。

构图

fo(i,1,n){scanf("%d",&a[i+1]);f[i]=i+1;t[i+1][0]=i;update(i+1);}f[n+1]=root=n+2,t[n+2][0]=n+1;update(n+2);

初学者的构图可以构成一条链。这样很明显左儿子在原序列上的位置是在自己左边的了。

但是有一个很奇妙的问题，为什么从2号点开始建？为什么建完点还要再向上多开一个n+2号点？

其实这种打法可以避免后面的特判，现在的1号点和n+2号点是建立在首尾两段的，如果不建立这两个点2号点的儿子和n+1号点的父亲都会指向0并传递信息，但是首尾建立一个虚点在修改操作中可以更方便的操作。比如说旋转的时候要涉及到首尾的时候，如果没有虚点，无法把首尾单独放到一个子树中去。

其实建成一条链在后面的操作会很慢。

int build(int l,int r,int y){if(l>r)return 0;int mid=(l+r)/2;int x=insert(a[mid]);f[x]=y;if(l==r)return x;tt[x][0]=build(l,mid-1,x);tt[x][1]=build(mid+1,r,x);update(x);return x;
}
root=build(0,n+1,0);

insert是建点操作，到后面再讲。
这样一开始就建成一颗二叉树会比较快。

功能

旋转

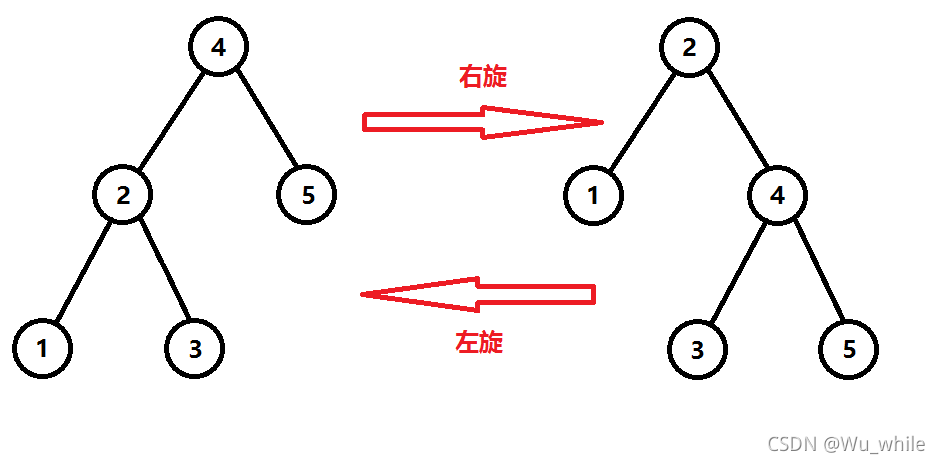
首先讲一个重要的部分，就是旋转。

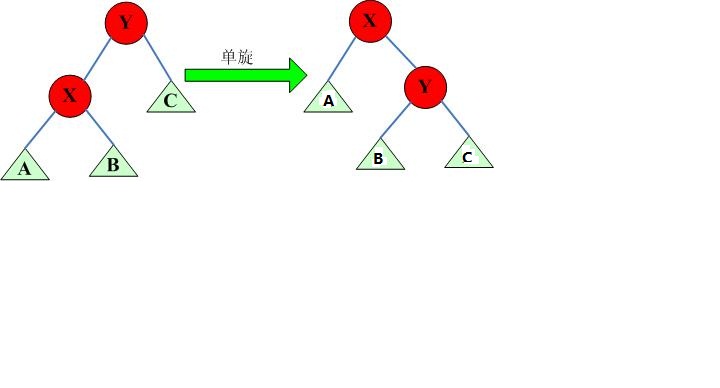
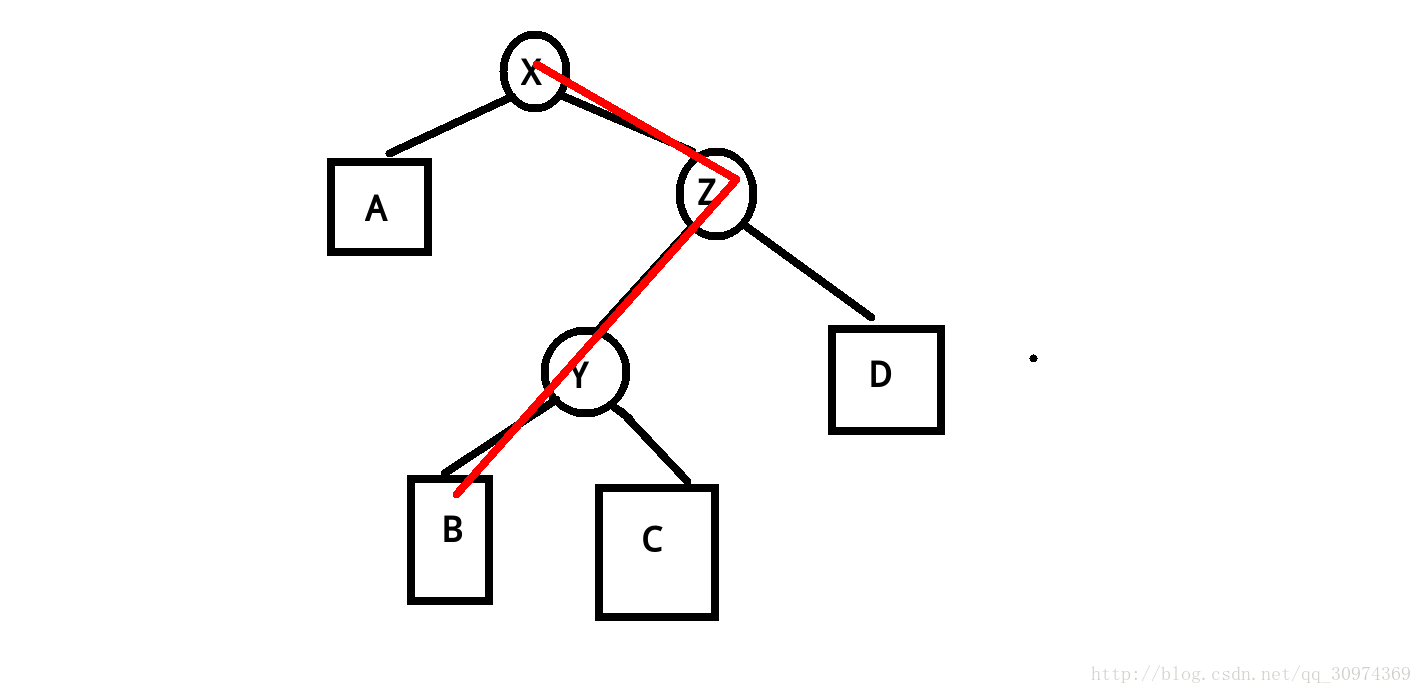
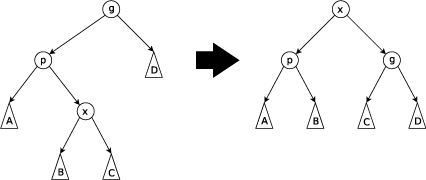
其实splay这颗二叉树的中序遍历就是原序列，例如图中的原序列就是：AXBYC。现在我们要把x旋转到y的位置上，但是不能改变这棵树的中序遍历（及在原序列的先后顺序）。

bool son(int x){if(tt[f[x]][0]==x)return 0;return 1;
}
void rotate(int x){int y=f[x],z=son(x);tt[y][z]=tt[x][1-z];if(tt[x][1-z])f[tt[x][1-z]]=y;f[x]=f[y];if(f[y])tt[f[y]][son(y)]=x;f[y]=x;tt[x][1-z]=y;update(y);update(x);
}

其实代码很短(f[x]表示x的父亲，tt[x][0]和tt[x][1]分别是x的左右儿子)。
函数son(x)的作用是分辨x是其父亲的左儿子还是右儿子(左儿子是0，右儿子是1)。
当把x旋转到y是，y就成为的x的右儿子，但是x原来的右儿子B就没有地方放了。怎么办？我们发现在原序列中的顺序是X < B < Y， 所以B应该在X的右边但是在Y的左边，所以现在Y的左儿子应该是B右儿子不变。如图所示。
代码运用了一个小技巧z和1-z刚好把0和1转化，也可以打成z和z^1（是xor，异或）。

将x节点旋转为y节点的儿子

void splay(int x,int y){if(x==y)return;remove(x,y);while(f[x]!=y){if(f[f[x]]!=y)if(son(f[x])==son(x))rotate(f[x]);else rotate(x);rotate(x);}if(!y)root=x;
}

remove是懒标记下传，后面再讲。
为什么是把x旋转为y的儿子，因为这样更加方便的操作，比如说要对x的子树进行操作，如果变成把x旋转到y的位置会麻烦很多而且不方便打。
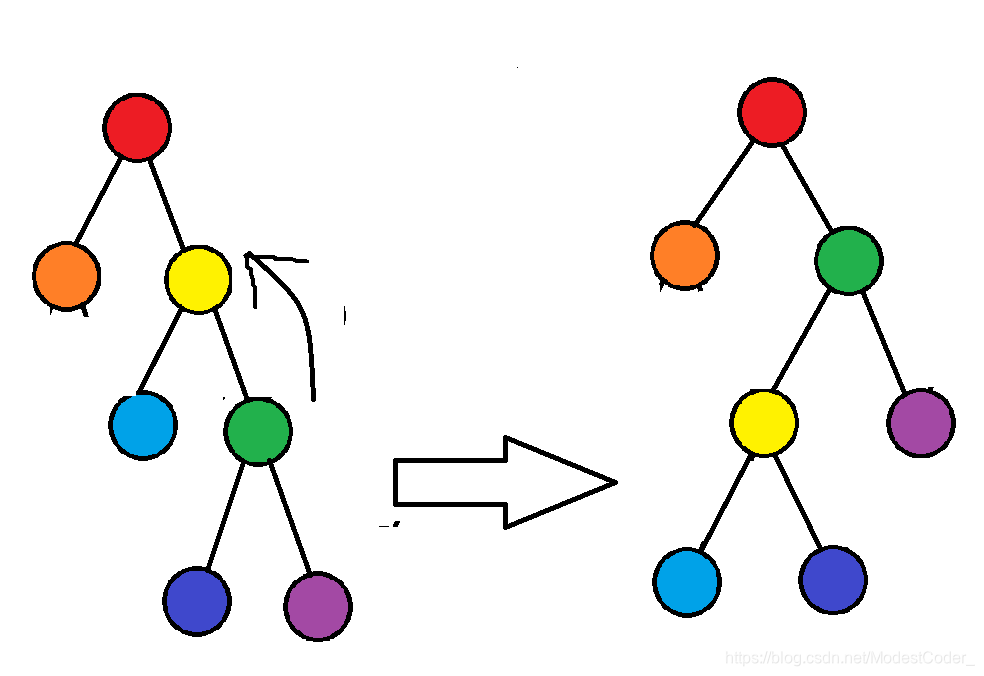
旋转的思路：如果x和x的父亲和x的爷爷是一条折线，那么就旋转成不是一个折线，然后像上面将的旋转一样向上推进。具体的最好自己画个图，有利于理解。
一般像splay(x,0)就是把x旋转为根节点，splay(x,y)就是把x旋转为y的儿子(具体是左儿子还是有儿子根据原序列中的顺序来定)

节点值的更新

void update(int x){if(!x)return;t[x].size=1+t[tt[x][0]].size+t[tt[x][1]].size;t[x].sum=key[x]+t[tt[x][0]].sum+t[tt[x][1]].sum;t[x].lda=max(t[tt[x][0]].lda,t[tt[x][0]].sum+key[x]+t[tt[x][1]].lda);t[x].rda=max(t[tt[x][1]].rda,t[tt[x][1]].sum+key[x]+t[tt[x][0]].rda);t[x].mx=max(max(t[tt[x][0]].mx,t[tt[x][1]].mx),t[tt[x][0]].rda+t[tt[x][1]].lda+key[x]);}

当x节点的子节点变动是就需要更新，具体更新的内容据题目而定。

对于一段节点进行操作

x=kth(root,l-1);splay(x,0);
y=kth(root,r+1);splay(y,x);

如果要对[l,r]这段区间进行操作。思路：先把这段区间同时放到一颗子树上去且这可子树没有其他多余的节点。
首先如果把l-1旋转成根节点，那么[l,n]的节点都会在l-1(及root)的右子树上。然后再把r+1旋转为l-1的儿子，因为r+1在序列中再l-1的右边，所以r+1旋转之后一定是l-1的右儿子，那么在原序列中的顺序大于l-1的，小于r+1一定都是现在r+1节点的左子树了。
那么现在只要对r+1的左子树进行操作就好了。

     printf("%d\n",t[tt[y][0]].mx);

比如要输出[l,r]段的最大值，上段程序后面只用加上这段程序就可以了。

插入一个或者一段节点

现在要把a数组中的数从posi位置后开始插入进序列中。
参照对于一段节点进行操作。

     fo(i,1,k)scanf("%d",&a[i]);x=kth(root,posi);splay(x,0);y=kth(root,posi+1);splay(y,x);tt[y][0]=build(1,k,y);

现在只需要把这k个数插进y的左子树中就可以了。build就是上面构图中的build，实质就是把a数组1到k中的节点插为y的子树。

删除一个或者一段节点

现在要从posi这个位置开始删去k个节点。
参照对于一段节点进行操作。

    scanf("%d%d",&posi,&k);posi++;x=kth(root,posi-1);splay(x,0);y=kth(root,posi+k);splay(y,x);del(tt[y][0]);tt[y][0]=0;update(y);update(x);

这里也同理，因为要从posi开始删节点，序列的位置要比posi-1大，比posi+k小。
del函数是什么呢？

void del(int x){if(!x)return;shan[++shan[0]]=x;del(tt[x][0]);del(tt[x][1]);
}

因为删去了一些点，这些点原来的位置不能浪费在那里，用一个栈存起来，建点的之后再用。

建点操作

int insert(int x){int o;if(shan[0])o=shan[shan[0]--];else o=++num;//主要是这行初始化.例如:key[o]=t[o].sum=t[o].mx=x;t[o].size=1;根据题目而定..
}

为了防止空间的浪费，如果还有删除过得节点的位置空在那里的话，就调用出来，否则就新建一个位置。

区间的修改操作

例如从posi开始后的k个点都加上k，参照对于一段节点进行操作。

x=kth(root,posi-1);splay(x,0);
y=kth(root,posi+k);splay(y,x);
change(tt[y][0],zhi);
update(y);update(x);

同理。

void change(int x,int y){//这里打的是区间加操作，据题目而定if(!x)return;t[x].sum+=t[x].size*y;key[x]+=y;t[x].add+=y;//add是懒标记，用于标记下传if(y>0)t[x].lda=t[x].rda=t[x].mx=t[x].sum;//这里是某道题的修改，据题目而定else t[x].lda=t[x].rda=0,t[x].mx=y;    
}

懒标记下传

void down(int x){if(!x)return;if(t[x].add!=maxn){change(tt[x][0],t[x].add);change(tt[x][1],t[x].add);t[x].add=maxn;}
}

void remove(int x,int y){do{d[++d[0]]=x;x=f[x];}while(x!=y);while(d[0])down(d[d[0]--]);
}

这种东西支持区间修改的数据结构都要用到的，但是splay中的有所不同，因为只有在旋转的之后才用的到，例如splay(x,y)，所以需要把x到y的路径上的标记都下传。

区间翻转操作

例如把x的子树的区间翻转。

void overturn(int x){if(!x)return;swap(tt[x][0],tt[x][1]);t[x].biao^=1;
}

其实很简单，只需要把所有节点的左右儿子调换即可。注意懒标记的biao要用^或者1-biao，因为如果某段区间被同时翻转两次相当于没有翻转。

查询序列中第k个位置

int kth(int x,int k){down(x);if(t[tt[x][0]].size+1==k)return x;if(t[tt[x][0]].size+1>k)return kth(tt[x][0],k);else return kth(tt[x][1],k-t[tt[x][0]].size-1);
}

这个很简单啦。
其实如果想知道第x节点在序列中的序号的话，可以把x旋转到根(及splay(x,0))，然后t[tt[x][0]].size+1就是x在原序列中的序号。

区间分离

把x为根节点的这棵树以原序列序号y为分水岭，分成l和r两颗子树。

void split(int x,int y,int &l,int &r){int j=kth(x,y);splay(j,0);l=j,r=t[j][1];tt[l][1]=0;f[r]=0;update(j);
}

区间合并

把以x为根的树和以y为根的树合并为树l。
为什么要找到x树中第 size[x]大(及在原序列中序号最大的节点)的节点，因为在原序列中序号最大的节点没有右儿子，方便合并。

void merge(int x,int y,int &l){int j=kth(x,size[x]);splay(j,0);tt[j][1]=y;f[y]=j;update(j);l=j;
}

维护各种的树

比如说Link_Cut_Tree（及lct或动态树）…

由于本人是个蒟蒻

目前也只知道这么多了，但是这些操作在大部分题目中都够用了。

入门题

【CQOI2014】排序机械臂
【NOI2005】维护数列
什么最大值，排序也可以用splay来练练手。