【学习笔记】Splay

article/2025/11/9 15:47:28

普通平衡树

模板题链接

1、引入

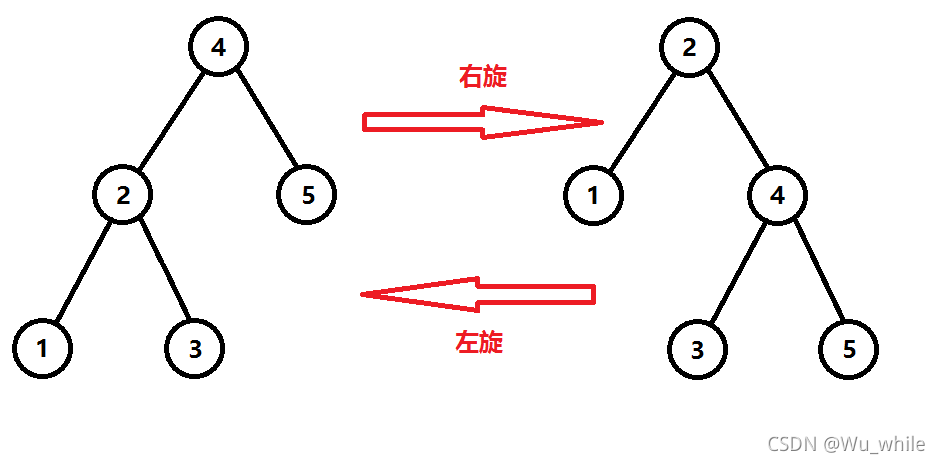
一种二叉树，这棵树满足任意一个节点，它的左儿子的权值<自己的权值<右儿子的权值
这种树叫做二叉查找树，这个概念应该在初赛中见过了吧

Splay就是利用这个结构来实现的

2、变量

模板题的7大变量

  • sz：表示当前节点个数
  • rt：表示当前根节点的编号
  • f[x]：表示编号x节点的父亲的编号
  • key[x]：表示编号为x的节点的对应的数值
  • size[x]：表示以编号为x的节点为根的子树的节点个数
  • recy[x]：表示以编号为x的节点的数值重复次数
  • son[x][0]/son[x][1]：表示以编号为x的节点的左/右儿子的编号

3、操作

清空一个节点
inline void clear(int x){f[x] = key[x] = size[x] = recy[x] = son[x][0] = son[x][1] = 0;//5个数组全部清零
}
确定一个节点是父亲的左儿子还是右儿子
int get(int x){return son[f[x]][1] == x;//如果自己是父亲的右儿子，返回1；否则返回0（0为左儿子，1为右儿子） 
}
更新一个节点
inline void update(int x){if (x){//如果这个点存在size[x] = recy[x];//自己重复的次数先累计if (son[x][0]) size[x] += size[son[x][0]];if (son[x][1]) size[x] += size[son[x][1]];//如果存在儿子，把儿子的size累积到自己//然后发现一个问题，更新自己的size时，必须保证儿子的size是正确的//所以后面的操作，当牵扯到儿子和父亲时，应该先更新新儿子，后更新新父亲}
}
把一个点连到另一点下面
void connect(int x, int y, int z){//x连到y下面，关系为z if (x) f[x] = y;//存在x，则x的父亲为y if (y) son[y][z] = x;//存在y，y的z关系儿子为x 
}
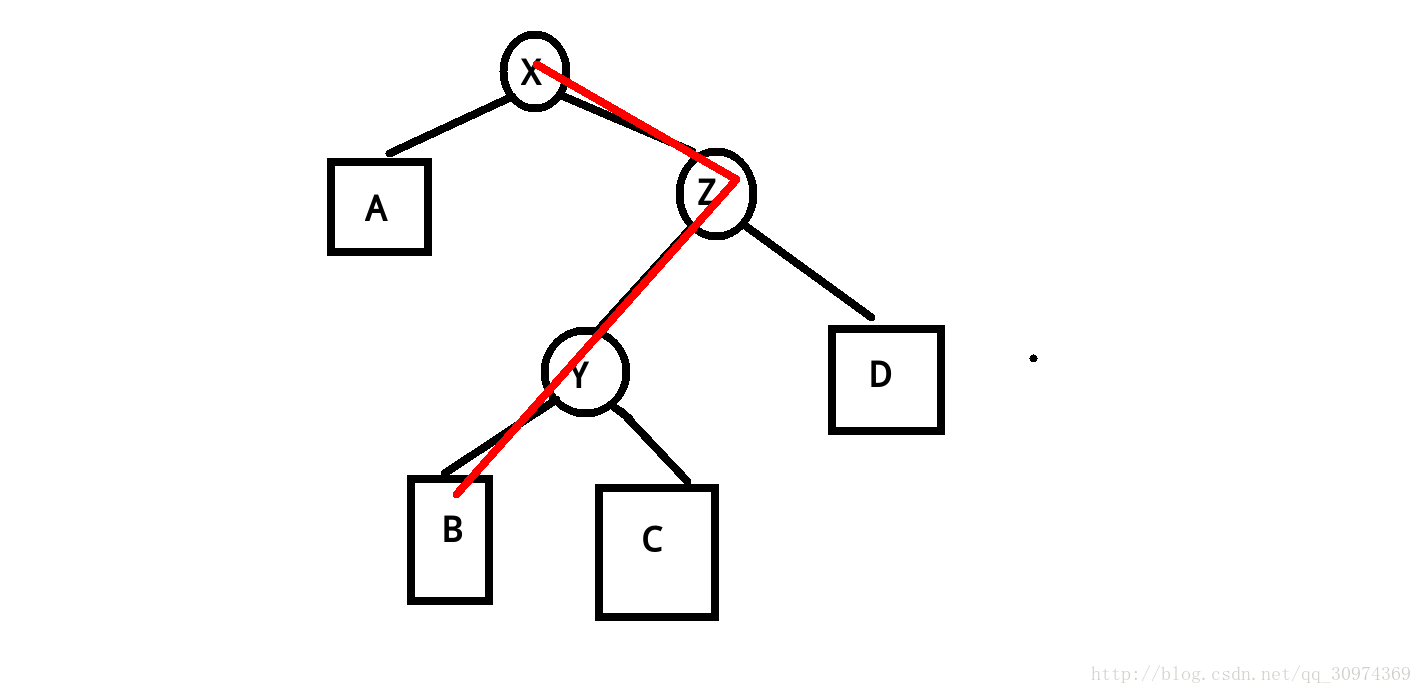
上旋

看图
情况1
发现：绿点上旋，绿点是父亲橙点的左儿子，所以绿点的右儿子紫点变成橙点的左儿子，橙点变成绿点的右儿子，绿点变成红点的左儿子
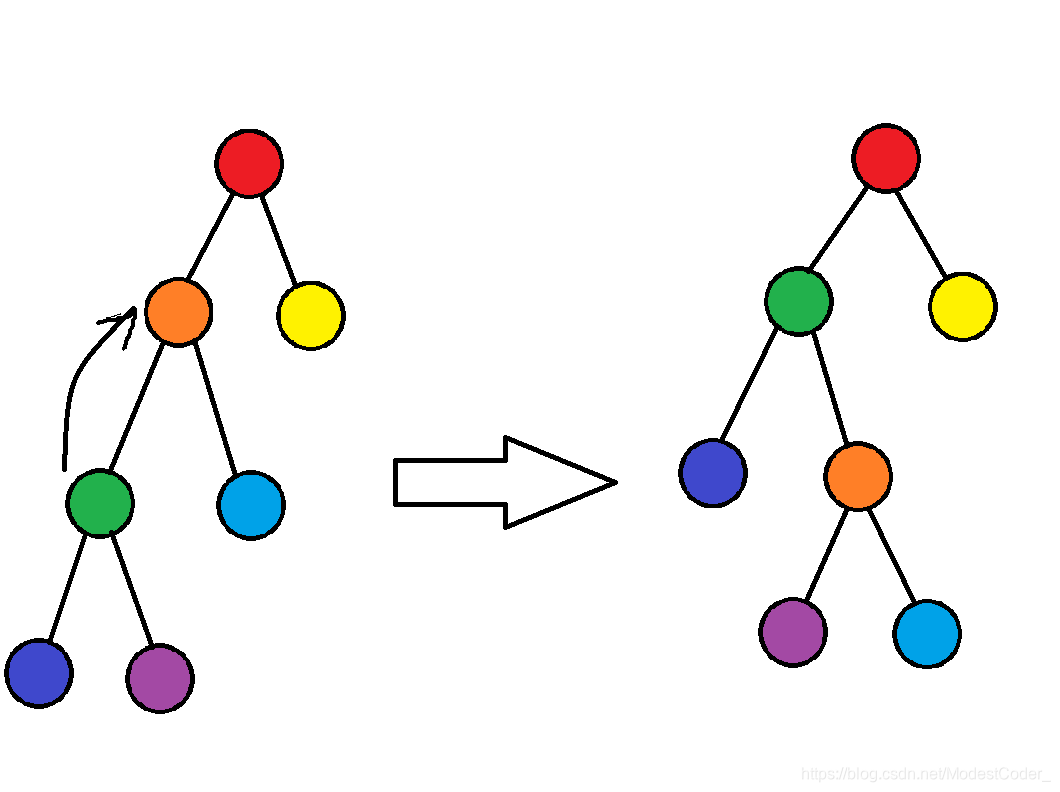
在这里插入图片描述
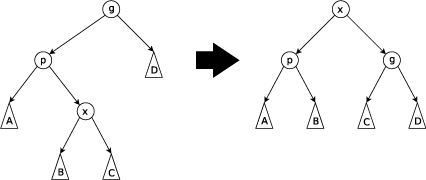
情况2
发现：绿点上旋，绿点是父亲黄点的右儿子，所以绿点的左儿子蓝点变成黄点的右儿子，黄点变成绿点的左儿子，绿点变成红点的右儿子

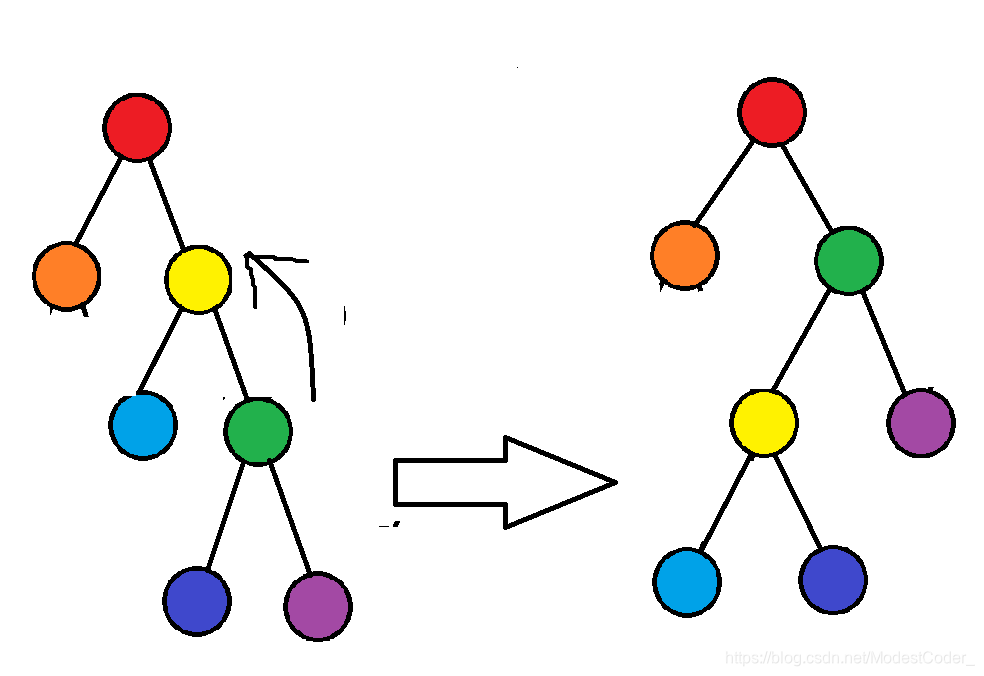
在这里插入图片描述
上面两种情况是有一种共同特点的
Code：

void rotate(int x){//上旋x int fa = f[x], ffa = f[fa], m = get(x), n = get(fa);//确定x，fa的关系 connect(son[x][m ^ 1], fa, m);//把要转的儿子(关系为m^1的儿子)转到父亲下，关系为m connect(fa, x, m ^ 1);//把父亲转到自己下面，关系为m^1 connect(x, ffa, n);//把自己转到父亲的父亲下，关系为n update(fa), update(x);//先更新fa，再更新自己，可以自己想想为什么是这个顺序 
}
splay

把一个点一直上旋，旋到规定点，此题全部是旋到根节点，所以默认旋到根节点
设当前splay的点为x
如果x的父亲是根，直接旋；
否则分两种情况：

  • get(x)=get(fa)，此时,先上旋fa，再上旋x
  • get(x)!=get(fa)，此时连续上旋两次x

为什么分两种情况？可以自行画图看一看
发现按照上述旋转，每次splay以后，整棵树十分的平衡！
（接近于完全二叉树）
如果不分情况，直接无脑上旋，则会结构变得比较乱

splay操作是算法的核心，它保证的二叉树的随机性，平衡性
所以，当你在打splay的时候，记住一条准则：有事没事splay一下

void splay(int x){for (int fa; fa = f[x]; rotate(x))//每次总是旋转自己 if (f[fa]) rotate(get(x) == get(fa) ? fa : x);//如果有爷爷（父亲的父亲），看父亲与父亲的父亲的关系决定转哪个 rt = x;//别忘了，把根赋为当前点 
}
插入一个点
void insert(int x){if (!rt){//树中没有一个节点 rt = ++sz;key[rt] = x;size[rt] = recy[rt] = 1;son[rt][0] = son[rt][1] = 0;//赋初值 return;}int now = rt, fa = 0;while (1){if (key[now] == x){//树中已有此点，重复+1 ++recy[now];update(now); update(fa);splay(now);//splay一下，保证平衡 return;}fa = now, now = son[now][x > key[now]];//满足二叉查找树的性质，往下跑 if (!now){++sz;key[sz] = x;size[sz] = recy[sz] = 1;//赋初值f[sz] = fa;//父亲是fa son[fa][x > key[fa]] = sz;//更新父亲的新儿子 update(fa);//更新父亲的size splay(sz);//splay一下，保证平衡return;}}
}
查询一个数的排名
int find(int x){//查排名 int now = rt, ans = 0;while (1){if (x < key[now]){now = son[now][0]; continue;//在左子树中 }ans += size[son[now][0]];//排名加上左子树节点个数 if (x == key[now]){ splay(now); return ans + 1; }//值等于当前点，splay一下，保证平衡，排名+1为当前排名 ans += recy[now];//排名加上当前节点的数的个数 now = son[now][1];//在右子树中 }
}
查询排名为k的数
int kth(int x){//查找排名为x的数 int now = rt;while (1){if (son[now][0] && x <= size[son[now][0]]){//在左子树中 now = son[now][0]; continue;}if (son[now][0]) x -= size[son[now][0]];//存在左儿子，排名减去左子树节点数 if (x <= recy[now]){ splay(now); return key[now]; }//说明就是当前点，splay一下，保证平衡，退出 x -= recy[now];//排名减去当前节点数的个数 now = son[now][1];//在右子树中 }
}
前驱、后继

采用全新的方法
首先，插入目标新节点，使该节点在根上
那么它的前驱为左子树中最大的那个
后继为右子树中最小的那个
最后，当然要删掉刚才插入的节点

至于为什么，想想就知道了

if (opt == 5){insert(x); printf("%d\n", key[pre()]); del(x);//insert->del}if (opt == 6){insert(x); printf("%d\n", key[nxt()]); del(x);//insert->del}

int pre(){//前驱为左子树中最大的那个 int now = son[rt][0];while (son[now][1]) now = son[now][1];return now;
}int nxt(){//后继为右子树中最小的那个 int now = son[rt][1];while (son[now][0]) now = son[now][0];return now;
}
删除一个点
void del(int x){int no_use = find(x);//find主要是把当前数的对应点找到，然后旋到根，返回值的排名在这里没用 if (recy[rt] > 1){//情况1：有重复，重复-1，更新，退出 --recy[rt];update(rt);return;}//接下来都是没有重复的情况 if (!son[rt][0] && !son[rt][1]){//情况2：没有儿子，直接清空 clear(rt);rt = 0;return;}if (!son[rt][0]){//情况3：没有左儿子，只有右儿子，右儿子变成根，清除自己 int tmp = rt;f[rt = son[rt][1]] = 0;clear(tmp);return;}if (!son[rt][1]){//情况4：没有右儿子，只有左儿子，左儿子变成根，清除自己 int tmp = rt;f[rt = son[rt][0]] = 0;clear(tmp);return;}//情况5：两个儿子都有，这是需要一个很简便的做法//把前驱splay到根，保持左子树其他节点不用动//原根右儿子变成前驱的右儿子//原根功成身退，清除掉//最后对前驱的size进行更新 int tmp = rt, left = pre();splay(left);connect(son[tmp][1], rt, 1);clear(tmp);update(rt);
}

4、模板题

全在上面了，直接Code：

#include <bits/stdc++.h>
#define maxn 100010
using namespace std;
int sz, rt, f[maxn], key[maxn], size[maxn], recy[maxn], son[maxn][2];inline int read(){int s = 0, w = 1;char c = getchar();for (; !isdigit(c); c = getchar()) if (c == '-') w = -1;for (; isdigit(c); c = getchar()) s = (s << 1) + (s << 3) + (c ^ 48);return s * w;
}void clear(int x){f[x] = key[x] = size[x] = recy[x] = son[x][0] = son[x][1] = 0;//5个数组全部清零
}int get(int x){return son[f[x]][1] == x;//如果自己是父亲的右儿子，返回1；否则返回0（0为左儿子，1为右儿子） 
}void update(int x){if (x){//如果这个点存在size[x] = recy[x];//自己重复的次数先累计if (son[x][0]) size[x] += size[son[x][0]];if (son[x][1]) size[x] += size[son[x][1]];//如果存在儿子，把儿子的size累积到自己//然后发现一个问题，更新自己的size时，必须保证儿子的size是正确的//所以后面的操作，当牵扯到儿子和父亲时，应该先更新新儿子，后更新新父亲}
}void connect(int x, int y, int z){//x连到y下面，关系为z if (x) f[x] = y;//存在x，则x的父亲为y if (y) son[y][z] = x;//存在y，y的z关系儿子为x 
}void rotate(int x){//上旋x int fa = f[x], ffa = f[fa], m = get(x), n = get(fa);//确定x，fa的关系 connect(son[x][m ^ 1], fa, m);//把要转的儿子转到父亲下，关系为m connect(fa, x, m ^ 1);//把父亲转到自己下面，关系为m^1 connect(x, ffa, n);//把自己转到父亲的父亲下，关系为n update(fa), update(x);//先更新fa，再更新自己，可以自己想想为什么是这个顺序 
}void splay(int x){for (int fa; fa = f[x]; rotate(x))//每次总是旋转自己 if (f[fa]) rotate(get(x) == get(fa) ? fa : x);//如果有爷爷（父亲的父亲），看父亲与父亲的父亲的关系决定转哪个 rt = x;//别忘了，把根赋为当前点 
}void insert(int x){if (!rt){//树中没有一个节点 rt = ++sz;key[rt] = x;size[rt] = recy[rt] = 1;son[rt][0] = son[rt][1] = 0;//赋初值 return;}int now = rt, fa = 0;while (1){if (key[now] == x){//树中已有此点，重复+1 ++recy[now];update(now); update(fa);splay(now);//splay一下，保证平衡 return;}fa = now, now = son[now][x > key[now]];//满足二叉查找树的性质，往下跑 if (!now){++sz;key[sz] = x;size[sz] = recy[sz] = 1;//赋初值f[sz] = fa;//父亲是fa son[fa][x > key[fa]] = sz;//更新父亲的新儿子 update(fa);//更新父亲的size splay(sz);//splay一下，保证平衡return;}}
}int find(int x){//查排名 int now = rt, ans = 0;while (1){if (x < key[now]){now = son[now][0]; continue;//在左子树中 }ans += size[son[now][0]];//排名加上左子树节点个数 if (x == key[now]){ splay(now); return ans + 1; }//值等于当前点，splay一下，保证平衡，排名+1为当前排名 ans += recy[now];//排名加上当前节点的数的个数 now = son[now][1];//在右子树中 }
}int kth(int x){//查找排名为x的数 int now = rt;while (1){if (son[now][0] && x <= size[son[now][0]]){//在左子树中 now = son[now][0]; continue;}if (son[now][0]) x -= size[son[now][0]];//存在左儿子，排名减去左子树节点数 if (x <= recy[now]){ splay(now); return key[now]; }//说明就是当前点，splay一下，保证平衡，退出 x -= recy[now];//排名减去当前节点数的个数 now = son[now][1];//在右子树中 }
}int pre(){//前驱为左子树中最大的那个 int now = son[rt][0];while (son[now][1]) now = son[now][1];return now;
}int nxt(){//后继为右子树中最小的那个 int now = son[rt][1];while (son[now][0]) now = son[now][0];return now;
}void del(int x){int no_use = find(x);//find主要是把当前数的对应点找到，然后旋到根，返回值的排名在这里没用 if (recy[rt] > 1){//情况1：有重复，重复-1，更新，退出 --recy[rt];update(rt);return;}//接下来都是没有重复的情况 if (!son[rt][0] && !son[rt][1]){//情况2：没有儿子，直接清空 clear(rt);rt = 0;return;}if (!son[rt][0]){//情况3：没有左儿子，只有右儿子，右儿子变成根，清除自己 int tmp = rt;f[rt = son[rt][1]] = 0;clear(tmp);return;}if (!son[rt][1]){//情况4：没有右儿子，只有左儿子，左儿子变成根，清除自己 int tmp = rt;f[rt = son[rt][0]] = 0;clear(tmp);return;}//情况5：两个儿子都有，这是需要一个很简便的做法//把前驱splay到根，保持左子树其他节点不用动//原根右儿子变成前驱的右儿子//原根功成身退，清除掉//最后对前驱的size进行更新 int tmp = rt, left = pre();splay(left);connect(son[tmp][1], rt, 1);clear(tmp);update(rt);
}int main(){int M = read();while (M--){int opt = read(), x = read();if (opt == 1) insert(x);if (opt == 2) del(x);if (opt == 3) printf("%d\n", find(x));if (opt == 4) printf("%d\n", kth(x));if (opt == 5){insert(x); printf("%d\n", key[pre()]); del(x);}if (opt == 6){insert(x); printf("%d\n", key[nxt()]); del(x);}}return 0;
}

5、小建议

建议完全理解splay的代码
多看看

不知道代码哪错了建议重构代码
建议过些天复习复习

文艺平衡树

模板题链接

1、引入

说白了，区间翻转

2、原理

发现一棵二叉查找树，中序遍历是有序的
既然这样，何不先按顺序加入二叉树？

对于每个操作 [ l , r ] [l,r] [l,r]，找到 k t h ( l − 1 ) , k t h ( r + 1 ) kth(l-1),kth(r+1) kth(l−1),kth(r+1)
分别记为 p r e , n x t pre, nxt pre,nxt
把 p r e pre pre旋到根，把 n x t nxt nxt旋到根的（右）儿子
发现： n x t nxt nxt的左子树节点集合= [ l , r ] [l,r] [l,r]节点集合
因为对于任何一个 x ∈ [ l , r ] x∈[l,r] x∈[l,r]，都有 v p r e < v x < v n x t v_{pre}<v_{x}<v_{nxt} vpre​<vx​<vnxt​
必定都在nxt左子树中，且nxt左子树没有别的节点

说明整个子树翻转一下就行啦

怎么做呢？采用打标记的方法
在nxt左儿子上打一个tag， t a g = 1 tag=1 tag=1说明这个区间需要翻转

下传标记，在每次求kth，splay的时候pushdown一下，反正能pushdown就pushdown，多了不会慢太多，少了万一wa了呢~~，其实自己分析一下也可以知道哪些需要pushdown，不过都下传保险嘛，万一分析错了呢

如何pushdown？首先儿子的tag^=1，至于为什么是亦或自己想想就行
然后交换两个儿子的编号（因为翻转），最后自己的tag=0

3、代码实现

首先，需要注意，插入-inf与inf，防止pre和nxt找不到

加入节点
    for (int i = 1; i <= n + 2; ++i) insert(i);//1~n全体+1，1为-inf，n+2为inf

void insert(int x){int now = rt, fa = 0;while(now) fa = now, now = son[now][x > key[now]];//插入新节点，知道可以插入为止now = ++sz;key[now] = x;f[now] = fa;if (fa) son[fa][x > key[fa]] = now;size[now] = 1;son[now][0] = son[now][1] = 0;splay(now, 0);//旋到根，保持平衡
}
上旋
void connect(int x, int y, int z){ f[x] = y, son[y][z] = x; }

void rotate(int x){int fa = f[x], ffa = f[fa], m = get(x), n = get(fa);connect(x, ffa, n);connect(son[x][m ^ 1], fa, m);connect(fa, x, m ^ 1);update(fa); update(x);
}

//注意这里的splay跟上面普通splay不一样
void splay(int x, int goal){int len = 0;for (int i = x; i; i = f[i]) q[++len] = i;for (int i = len; i; --i) pushdown(q[i]);//先把可能经过的节点全部下传一遍，注意下传顺序while (f[x] != goal){//没旋到goalint fa = f[x];if (f[fa] != goal) rotate(get(x) == get(fa) ? fa : x);rotate(x);}if (!goal) rt = x;//是不是旋到根节点
}
kth
int kth(int x){ int now = rt;while (1){ pushdown(now);//下传标记if (size[son[now][0]] >= x) now = son[now][0]; else{x -= size[son[now][0]];if (x == 1) return now;--x, now = son[now][1]; }}
}
翻转

翻转区间 [ l , r ] [l,r] [l,r]

void work(int l, int r){l = kth(l); r = kth(r + 2);//找到pre,nxtsplay(l, 0); splay(r, l);//上旋tag[son[r][0]] ^= 1;//打标记，注意这里也是亦或
}
下传标记
void pushdown(int x){if (tag[x]){//如果有标记tag[x] = 0;//自己变为0tag[son[x][0]] ^= 1;tag[son[x][1]] ^= 1;//下传swap(son[x][0], son[x][1]);//翻转儿子}
}
输出
void write(int x){pushdown(x);//下传if (son[x][0]) write(son[x][0]);//中序遍历 左中右if (key[x] > 1 && key[x] < n + 2) printf("%d ", key[x] - 1);//注意一开始都+1，最后-1if (son[x][1]) write(son[x][1]);
}

4、模板题

Code：

#include <bits/stdc++.h>
#define maxn 100010
using namespace std;
int f[maxn], key[maxn], son[maxn][2], size[maxn], q[maxn], tag[maxn], n, m, rt, sz;inline int read(){int s = 0, w = 1;char c = getchar();for (; !isdigit(c); c = getchar()) if (c == '-') w = -1;for (; isdigit(c); c = getchar()) s = (s << 1) + (s << 3) + (c ^ 48);return s * w;
}void update(int x){size[x] = 1; if (son[x][0]) size[x] += size[son[x][0]];if (son[x][1]) size[x] += size[son[x][1]];
}int get(int x){ return son[f[x]][1] == x; }void pushdown(int x){if (tag[x]){tag[x] = 0;tag[son[x][0]] ^= 1;tag[son[x][1]] ^= 1;swap(son[x][0], son[x][1]);}
}void connect(int x, int y, int z){ f[x] = y, son[y][z] = x; }void rotate(int x){int fa = f[x], ffa = f[fa], m = get(x), n = get(fa);connect(x, ffa, n);connect(son[x][m ^ 1], fa, m);connect(fa, x, m ^ 1);update(fa); update(x);
}void splay(int x, int goal){int len = 0;for (int i = x; i; i = f[i]) q[++len] = i;for (int i = len; i; --i) pushdown(q[i]);while (f[x] != goal){int fa = f[x];if (f[fa] != goal) rotate(get(x) == get(fa) ? fa : x);rotate(x);}if (!goal) rt = x;
}void insert(int x){int now = rt, fa = 0;while(now) fa = now, now = son[now][x > key[now]];now = ++sz;key[now] = x;f[now] = fa;if (fa) son[fa][x > key[fa]] = now;size[now] = 1;son[now][0] = son[now][1] = 0;splay(now, 0);
}int kth(int x){ int now = rt;while (1){ pushdown(now);if (size[son[now][0]] >= x) now = son[now][0]; else{x -= size[son[now][0]];if (x == 1) return now;--x, now = son[now][1]; }}
}void work(int l, int r){l = kth(l); r = kth(r + 2);splay(l, 0); splay(r, l);tag[son[r][0]] ^= 1;
}void write(int x){pushdown(x);if (son[x][0]) write(son[x][0]);if (key[x] > 1 && key[x] < n + 2) printf("%d ", key[x] - 1);if (son[x][1]) write(son[x][1]);
}int main(){n = read(), m = read();for (int i = 1; i <= n + 2; ++i) insert(i);while (m--){int l = read(), r = read();work(l, r);}write(rt);return 0;
}

5、结语

排版有些乱（⊙﹏⊙汗
我还在寻找自己的风格，每天文化课有些紧，上机时间也不多，题目也做的不多
不是特别熟练也请谅解

习题

[CQOI2014]排序机械臂：练手好题，加深理解
[NOI2004]郁闷的出纳员：有点思维难度
送花：裸题，你需要很快的秒了
宝石管理系统：如果短时间内完成，说明你掌握的还不错
[HNOI2004]宠物收养场：比较简单的Splay
[ZJOI2006]书架：有点烦，有点难调
[NOI2003]文本编辑器：非常基本的操作训练
[HNOI2012]永无乡：splay dsu
[NOIp2017]列队：较毒瘤，好题
序列终结者：裸题，秒杀
[HNOI2002]营业额统计：裸题++


http://chatgpt.dhexx.cn/article/wSg7a4Fi.shtml

相关文章

平衡树详解（Splay）

平衡树详解（Splay）

引入 先看例题&#xff1a;&#xff08;洛谷 P3369 【模板】普通平衡树&#xff09; 您需要写一种数据结构&#xff0c;来维护一些数&#xff0c;其中需要提供以下操作&#xff1a; 1.插入 x x x 数 2.删除 x x x 数(若有多个相同的数&#xff0c;因只删除一个) 3.查询 x x…
阅读更多...
Splay入门解析【保证让你看不懂（滑稽）】

Splay入门解析【保证让你看不懂（滑稽）】

upd&#xff1a;忽然发现直接在百度上搜索 splay s p l a y 就会搜索到我这篇文章&#xff1f;小蒟蒻瑟瑟发抖。 因为CSDN这边我基本不会看回复什么的&#xff0c;所以如果有问题还是请移步cnblogs里面吧 Cnblogs里面这篇文章的链接 BST真是神奇的东西。。。 而且种类好多呀…
阅读更多...
Splay Tree

Splay Tree

类别&#xff1a;二叉排序树 空间效率&#xff1a;O(n) 时间效率&#xff1a;O(log n)内完成插入、查找、删除操作 创造者&#xff1a;Daniel Sleator和Robert Tarjan 优点&#xff1a;每次查询会调整树的结构&#xff0c;使被查询频率高的条目更靠近树根。 注&#xff1a;所有…
阅读更多...
【算法详解】splay的初步了解

【算法详解】splay的初步了解

qwq表示最近感受到了不停课的鸭梨啊&#xff0c;好难搞啊……算法太难学了……我好菜啊qwq 其实半个多月前就可以写这篇文章&#xff0c;不过由于时间紧张没写emmmmmm&#xff0c;不扯闲言乱语了&#xff0c;如果有什么写的不好的地方凑活一下吧2333333333 splay是一种可以使树…
阅读更多...
splay详解

splay详解

一&#xff1a;什么是splay&#xff08;伸展树&#xff09; 首先了解二叉排序树 二叉排序树或者是一棵空树&#xff0c;或者是具有下列性质的 二叉树&#xff1a; &#xff08;1&#xff09;若左子树不空&#xff0c;则左子树上所有结点的值均小于或等于它的 根结点的值&#…
阅读更多...
Splay 总结基础精华

Splay 总结基础精华

前言&#xff1a; 第一次学习Splay是2月份&#xff0c;打板子的时候是3月份&#xff0c;Ac是4月份&#xff0c;写这篇博客是6月初&#xff1b;原因是因为我竟然发现我忘了Splay的板子了&#xff01;很慌&#xff0c;必须总结一下&#xff01; 不敢说是最详细的&#xff0c;但希…
阅读更多...
关系型数据库与非关系型数据库详解

关系型数据库与非关系型数据库详解

关系数据库与非关系型数据库 一、数据库概述1、关系型数据库2、非关系型数据库 二、数据库区别1、数据存储方式不同2、扩展方式不同3、对事务性的支持不同 三、非关系型数据库产生背景四、Redis简介1、Redis 优点 五、Redis 安装部署六、Redis 命令工具&#xff08;1&#xff0…
阅读更多...
关系型数据库RDS基本简介

关系型数据库RDS基本简介

OSS存放非结构化的数据&#xff0c;如&#xff1a;音频、视频、图片 rds存放结构化的数据&#xff0c;如&#xff1a;一张表&#xff0c; RDS产品概要 可以根据业务的需求进行弹性伸缩。 采用主从备份架构&#xff0c;三节点数据存储&#xff0c;具备高可用性和数据可靠性 …
阅读更多...
2 关系型数据库是什么？

2 关系型数据库是什么？

目录结构 关系型数据库基本概念结构化查询语言数据定义语言&#xff08;DDL&#xff09;数据查询语言&#xff08;Data Query Language, DQL&#xff09;数据操纵语言&#xff08;Data Manipulation Language, DML&#xff09;数据控制语言&#xff08;Data Control Language, …
阅读更多...
常见的关系型数据库有哪些

常见的关系型数据库有哪些

Oracle Database&#xff1a;由Oracle公司开发和维护的商业关系型数据库&#xff0c;具有广泛的应用场景和功能。 MySQL&#xff1a;开源关系型数据库&#xff0c;常用于Web应用程序和小型企业应用。 Microsoft SQL Server&#xff1a;由Microsoft公司开发和维护的商业关系型…
阅读更多...
Bezier曲线快速相交计算(含代码)

Bezier曲线快速相交计算(含代码)

Bezier曲线快速相交计算 背景介绍算法思路解释和分析示例参考资料 背景介绍 很多时候&#xff0c;需要计算曲线段与曲线段是否有交点。常规的思路是直接联立方程求解。不过&#xff0c;直接求方程的解这种思路通常在计算上开销较大。 针对任意曲线&#xff0c;曲线的方程阶次…
阅读更多...
js绘制贝塞尔曲线（Bézier-Curve）

js绘制贝塞尔曲线（Bézier-Curve）

贝塞尔曲线(Bzier curve)&#xff0c;又称贝兹曲线或贝济埃曲线&#xff0c;是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线&#xff0c;贝兹曲线由线段与节点组成&#xff0c;节点是可拖动的支点&#xff0c;线段像可伸缩的皮筋&#xff0c;我们…
阅读更多...
Bezier曲线与B-Spline曲线

Bezier曲线与B-Spline曲线

微分几何基础 微分集合是用微分的方法来研究曲线的局部性质&#xff0c;如曲线的弯曲程度等。 一条可以用参数表示的三维曲线是一个有界点集&#xff0c;可以写成一个带参数的、连续的、单值的数学函数&#xff1a; { x x ( t ) y y ( t ) z z ( t ) 0 ⩽ t ⩽ 1 p p ( t…
阅读更多...
初识贝塞尔（bezier）曲线

初识贝塞尔（bezier）曲线

文章目录 资料援引贝塞尔曲线的用途一阶贝塞尔&#xff08;bezier&#xff09;曲线二阶贝塞尔&#xff08;bezier&#xff09;曲线三阶贝塞尔&#xff08;bezier&#xff09;曲线高阶贝塞尔&#xff08;bezier&#xff09;曲线三阶贝塞尔曲线求插值&#xff08;Slerp&#xff0…
阅读更多...
贝塞尔曲线（Bezier Curve）原理、公式推导及matlab代码实现

贝塞尔曲线（Bezier Curve）原理、公式推导及matlab代码实现

1. 定义 贝塞尔曲线(Bezier curve)&#xff0c;又称贝兹曲线或贝济埃曲线&#xff0c;是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线&#xff0c;贝兹曲线由线段与节点组成&#xff0c;节点是可拖动的支点&#xff0c;线段像可伸缩的皮筋&#…
阅读更多...
Bezier（贝塞尔曲线通用规律算法-DEMO）

Bezier（贝塞尔曲线通用规律算法-DEMO）

之前也看过一些相关贝塞尔曲线的知识&#xff0c;但就是一直没有实践应用&#xff1b; 今天&#xff0c;听到有同事&#xff1a;程序、美术&#xff0c;在讨论相关的&#xff0c;人物的曲线路径行走的问题&#xff1b; 一些数学比较牛X的&#xff0c;说了用2阶&#xff0c;或…
阅读更多...
bezier曲线原理(简单阐述)

bezier曲线原理(简单阐述)

原理和简单推导&#xff08;以三阶为例&#xff09;&#xff1a; 设P0、P02、P2是一条抛物线上顺序三个不同的点。过P0和P2点的两切线交于P1点&#xff0c;在P02点的切线交P0P1和P2P1于P01和P11&#xff0c;则如下比例成立&#xff1a; 这是所谓抛物线的三切线定理。 当P0&…
阅读更多...
Bezier贝塞尔曲线

Bezier贝塞尔曲线

1.简介 Bezier曲线在图形学和游戏中经常使用&#xff0c;一般用的比较多的是4个控制点的贝塞尔曲线&#xff0c;这里手写了一个仅供参考&#xff08;注&#xff1a;理论上也可以写任意多个点&#xff08;3个及以上&#xff09;的贝塞尔&#xff0c;就是一个递归的过程&#xff…
阅读更多...
java 贝塞尔曲线_在Java中绘制贝塞尔曲线

java 贝塞尔曲线_在Java中绘制贝塞尔曲线

我需要创建一个简单的Java程序,通过任意数量的点逐个像素地绘制贝塞尔曲线.此刻,一切似乎都没问题,只是曲线总是在x 0 y 0坐标处结束. 截图1 截图2 我需要它在最后一点结束.我的大脑今天工作不太好,所以我正在寻求帮助. 这是我有的&#xff1a; private void drawScene(){ pr…
阅读更多...
贝塞尔曲线（Bezier Curve）原理及公式推导

贝塞尔曲线（Bezier Curve）原理及公式推导

1. 定义 贝塞尔曲线(Bezier curve)&#xff0c;又称贝兹曲线或贝济埃曲线&#xff0c;是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线&#xff0c;贝兹曲线由线段与节点组成&#xff0c;节点是可拖动的支点&#xff0c;线段像可伸缩的皮筋&#…
阅读更多...
推荐文章

Copyright @ 2022~2023