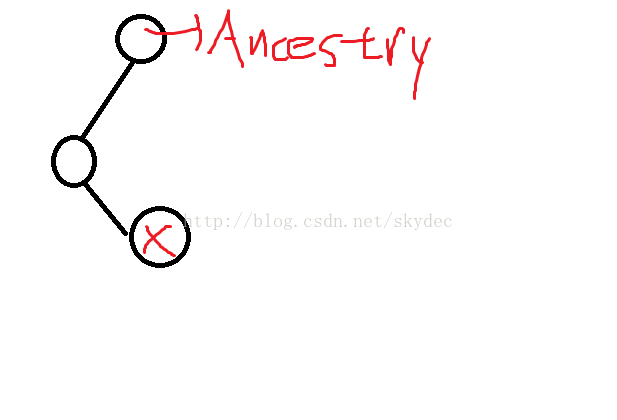首先声明,本教程的对象是完全没有接触过splay的OIer,大牛请右上角。。
PS:若代码有误,请尽快与本人联系,我会尽快改正
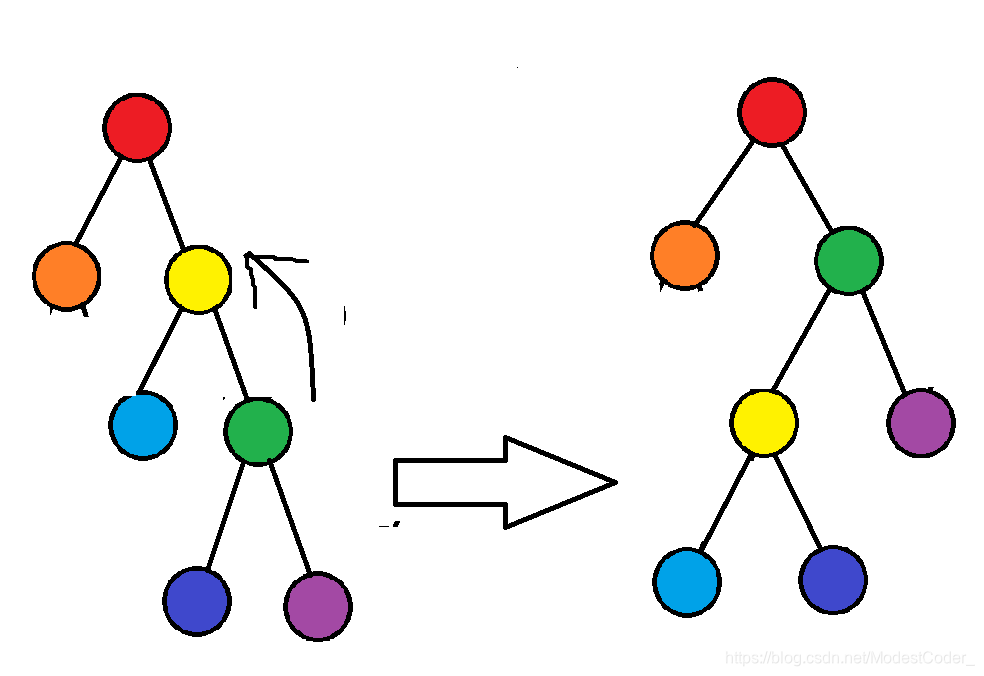
首先引入一下splay的概念,他的中文名是伸展树,意思差不多就是可以随意翻转的二叉树
PS:百度百科中伸展树读作:BoGang,不知道是不是因为和某位大牛有关系
先看一道题目:
skydec有n个数,每次他都会把一些数放进一些盒子里,由于skydec太傻×,所以他不能判断数的大小,现在他请求你帮他求盒子里的第K小数
输入:一个数n表示数的个数,一个数m表示操作的个数 (n<=m<=100000)
操作由2部分组成,简称为a和b,如果a=0,则表示将b放进盒子里,如果a=1,则表示询问盒子里的第b小数
输出:对于每次询问输出答案
由于是临时造的题目,就不造样例了,引用一句RZZ大神的话:题是死的,人是活的,出题人是懒的。
如果是普通的查询的话,只要排序一遍直接输出data[b]。但是这是动态的
这里就要引进二叉搜索树了,二叉搜索树我就不介绍了,这都不知道的话也没必要来读这篇教程了= =。对于一个节点,我们可以从根开始,一直左右子树搜寻,直到搜到一个排名为k的数,具体实现:find(node,k)表示在以node为根的树中查找第k小的树。
当k=size[leftson[node]]+1时,显然根结点就是答案
然后分类讨论,当k<size[leftson[node]]+1时,往左子树搜寻,即返回find(leftson[node],k)
当k>size[leftson[node]]时,往右子树搜寻,即返回find(rightson[node],k-1-size[leftson[node]])
至于插入过程,我就不说了,太简单了
long find(long x,long k)
{long leftsize=size[leftson[x]];if(k==leftsize+1)return x;if(k<leftsize+1) return find(leftson[x],k);else return find(rightson[x],k-leftsize-1);
}如果是随机数据的话,这题随便无压力过,但是skydec开始丧心病狂了,他插入的数是递减的,这样的话这种方法就会导致时间复杂度O(n^2)
那么现在就要引进传说中的splay树了!
splay树是通过不断的旋转来维持logn的平均复杂度的,他不用像AVL树严格平衡,也不用记录高度等平衡信息,是十分灵活的,唯一的缺点就是常数比其他平衡树要大一点
但是我初学时一直有一个疑问:splay是如何维持logn的复杂度的呢
由于splay是不断翻转的,所以就算某一时刻他成了一条链,也会马上变成另外的形态,通过这样不断地变换可以防止长期停留在链的状态
打个比方,如果你有100元,你可以在某个彩票上孤注一掷,也可以买50张彩票,由于孤注一掷可能会跪掉,所以肯定是买50张好,因为就算跪了,也不会赔太多钱
然后平均时间就是logn了
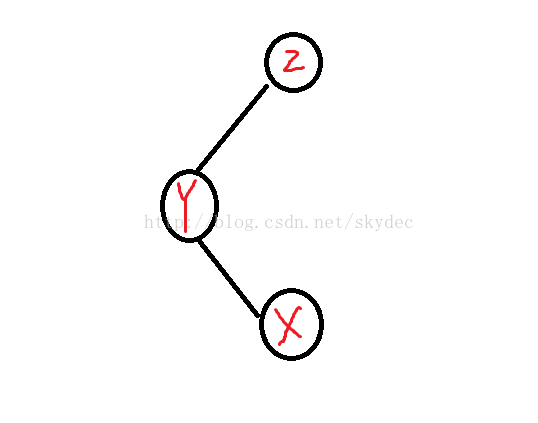
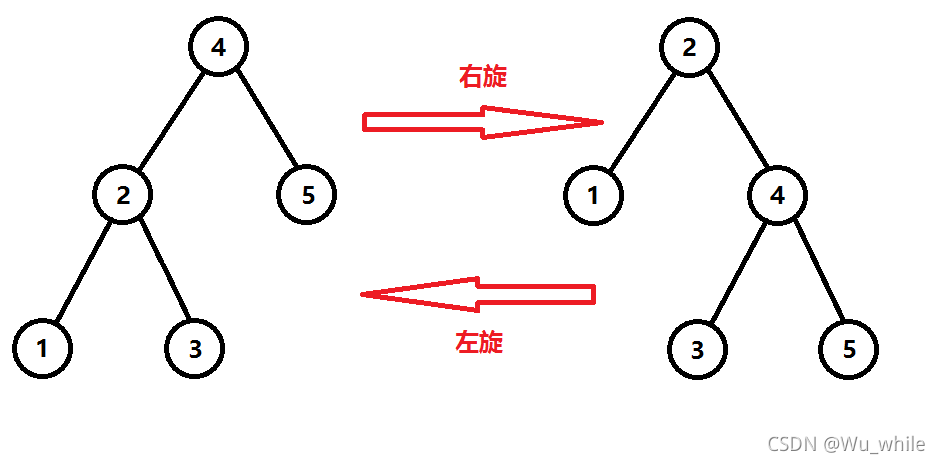
现在引入旋转这个概念
其中,我们是以X结点为主角的
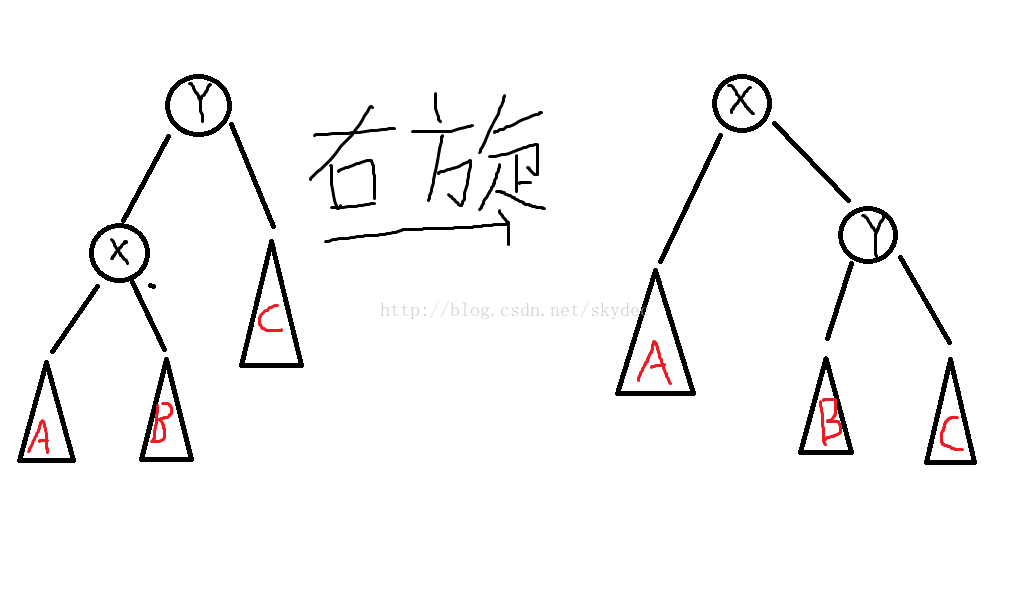
现在来解释一下这一幅图
解释之前,肯定有人要问了:这旋转有个鸟用。其实这次旋转成功地将结点X上提了一步,其实splay的最终目标就是把某个结点提到他的某个祖先的下面。
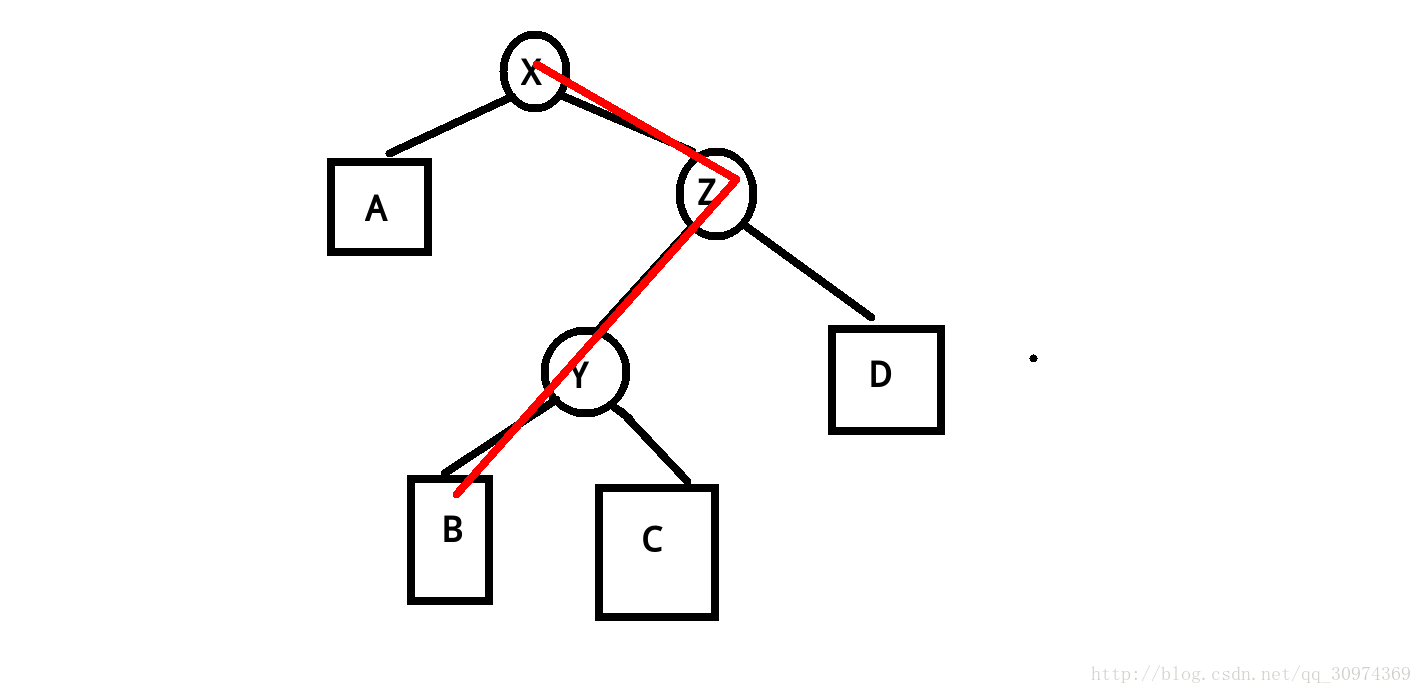
右旋其实只需要三步:
1.将X的右子树B(如果有的话)作为Y的左子树,同时让B认Y作爹
2.设Z为原本Y结点的父亲,让X认Z做爹(如果Z存在的话),将X作为Z的儿子(是左是右得由Y是Z的左儿子还是右儿子决定,要左右一致)
3.将Y作为X的右子树,同时让Y认X作爹
下面贴个代码吧,希望看得懂
void right_rotate(long x)
{long y=father[x];long z=father[y];leftson[y]=rightson[x];if(rightson[x]!=0)father[rightson[x]]=y;//对图中B子树,即X的右子树的处理father[x]=z;if(z!=0){if(leftson[z]==y)leftson[z]=x;else rightson[z]=x;}rightson[x]=y;father[y]=x;
}
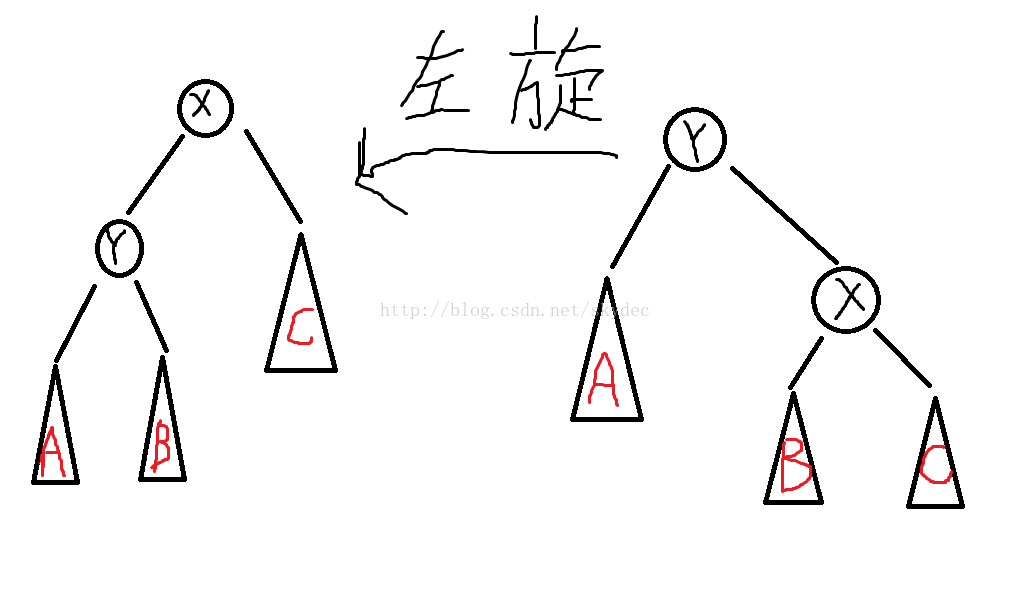
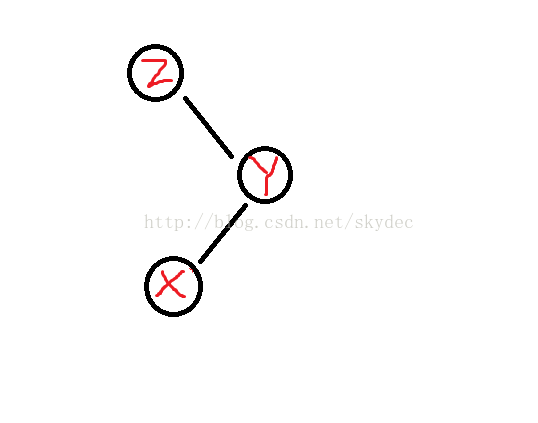
左旋同理,为了节省时间,就不多解释了,直接贴代码吧
void left_rotate(long x)
{long y=father[x];long z=father[y];rightson[y]=leftson[x];if(leftson[x]!=0)father[leftson[x]]=y;father[x]=z;if(z!=0){if(leftson[z]==y)leftson[z]=x;else rightson[z]=x;}leftson[x]=y;father[y]=x;
}下面来一个合集
O(∩_∩)O~请允许我写一个装13的代码
void rotate(long x,int kind)
//kind=0表示左旋,kind=1表示右旋 ch[X][0..1]表示X的左儿子和右儿子
{long y=father[x];long z=father[y];ch[y][!kind]=ch[x][kind];if(!ch[x][kind])father[ch[x][kind]]=y;father[x]=z;if(!z)ch[z][ch[z][1]==y]=x;father[y]=x;ch[x][kind]=y;
} 开始splay树最最最最最核心的操作----------splay
splay(x,Ancestry)表示将x不停向上旋转,知道X成为结点Ancestry的子树 (Ancestry意为祖先,装13专用)
一般应用比较广泛的是将X结点Splay到根节点
下面放一下伪代码
void splay(long x,long Ancestry)
{while(father[x]!=Ancestry){各种旋转(~ o ~)~zZ}
} 众人:(啪!)你特么不是写了跟没写一样么
好吧,下面开始补全各种旋转
旋转分为2种情况,其中两种情况又总共分为6种情况
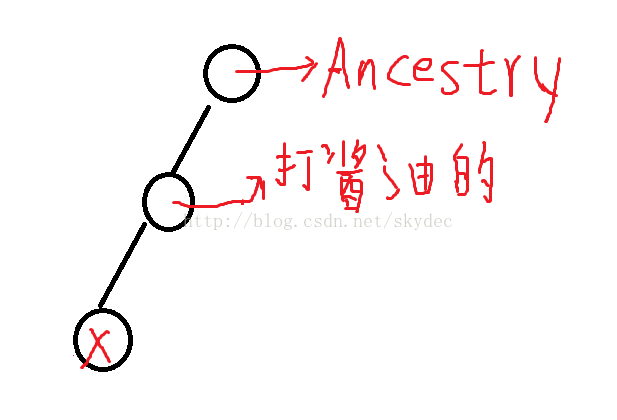
第一种情况,Ancestry是X的父亲的父亲(可以称作爷爷了。。)
然后又分为两种情况:
1.
其中有些结点我懒得话了,比如X的右兄弟
这种情况下,只需要执行一遍 right_rotate(x)即可
2.
这种情况下,只需要执行一遍left_rotate(x)
//-------------------------------------------------------------------------------------------------------------------------------//
以上两种都是Ancestry是X的爷爷的情况
下面两种是Ancestry还不是X的爷爷的情况
3.
当leftson[z]=y且rightson[y]=x时,只需要执行两部:left_rotate(x), right_rotate(x)
4.
当rightson[z]=y且leftson[y]=x时,只需要:right_rotate(x),left_rotate(x)即可
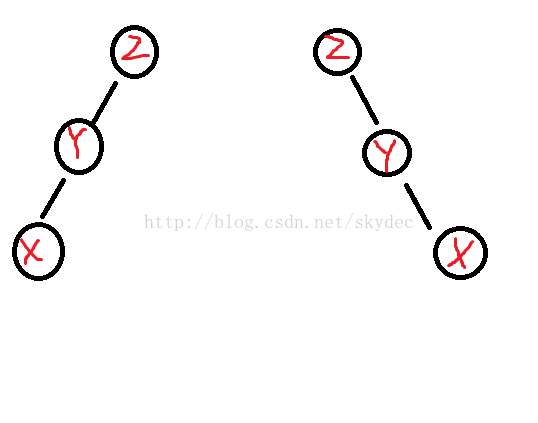
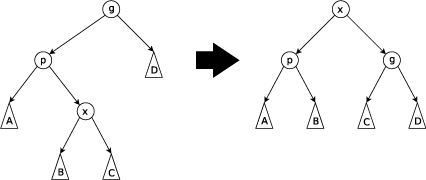
五六两种情况合起来讨论:
当形成类似一条线时
左边的情况:right_rotate(y),right_rotate(x);
右边的情况:left_rotate(y);left_rotate(x);
至于为什么要先旋转Y结点,我也不知道
那么到此为止,6种旋转都介绍完了,下面贴一波代码
void splay(long x,long Ancestry)
{while(father[x]!=Ancestry){long y=father[x];long z=father[y];if(z==Ancestry){if(rightson[y]==x)left_rotate(x);else right_rotate(x);}else{if(rightson[z]==y&&rightson[y]==x){left_rotate(y);left_rotate(x);}else if(rightson[z]==y&&leftson[y]==x) {right_rotate(x);left_rotate(x);}else if(leftson[z]==y&&leftson[y]==x) {right_rotate(y);right_rotate(x);}else {left_rotate(x);right_rotate(x);}}}if(Ancestry==0)root=x;
} 然后下面来一个装13版
void splay(long x,long Ancestry)
{while(father[x]!=Ancestry){long y=father[x];long z=father[y];if(z==Anc