昨天这个时候到现在终于把Splay给搞明白了，还A了一道郁闷的出纳员；刚学完的感受：我再也不碰这东西了；做完郁闷的出纳员的感受：我发誓这辈子不当出纳员(虽然这确实只是个入门题……)
于是来讲一讲这个恶心的东西吧……(全程不用指针，请做好心理准备……)
学习前请先学习下二叉搜索树，里面可能直接用到这个东西
首先，Splay是一个数据结构，为了突出它是一个数据结构，所以给他开个结构体……

struct tree
{int val,sz,cnt;//val为值 sz为子树大小，cnt为"有多少这个值"//cnt:假如出现了两个一模一样的值，只需要让cnt+1就可以了，cnt是数目int s[2],f;//s[0]为左儿子 s[1]为右儿子 f为父亲
};

为了之后的操作，我们再写三个函数(如果认为没用可以先跳过，过一会用到了再回来看)

bool son(int x) //返回x是左儿子还是右儿子，如果为左儿子，返回0，右儿子则返回1
{return a[a[x].f].s[1] == x;
}void rejs(int x)    //重新计算以x为根，子树的大小，子树大小等于左子树大小加右子树大小(好吧我承认我英语拙计)
{a[x].sz = a[a[x].s[0]].sz + a[a[x].s[1]].sz + a[x].cnt;
}void point(int x,int y,bool z)  //在x下面插入y，y是x的z儿子(z为0则左儿子，z为1为右儿子)
{a[x].s[z] = y;a[y].f = x;
}

写完这几个树的基本函数，我们要开始讲splay啦(似乎我之前好像真的没有开始讲splay)
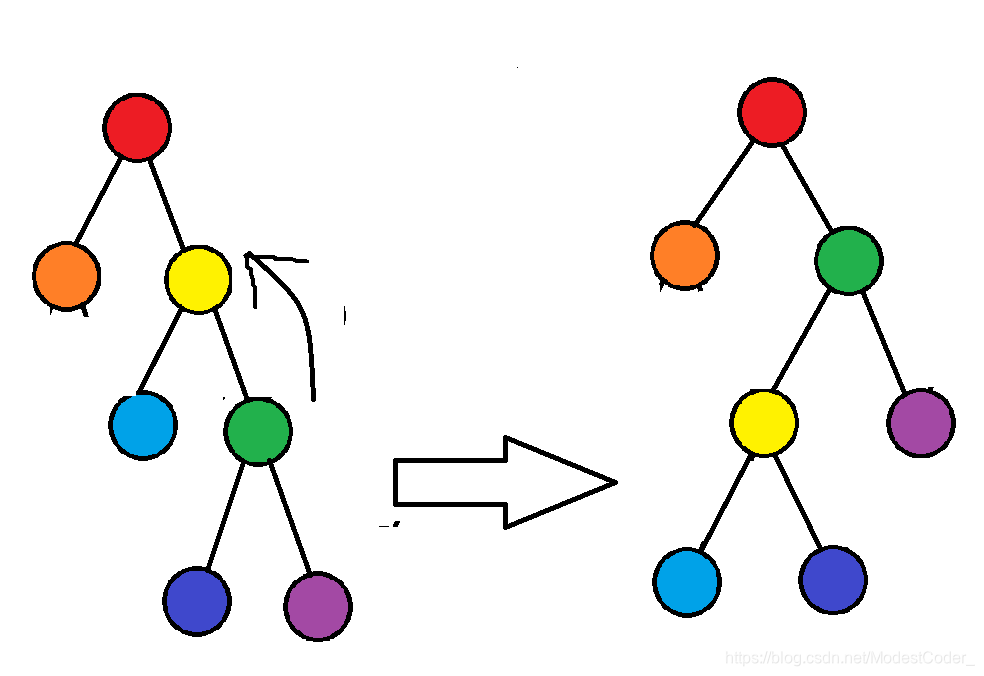
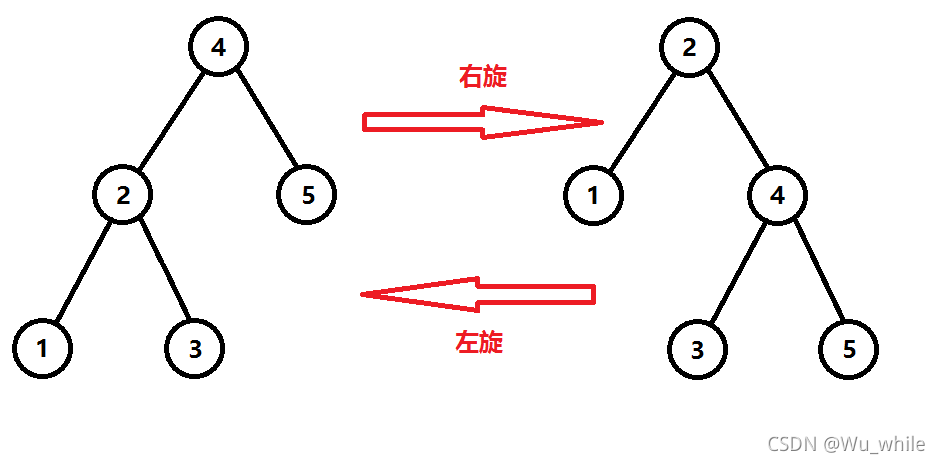
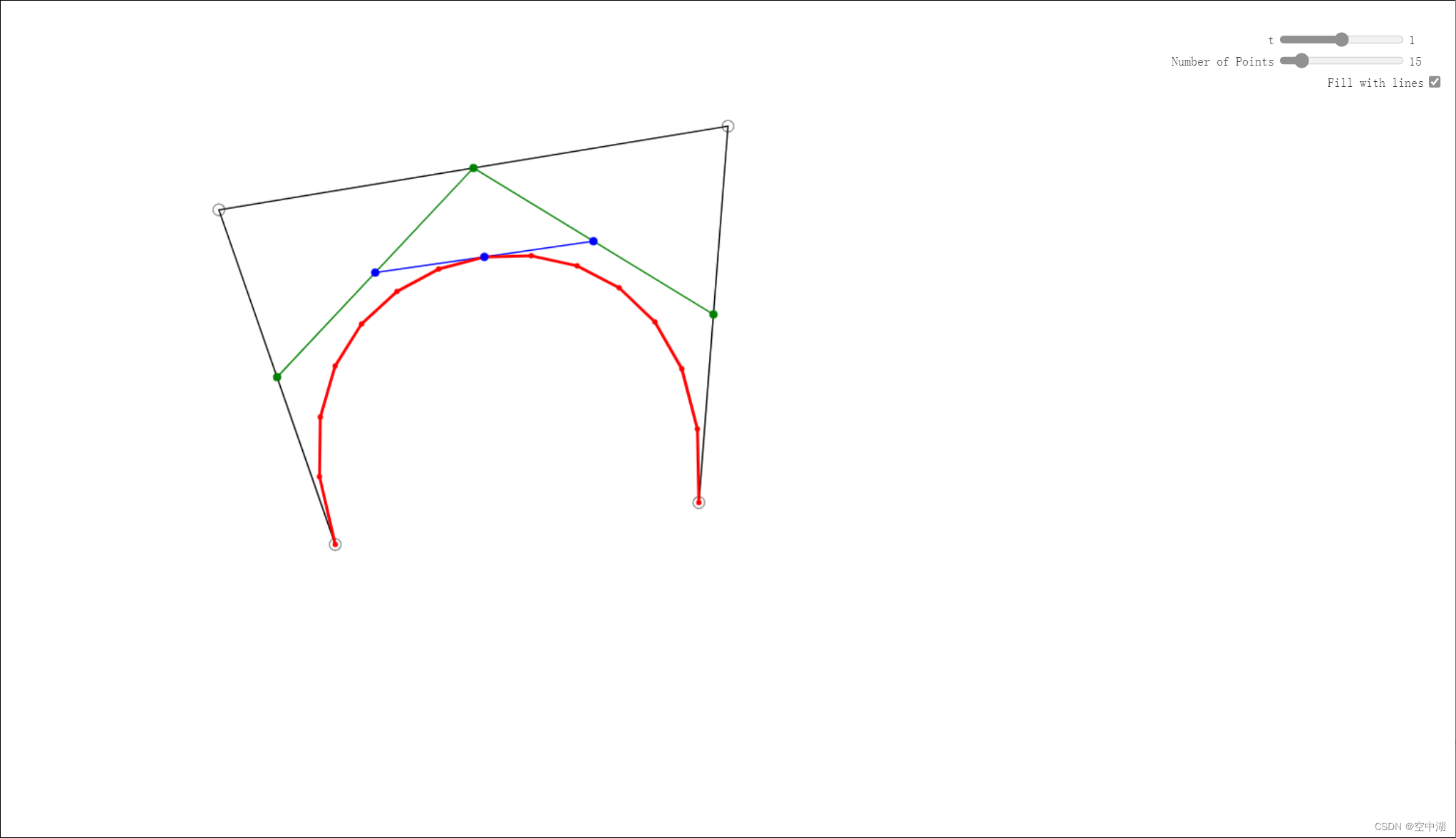
Splay最重要的一个操作就是旋转(rotate)，如下，(图片为1600x900，可直接作为桌面)：

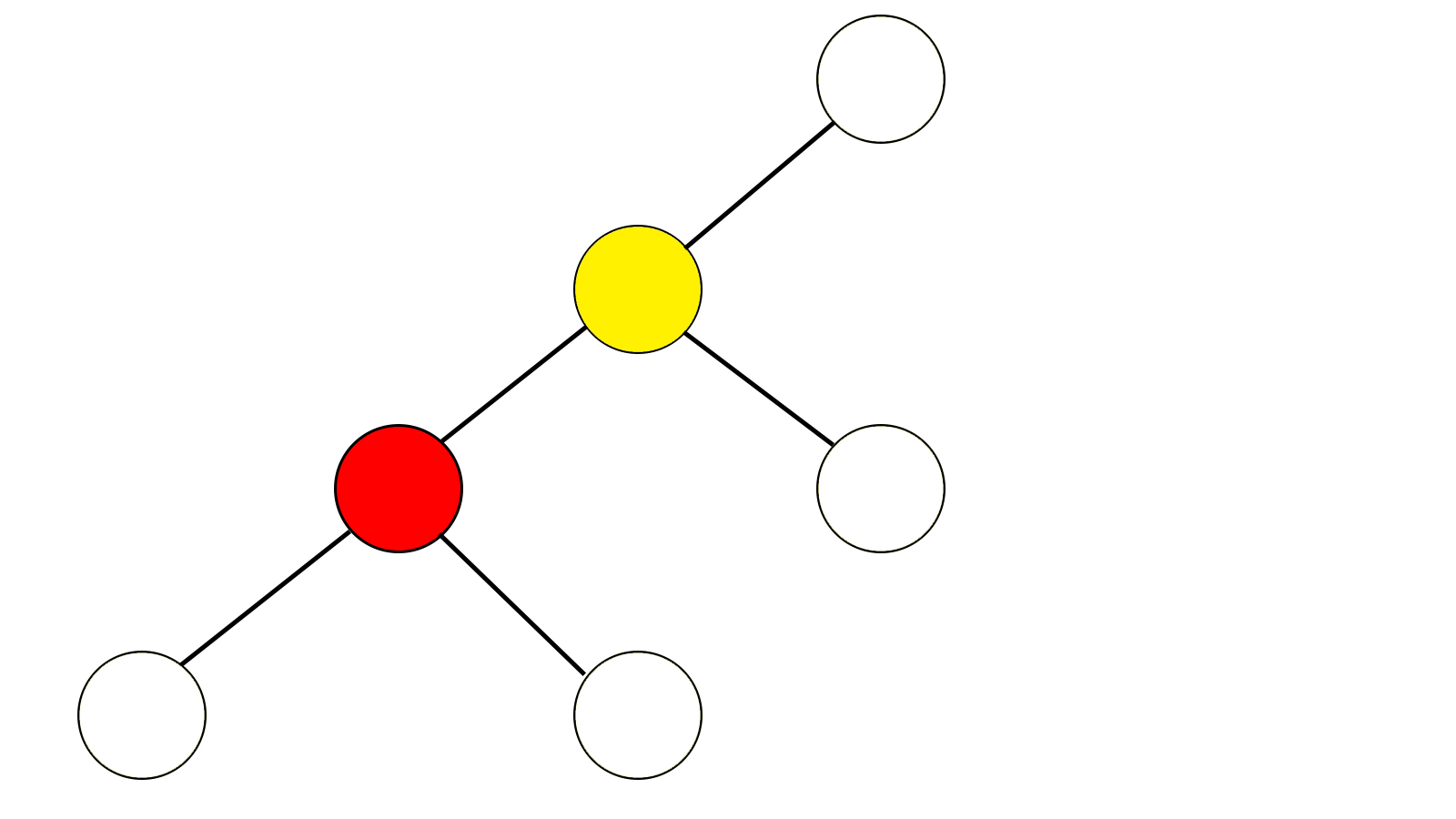
我们的目的是将红色节点旋转到它父亲的位置，即黄色节点的位置
我们应当怎么办呢？不要急，看组图

bool型变量son(黄)代表黄色节点是左儿子还是右儿子
将红色节点接到黄色节点的父亲(也就是绿色节点)的下面，是绿色节点的son(黄)儿子，也就是说代替了黄色节点；
黄色节点被代替了怎么办？再开个变量记录一下即可

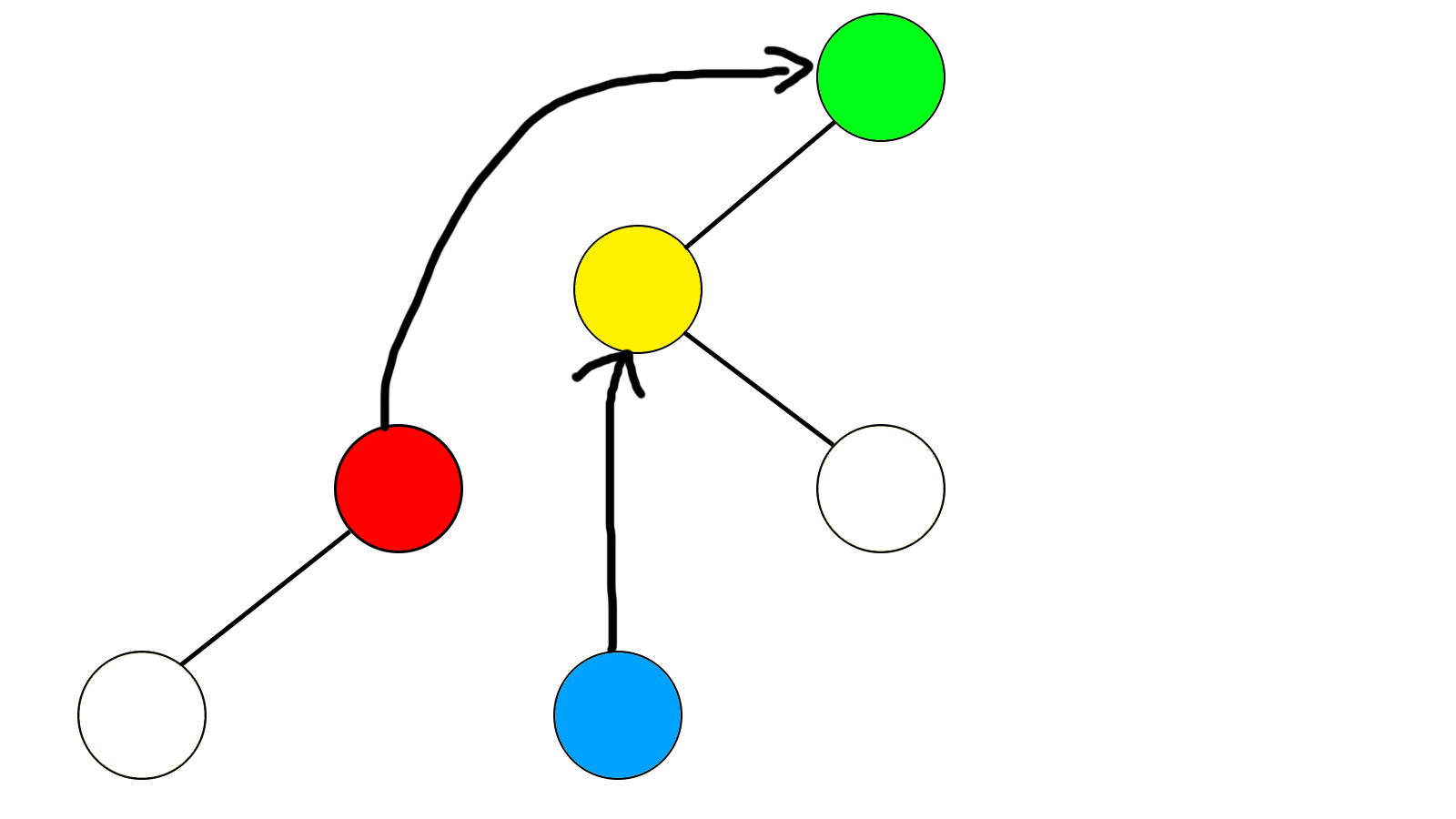
bool型变量son(红)代表红色节点是左儿子还是右儿子
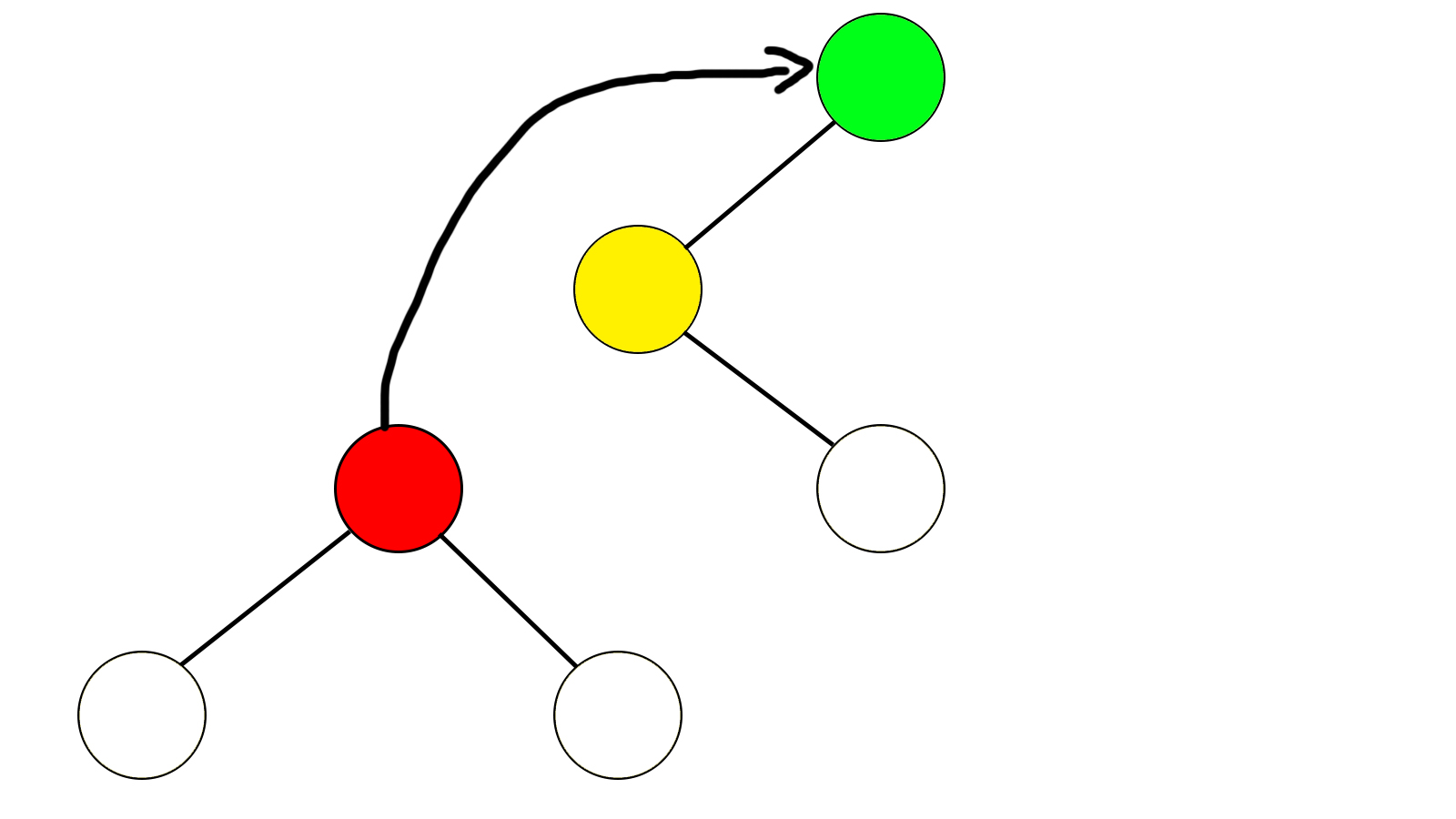
把红色节点的son(红)&1儿子(图中的蓝色节点，蓝色节点和父亲关系和红色节点和父亲关系正好相反)接到黄色节点下面，是黄色节点是son(红)儿子，代替了红色节点；

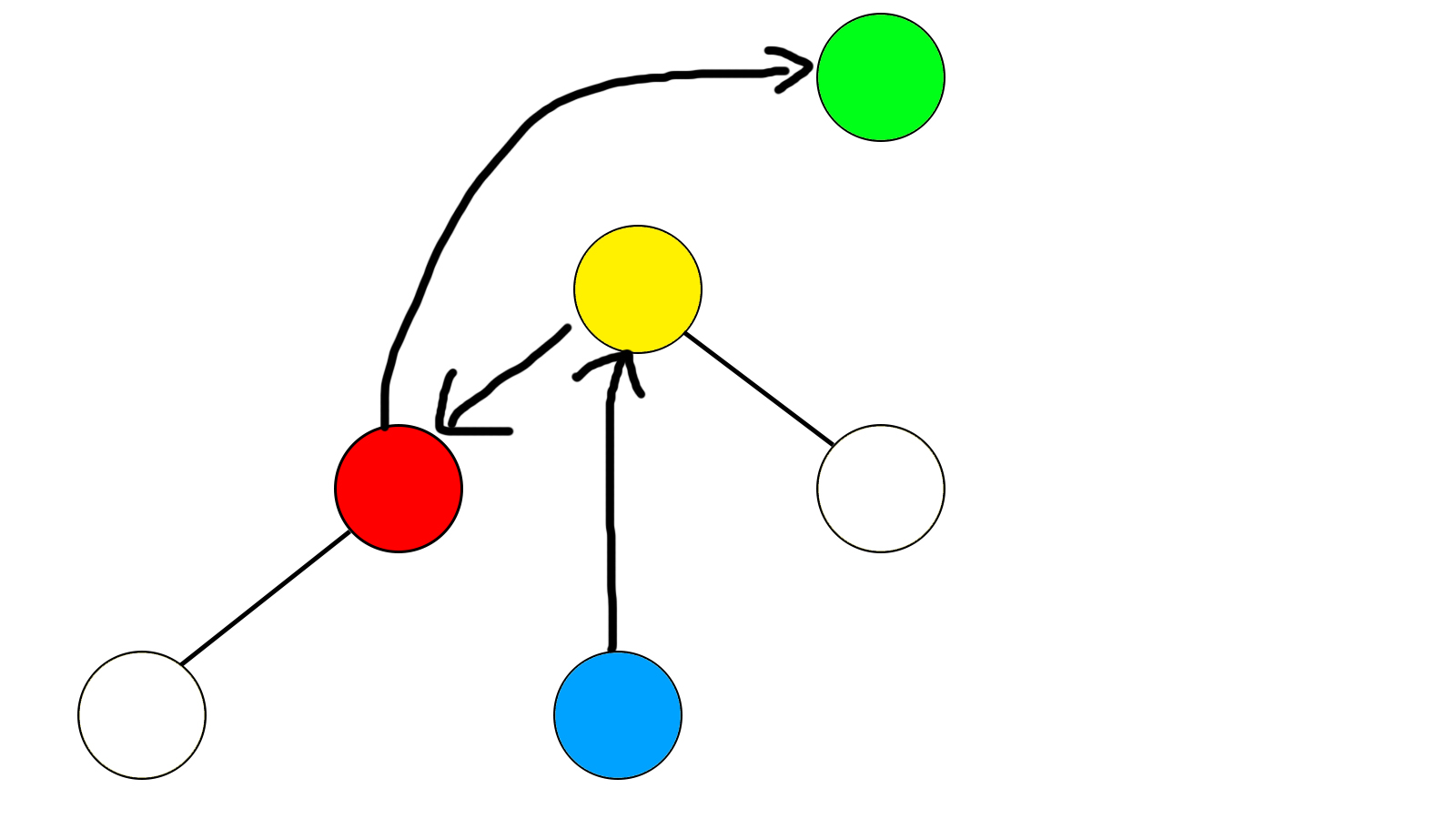
最后把黄色节点的父亲改为红色节点，旋转完成！
旋转完成后：

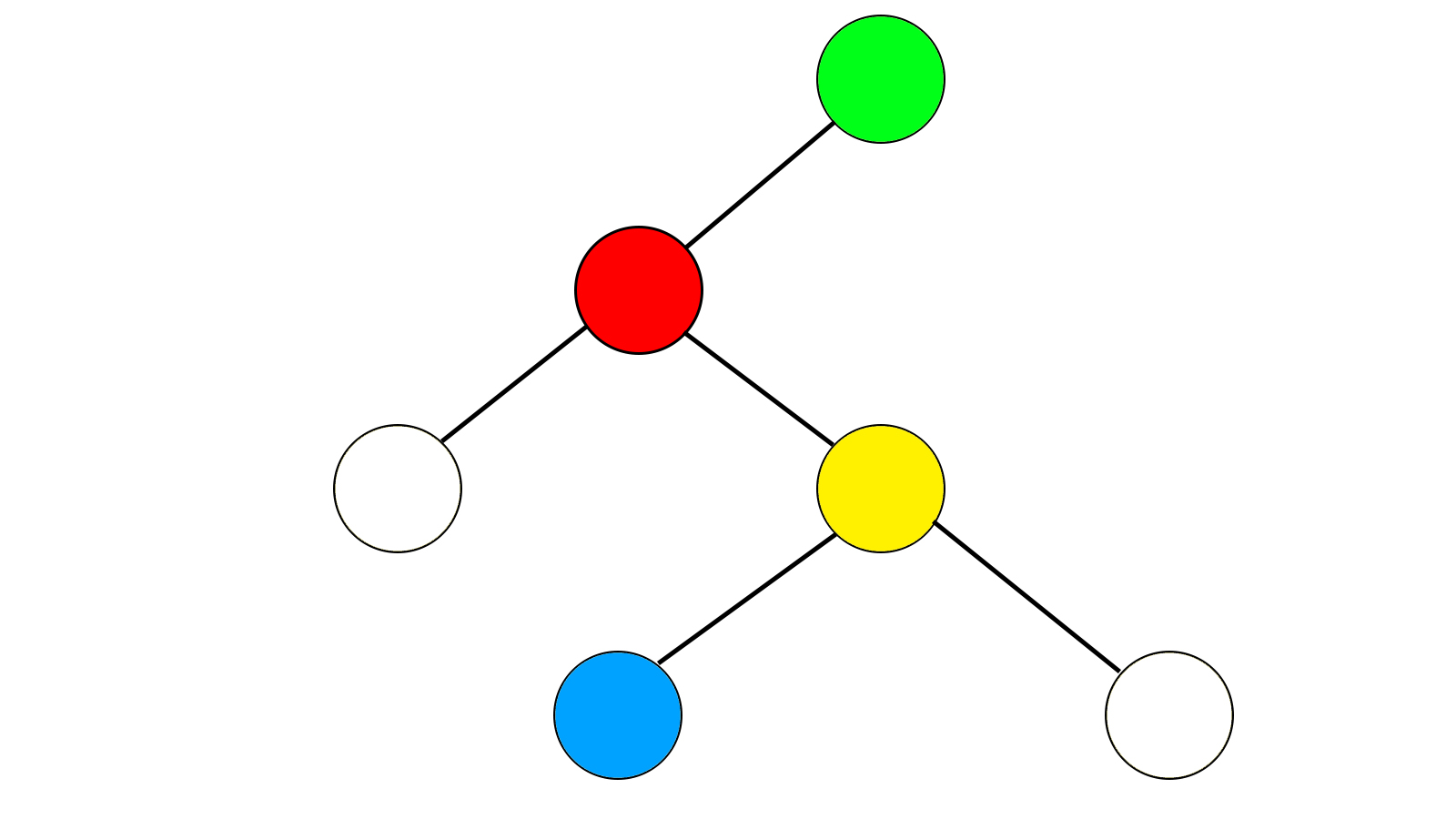
(我再也不用PS画这玩意了……)

void rot(int x)
{int p = a[x].f;bool d = son(x);point(a[p].f,x,son(p));point(p,a[x].s[d^1],d);point(x,p,d^1);rejs(p);rejs(x);if(a[x].f == 0)root = x;//root是根节点的编号
}

这就是Splay的核心操作——rotate，它的时间复杂度是——O(1)
然而学会了有什么用呢= =，下面来讲Splay的其他操作及如何平衡
首先是Splay的插入操作，Splay每插入一个新节点，就把这个节点强制旋转到根节点，如何强制旋转到根节点呢？如果while(不是根节点)rotate(x)的话就有可能退化成一条链……于是Splay“贴心”的为我们准备了splay操作……
splay操作的目的是将一个点旋转到根节点，这个操作是这样的：
1.如果这个点是根节点，那么你可以直接退出了……
2.如果这个点的父亲是根节点，那么就直接把这个点rotate上去……
3.如果上述两条均不满足，那么分类讨论：
(1)设son(x)为这个和父亲节点的关系，son(f)为父亲节点和爷爷节点的关系
(2)如果两个关系相同(均为左儿子或均为右儿子)，那么就先rotate父亲节点，然后rotate这个节点
(3)如果两个关系不同(一个是左儿子一个是右儿子)，那么就把这个节点连续rotate两次

void splay(int x)
{while(a[x].f != 0){if(a[a[x].f].f == 0)rot(x);else{if(son(x) == son(a[x].f)){rot(a[x].f);rot(x);}else{rot(x);rot(x);}}}
}

这样就可以写出插入操作了，还记得插入操作怎么做吗？插入一个节点然后splay到根节点

void ins(int x)
{int w = root,f = 0;int p = findn(x);if(p)//如果这个值已经存在，那么就直接给这个节点+1吧{a[p].cnt ++;while(p != root){rejs(p);p = a[p].f;}rejs(root);return ;}while(w){f = w;if(x < a[w].val)w = a[w].s[0];elsew = a[w].s[1];}//这是前半部分，和普通的二叉查找树插入方法一样，我承认我打的很丑……a[++tot].val = x;a[tot].cnt = 1;//新建节点，标号为totif(f == 0)//如果这个点是根节点的话，直接插入即可……{root = tot;rejs(root);return ;}//否则插入这个节点并spaly到根节点if(x < a[f].val)point(f,tot,0);elsepoint(f,tot,1);splay(tot);
}

然后是删除操作，Splay的删除操作比较丧病，我只讲一下我的写法吧……
设要删除的节点为x，那么，首先splay一下x的前驱，然后splay一下x的后继，啥？你前驱和后继还不会写？？？好吧好吧，我讲……
x的前驱是指小于x且最大的节点，后继就是大于x且最小的节点
前驱就是在x的左子树上一直往右跑，如果没有左子树那就往上找
后继就是在x的右子树上一直往左跑，如果没有右子树那也往上找
自行yy可解

int near(int x,bool d)
{if(a[x].s[d] != 0){int p = a[x].s[d];while(a[p].s[d^1])p = a[p].s[d^1];return p;}else if(son(x) == d^1)return a[x].f;else{int p = a[x].f;while(son(p) == d){if(p == root)return 0;p = a[p].f;}return a[p].f;}
}

接着继续我们的删除操作，删除操作就是上面讲的：splay(x的前驱)，splay(x的后继)，然后x的后继变为根节点，x的前驱变为根节点的左儿子，x到哪里了呢？
x成为了x前驱的右子树！直接砍掉这个右子树就ok啦~(如果删除区间也可以这样做，splay区间左边界的前驱，splay区间右边界的后继，整个区间就变成了区间左界前驱的右子树~(≧▽≦)/~)

void cle(int x)//cle操作是清除一个点，没有也无所谓吧
{a[a[x].f].s[son(x)] = 0;a[x].val = 0;a[x].sz = 0;rejs(a[x].f);a[x].f = 0;
}void del(int x)
{int p = near(x,0);int q = near(x,1);if(!p || !q){splay(x);if(p == 0){root = a[x].s[1];a[a[x].s[0]].f = 0;}else{root = a[x].s[0];a[a[x].s[0]].f = 0;}return ;}splay(p);splay(q);rot(p);cle(x);
}

至此你终于获得了一棵可用的splay，拿去乱搞吧！