Splay入门详解

写在前面

听说平衡树是一种强大的数据结构，听同年级或高年级大佬们讲起来也感觉很牛笔的亚子，而最近XC又叫我们去学习一下$LCT$！？
又因为$Splay$是学习$LCT$的基础，而且又比较脍炙人口，于是我便学了一下，经过一个白天的努力，也终于是学会了一点皮毛。
为了加深我对$Splay$的理解，把网上一些讲得有点模糊的知识点给没看懂的同学讲解清楚，于是我就写了这篇博客，保证大家都可以入门 （不行也别怪我哦）

Splay是神马东东？

给出百度的解释：$Splay$
下面我用简单易懂的语言来简单介绍一下：
首先$Splay$是一棵二叉查找树，之后$Splay$又可以通过各种骚操作（主要是旋转操作）使得整棵树仍然满足二叉查找树的性质，并且保持相对的平衡，不至于退化成链而大大提高复杂度，这个神奇的东西是由Daniel Sleator 和 Robert Tarjan这两位大神发明的
那二叉查找树又是神马呢？
首先他肯定是一棵二叉树 （废话）
而且这棵树有一个非常厉害的性质：能够在这棵树上查询到的节点一定满足：左子树任意节点的值$<$根节点的值$<$右子树任意节点的值

例题 LOJ #104.普通平衡树

这道题的题目大意就是有n个操作，一共有6种操作，对应1~6编号：
1.插入$x$数
2.删除$x$数(若有多个相同的数，因只删除一个)
3.查询$x$数的排名(排名定义为比当前数小的数的个数+1)
4.查询排名为$x$的数
5.求$x$的前驱(前驱定义为小于 $x$，且最大的数)
6.求$x$的后继(后继定义为大于 $x$，且最小的数)
之后对于3,4,5或6操作的结果进行输出

详解Splay操作

接下来我们来结合我的解析和代码对Splay的操作进行了解

变量

int n;//操作个数
int son[N][2];//该节点的左/右儿子的编号，0表示左儿子，1表示右儿子
int fa[N];//该父亲节点
int cnt;//节点的总数
int tot[N];//该节点权值出现的次数
int size[N];//以该节点为根的子树大小
int root;//根节点
int val[N];//该节点的权值

三个最基本的操作

• 改变节点在树中的位置之后，更新该节点的$size$值：$maintain(x)$

inline void maintain(int x) {size[x]=size[son[x][0]]+size[son[x][1]]+tot[x];}
//左子树的大小加上右子树的大小在加上该节点的值的个数

• 判断该节点是父亲的左儿子还是右儿子：$get(x)$

inline bool get(int x) {return x==son[fa[x]][1];}
//如果跟右儿子相等则返回1，否则返回0

• 销毁该节点：$clear(x)$

inline void clear(int x) {size[x]=fa[x]=son[x][0]=son[x][1]=tot[x]=val[x]=0;}
//该节点的所有数据全部清除

旋转操作 rotate(x)

这个操作是为了使$Splay$保持平衡而产生的，其本质是将某个节点上移一个位置
旋转操作需要保证：

• 整棵$Splay$ 中序遍历（就是先遍历左儿子，再遍历根节点，最后遍历右儿子） 的顺序不变（为了不破坏二叉查找树的性质）
• 旋转后受到影响的节点所维护的信息仍然是正确有序的
• $root$必须变成旋转过后的根节点

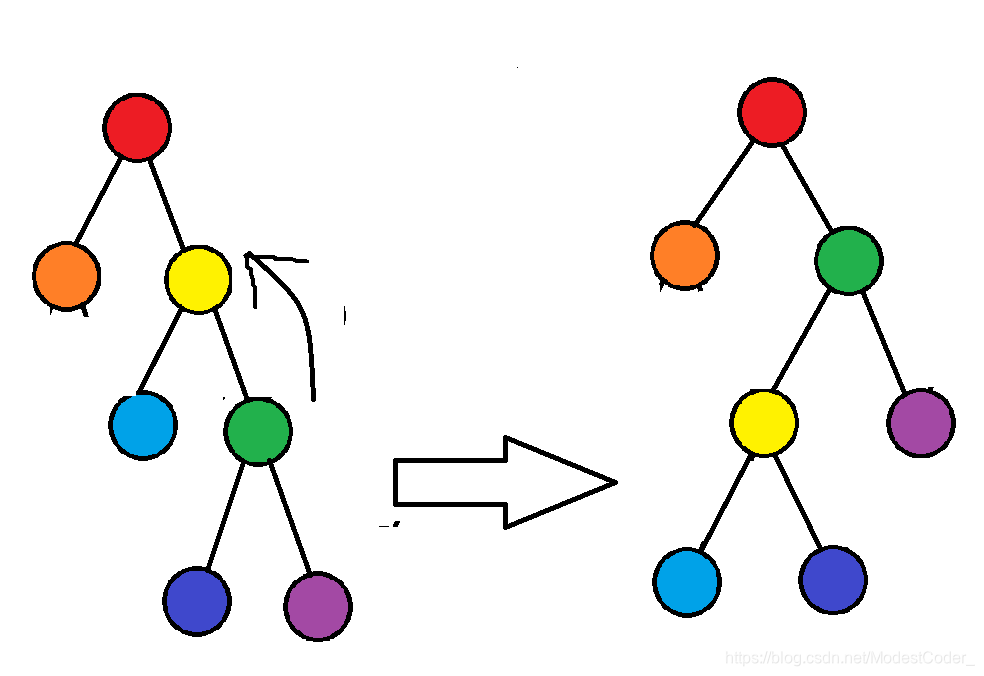
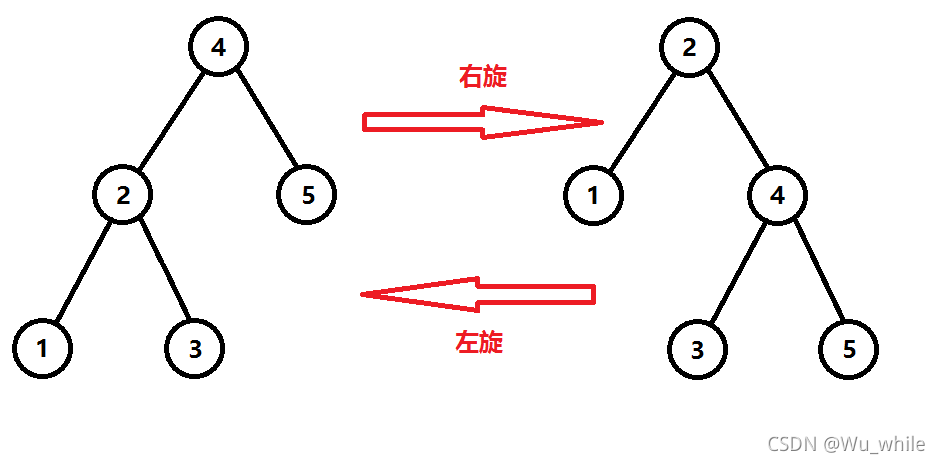
$Splay$中的旋转分为左旋和右旋两种，如图所示：

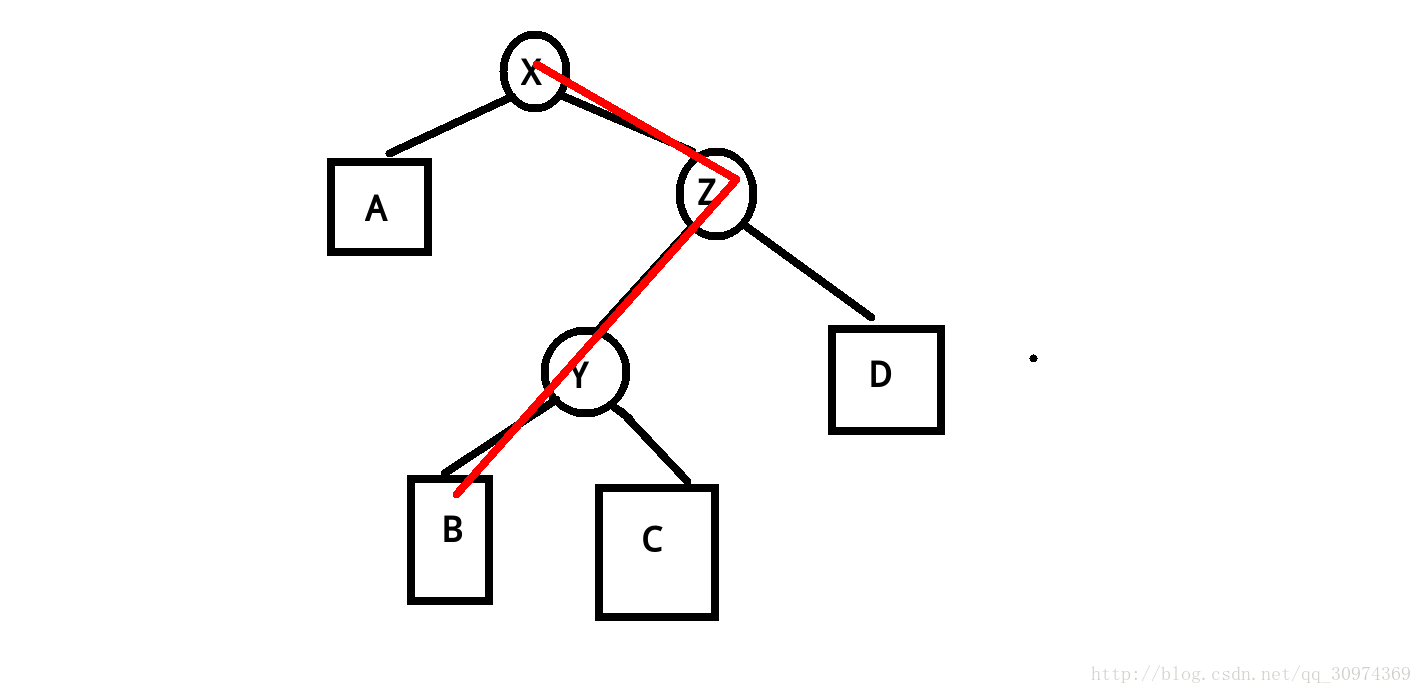
我们来分析一下旋转具体操作（这里以右旋为例子，假设需要旋转的节点为$x$，其父亲为$y$，如果是左旋则所有方向相反）：

1. 将$x$的右儿子交给$y$当它的左儿子，将$x$的右儿子的父亲赋值为$y$
2. 将$y$赋值为$x$的右儿子，将$y$的父亲赋值为$x$
3. 如果$y$存在父亲$z$，那么把$y$原来所在的$z$的儿子的位置，赋值为$x$，将$x$的父亲赋值为$z$

我们可以看到这棵$Splay$左旋右旋怎么旋它的中序遍历顺序还是：42513
通过分析我们可以发现，如果$x$是左儿子则右旋，如果是右儿子则左旋，于是我们可以先处理出一个参数k表示$x$是左儿子还是右儿子，在运用位运算异或来进行旋转

inline void rotate(int x)
{int y=fa[x],z=fa[y],k=get(x);//y是x的父亲，z是y的父亲，k表示x是左儿子还是右儿子son[y][k]=son[x][k^1];fa[son[x][k^1]]=y;//步骤1son[x][k^1]=y;fa[y]=x;//步骤2fa[x]=z;if (z) son[z][son[z][1]==y]=x;//步骤3maintain(x);maintain(y);//不要忘记了更新size值哦
}

Splay操作（重中之重）Splay(x)

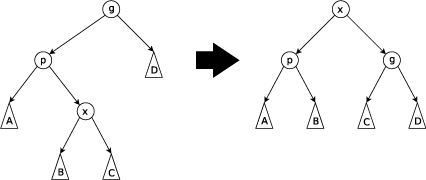
此操作是$Splay$中最特别又是最重要的操作，因为$Splay$规定了：每访问一个节点后都要强制将其旋转到根节点，而此旋转操作分以下六种情况（假设$x$是需要旋转到根节点的节点），如图所示：

• 如果$x$的父亲是根节点（如图1,2），则直接将$x$左旋或右旋即可
• 如果$x$的父亲不是根节点（如图3,4），且$x$与父亲的类型相同（同为左儿子或右儿子），则先将其父亲左旋或右旋，再将$x$右旋或左旋
• 如果$x$的父亲不是根节点（如图5,6），且且$x$与父亲的类型不同，则将$x$左旋再右旋，或右旋再左旋

inline void splay(int x)
{int y=fa[x];//先找到x节点的父亲ywhile (y)//如果x不是根节点（即x的父亲不为0）{if (fa[y])//如果x的父亲不是根节点{if (get(x)==get(y)) rotate(y);//如果x与父亲的类型相同，则旋转父亲节点else rotate(x);//否则旋转x}rotate(x);//旋转xy=fa[x];//更新父亲节点}root=x;//更新根节点
}

大家最好自己画图模拟一下以上6种情况，以充分掌握$Splay$操作，因为这个操作真的非常重要

插入操作

此操作是一个代码比较长比较复杂的操作，假设我们需要将数$k$插入$Splay$中，具体操作如下：

• 如果此时树是空树，那么直接插入根节点退出即可
• 如果当前节点的权值等于$k$，那么就增加该节点的大小，更新当前节点的$size$值和父亲节点的$size$值，之后将该节点$Slpay$操作旋转到根
• 否则就按照二叉查找树的性质往下找，找到空节点直接插入，之后将该节点 $Splay$操作旋转到根

inline void ins(int k)
{if (!root)//如果是空树（即整棵树没有根）{val[++cnt]=k;++tot[cnt];root=cnt;//直接插入到根节点maintain(root);return;//更新size值后退出}int x=root,y=0;//否则从根节点往下寻找，y表示当前节点x的父亲while (1){if (val[x]==k)//如果当前节点的权值等于k{++tot[x];maintain(x);maintain(y);//更新权值数量，更新当前节点和父亲节点的size值splay(x);break;//Splay到根然后退出}y=x;x=son[x][val[x]<k];//继续往下找if (!x)//找到一个空节点{val[++cnt]=k;++tot[cnt];fa[cnt]=y;son[y][val[y]<k]=cnt;//直接插入maintain(cnt);maintain(y);//更新当前节点和父亲的size值splay(cnt);break;//Splay到根然后退出}}
}

查询排名（以从小到大排名为例）rk(k)

假设我们需要查询数$k$在Splay中的排名，我们可以根据二叉查找树的性质使用如下操作进行查询：

• 如果$k$比当前节点的权值小，则向其左子树查找
• 如果$k$比当前节点的权值大，则将答案加上左子树的大小和当前节点的权值数量，往右子树查找
• 如果$k$等于当前节点的权值，则将答案加一然后返回即可
• 最后不要忘记将查询到等于$k$的权值的节点$Splay$到根

inline int rk(int k)
{int res=0,x=root;//从根节点开始查找while (1){if (k<val[x]) x=son[x][0];//如果k小于当前节点的权值，则往左子树查找else{res+=size[son[x][0]];//否则答案加上左子树的大小if (k==val[x]) {splay(x);return res+1;}//如果当前节点的权值等于k，则Splay到根后答案加一返回res+=tot[x];x=son[x][1];//否则即是比k小，则答案加上当前节点权值个数往右子树查询}}
}

区间第k小/大（这里以区间第k小为例）kth(k)

假设$k$为当前剩余排名，我们同样可以根据二叉查找树的性质进行查找，操作如下：

• 如果左子树不为空树且左子树大小大于等于$k$，则往左子树进行查找
• 否则将$k$减去左子树和根节点的大小。如果k小于等于0，则返回根节点的权值，否则往右子树继续查找

inline int kth(int k)
{int x=root;//从根节点开始查找while (1){if (son[x][0] && k<=size[son[x][0]]) x=son[x][0];//如果左子树不为空树且左子树大小大于等于k，则往左子树进行查找else{k-=size[son[x][0]]+tot[x];//否则将k减去左子树和根节点的大小if (k<=0) {splay(x);return val[x];}//如果k小于等于0，则Splay到根后返回根节点的权值x=son[x][1];//否则往右子树继续查找}}
}

查询k的前驱 pre()

$k$的前驱是小于$k$中的所有数最大的那个，操作很简单：
先把$k$插入进$Splay$中（此时$k$已经被$Splay$到根节点了），然后前驱即为左子树中最大的那个数，即左子树中最靠右的节点，再删除$k$

inline int pre()
{int x=son[root][0];//先查找到左子树while (son[x][1]) x=son[x][1];//不停往右子树查找splay(x);return x;//找到了，Splay到根后返回
}

查询k的后继 nxt()

$k$的后继是大于$k$中的所有数中最小的那个，操作很查询前驱很类似，就不多说了

inline int nxt()
{int x=son[root][1];//先查找到右子树while (son[x][0]) x=son[x][0];//不停往左子树查找splay(x);return x;//找到了，Splay到根后返回
}

删除操作 del(k)

此操作也是一个代码比较长比较复杂的操作，具体操作如下：
首先将$k$旋转到根的位置（用一个rk操作就行了），然后

• 如果权值出现次数大于1，则将权值出现次数减一就行了
• 否则合并当前节点的左右子树

而合并两棵$Splay$的规则是（假设要合并根节点为$x$和$y$的两棵$Splay$）：

• 如果$x$和$y$其中之一是空树或者都是空树，则返回非空树的根节点或者空树
• 否则将$x$子树中的最大值$Splay$到根，再以这个节点为根节点，将$y$赋值为它的右子树，更新信息再返回

很显然这仍然符合$Splay$的性质

inline void del(int k)
{rk(k);//将节点k旋转到根节点if (tot[root]>1) {--tot[root];maintain(root);return;}//权值出现次数大于1，则减一返回if (!son[root][0] && !son[root][1]) {clear(root);root=0;return;}//两棵空树,即销毁根节点返回if (!son[root][0]) {int x=root;root=son[x][1];fa[root]=0;clear(x);return;}if (!son[root][1]) {int x=root;root=son[x][0];fa[root]=0;clear(x);return;}//其中一个为空树，直接返更新信息，返回非空树int x=root,pre1=pre();//否则把左子树中最大的找出来（即跟的前驱）fa[son[x][1]]=pre1;son[pre1][1]=son[x][1];//将节点x的右子树赋值为yclear(x);maintain(root);//销毁节点x，更新根节点信息
}

总CODE（是以上代码的整合压行版）

#include<cstdio>
#include<string>
#define R register int
#define N 100005
using namespace std;
int n,son[N][2],fa[N],cnt,tot[N],size[N],root,val[N];
inline void read(int &x)
{x=0;int f=1;char ch=getchar();while (!isdigit(ch)) {if (ch=='-') f=-1;ch=getchar();}while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();x*=f;
}
inline void maintain(int x) {size[x]=size[son[x][0]]+size[son[x][1]]+tot[x];}
inline bool get(int x) {return x==son[fa[x]][1];}
inline void clear(int x) {size[x]=fa[x]=son[x][0]=son[x][1]=tot[x]=val[x]=0;}
inline void rotate(int x)
{int y=fa[x],z=fa[y],k=get(x);son[y][k]=son[x][k^1];fa[son[x][k^1]]=y;son[x][k^1]=y;fa[y]=x;fa[x]=z;if (z) son[z][son[z][1]==y]=x;maintain(x);maintain(y);
}
inline void splay(int x)
{for (R y=fa[x];y;rotate(x),y=fa[x]){if (fa[y]) rotate(get(x)==get(y)?y:x);}root=x;
}
inline void ins(int k)
{if (!root){val[++cnt]=k;++tot[cnt];root=cnt;maintain(root);return;	}int x=root,y=0;while (1){if (val[x]==k){++tot[x];maintain(x);maintain(y);splay(x);break;}y=x;x=son[x][val[x]<k];if (!x){val[++cnt]=k;++tot[cnt];fa[cnt]=y;son[y][val[y]<k]=cnt;maintain(cnt);maintain(y);splay(cnt);break;}}
}
inline int rk(int k)
{int res=0,x=root;while (1){if (k<val[x]) x=son[x][0];else{res+=size[son[x][0]];if (k==val[x]) {splay(x);return res+1;}res+=tot[x];x=son[x][1];}}
}
inline int kth(int k)
{int x=root;while (1){if (son[x][0] && k<=size[son[x][0]]) x=son[x][0];else{k-=size[son[x][0]]+tot[x];if (k<=0) {splay(x);return val[x];}x=son[x][1];}}
}
inline int pre()
{int x=son[root][0];while (son[x][1]) x=son[x][1];splay(x);return x;
}
inline int nxt()
{int x=son[root][1];while (son[x][0]) x=son[x][0];splay(x);return x;
}
inline void del(int k)
{rk(k);if (tot[root]>1) {--tot[root];maintain(root);return;}if (!son[root][0] && !son[root][1]) {clear(root);root=0;return;}if (!son[root][0]) {int x=root;root=son[x][1];fa[root]=0;clear(x);return;}if (!son[root][1]) {int x=root;root=son[x][0];fa[root]=0;clear(x);return;}int x=root,pre1=pre();fa[son[x][1]]=pre1;son[pre1][1]=son[x][1];clear(x);maintain(root);
}
int main()
{read(n);for (R i=1;i<=n;++i){int opt,x;read(opt);read(x);if (opt==1) ins(x);else if (opt==2) del(x);else if (opt==3) printf("%d\n",rk(x));else if (opt==4) printf("%d\n",kth(x));else if (opt==5) ins(x),printf("%d\n",val[pre()]),del(x);else ins(x),printf("%d\n",val[nxt()]),del(x);}return 0;
}

结语

终于写完了累死我了呼这篇博客我写得很用心，相信大家认真看都能初步入门$Splay$吧，如果有问题可以在评论区提出，博主活着的话都会解答哦，如果有太高级的问题，等到本蒟蒻多进行钻研之后也会回答，白白……