qwq表示最近感受到了不停课的鸭梨啊,好难搞啊……算法太难学了……我好菜啊qwq
其实半个多月前就可以写这篇文章,不过由于时间紧张没写emmmmmm,不扯闲言乱语了,如果有什么写的不好的地方凑活一下吧2333333333
splay是一种可以使树的最大深度尽可能的维持在logn级别的一种数据结构,当然splay的平衡确实不是非常好,但是它胜在代码量和思维难度小(像我这种菜鸡学个splay就快gg了),适合于算法竞赛,它中文名又叫伸展树,这也体现了它除平衡外的另一种特性——便于分裂和合并,这也可以利用splay方便的在序列上搞事情。
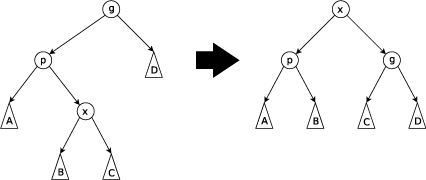
介绍完splay的特性,再来说它是如何维护平衡的。splay通过左旋和右旋这两种最基本的操作组合成共6种旋转模式,当然我们可以通过一些判断来简化旋转模式,接下来先讲一下基本操作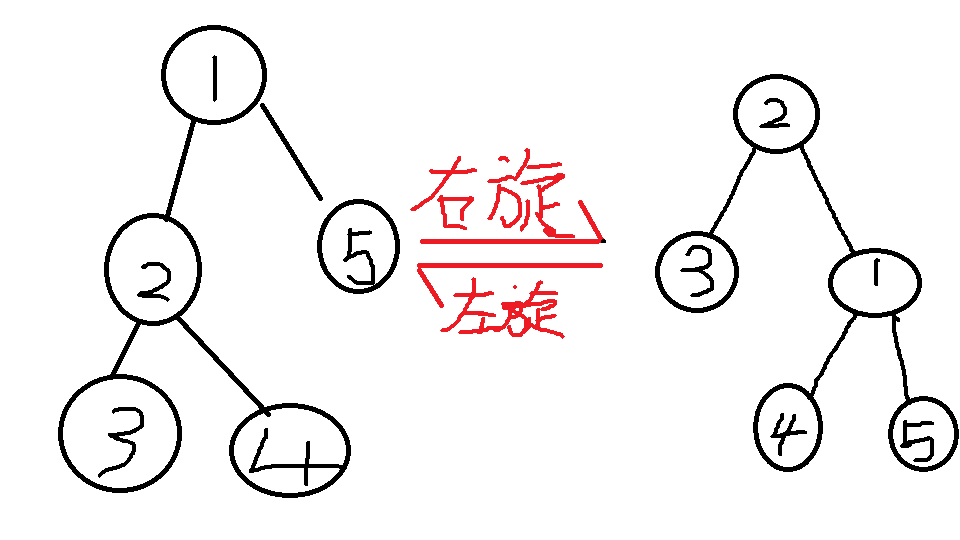
通过这张图我们可以看出,一个节点旋转的方向是由自己对于父亲的位置决定的,左蛾子向右转,右蛾子向左转,因此我们不需要刻意判断单次旋转方向
接下来说最重要的操作:splay
splay是这个数据结构最为重要的操作,是这棵树保持平衡的前提(虽然splay平衡效率不高),它是由多次旋转组合而来,每次我们考虑一个点和它的父亲、祖父,对着三个点进行操作,直至这个点到达根部,因为我们刚才把单次旋转简化,不用判断左旋还是右旋,所以splay的操作也简化成了两种:三个点同方向或者不同方向
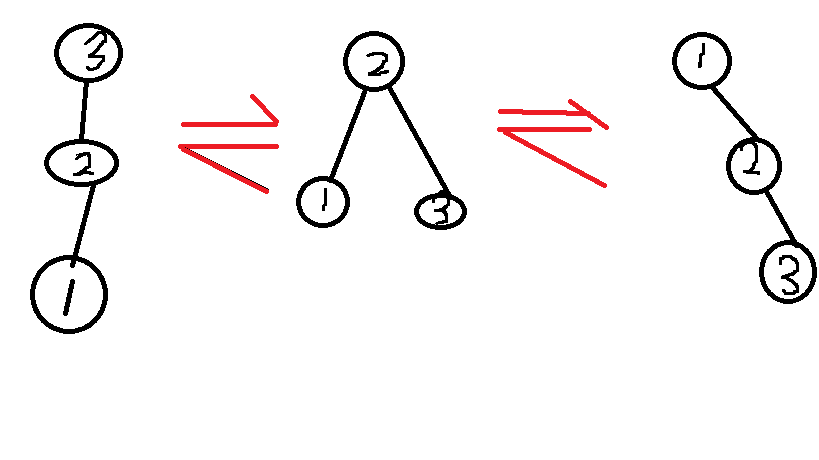
第一种,三个点同方向,那么先旋转它的父亲(因为旋转是为了让某个节点更加靠近根部,令其向上),然后再旋转它自身

第二种,三个点不同方向,一直旋转自己
splay本身作为一种二叉搜索树,可以满足logN查询前驱后继、第k名和k数字的排名,而且代码复杂度小,还支持快速分裂合并序列(待补),缺点是常数贼大,容易被卡
所以考虑学一个奇奇怪怪的平衡树……
至于代码
http://www.cnblogs.com/Loi-dfkdsmbd/p/8449498.html