例题：

给出一个长度为n序列a。
有m次操作，每次操作可以修改a[i]，在第i个数前插入一个数x，或查询区间[l,r]的最大值。

1≤n≤100000,1≤m≤100000。

强制在线

看到这道题最自然的反应就是用线段树，但有了插入操作线段树就不好处理了，需要离线才能做。而题目又要求强制在线，我们就只能使用splay了

---

什么是splay？

• splay是一棵二叉搜索树，满足一个节点右子树的所有节点小于它，而左子树的所有节点大于它。
• splay通过旋转它的节点来实现插入，查询区间极值、第K大值等操作。

---

旋转

旋转在splay当中是最基本的操作，splay就是通过对树的旋转来实现其他操作的。
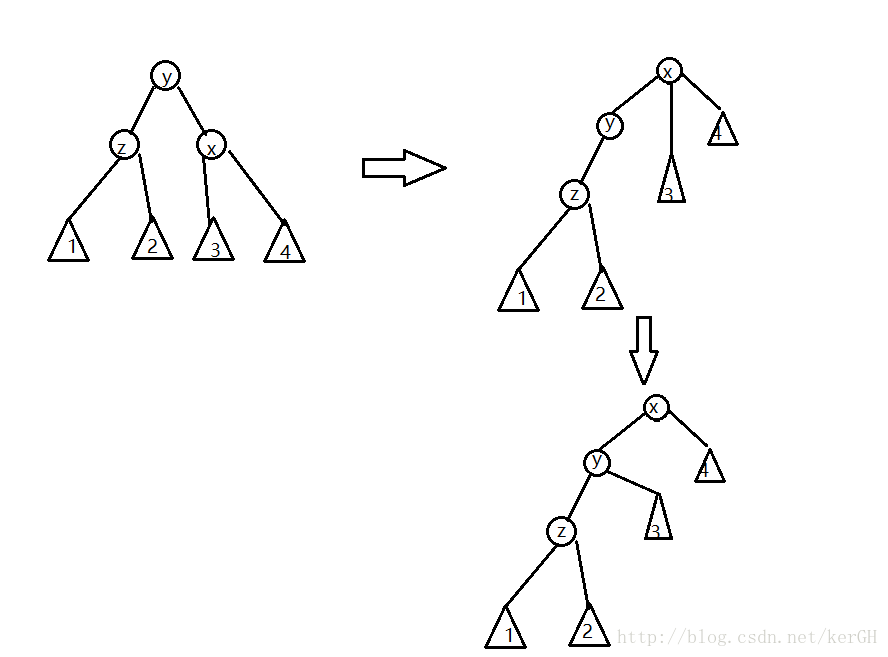
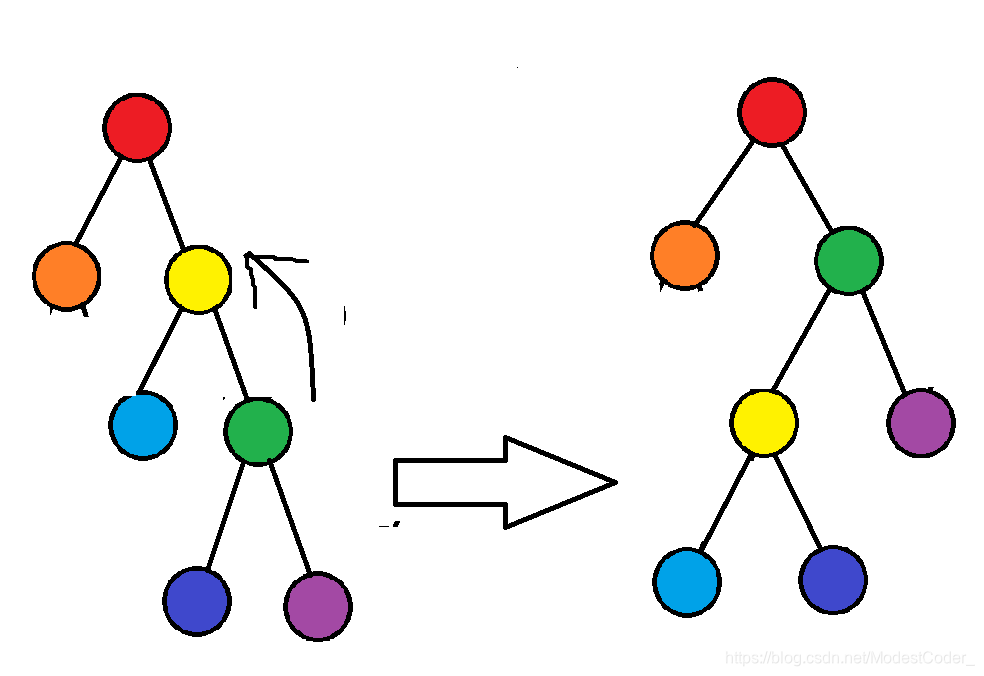
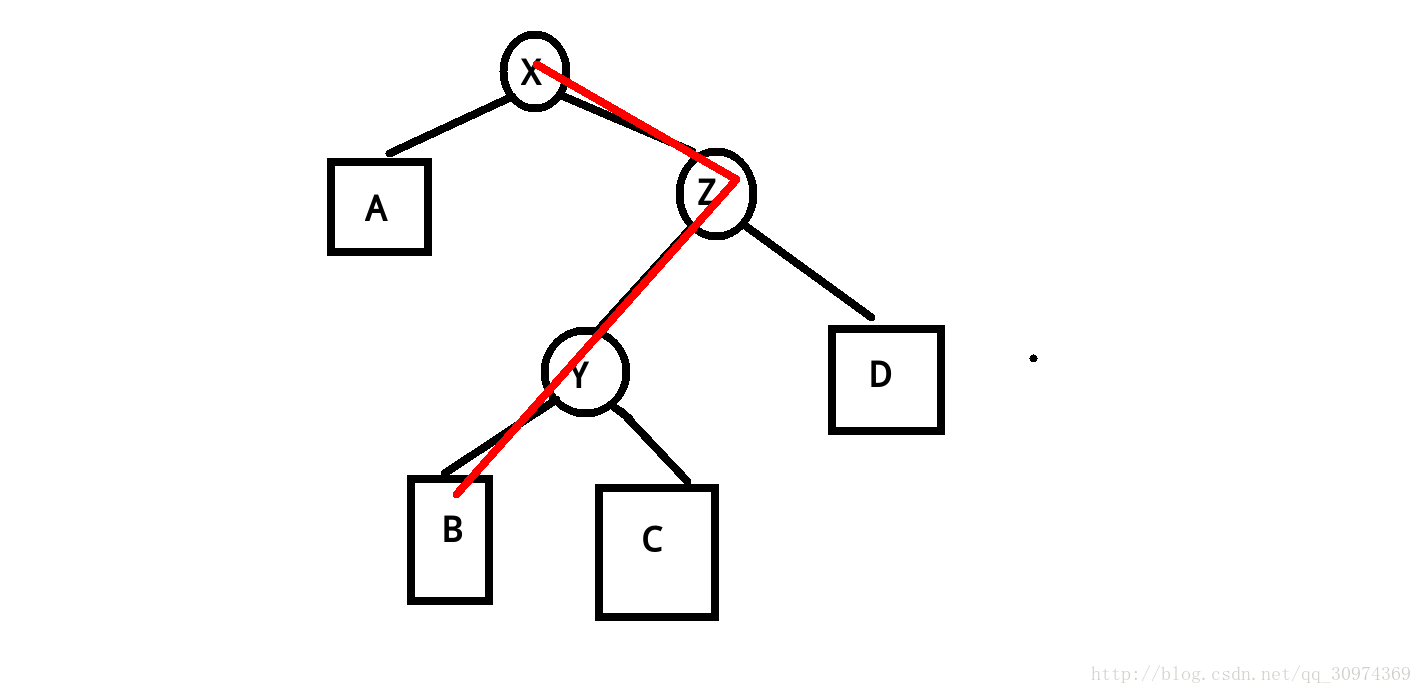
如图，将节点Y旋转到X。如果直接旋转，那么X就有了三个子节点，不再是一棵二叉树。因为splay是一棵二叉搜索树，所以在子树3中的节点都是大于节点Y的。我们可以把子树3的父节点指向Y，从而保证这是一棵二叉树。
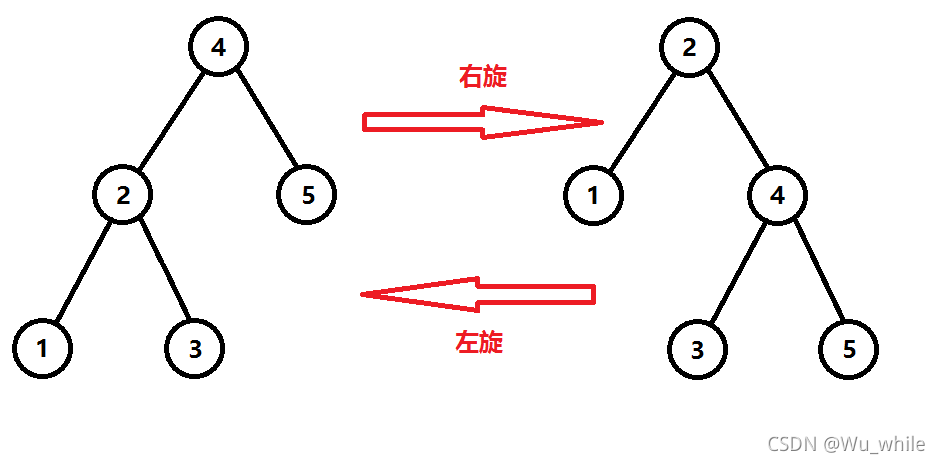
右旋为zig，左旋为zag，图中给出的是左旋。

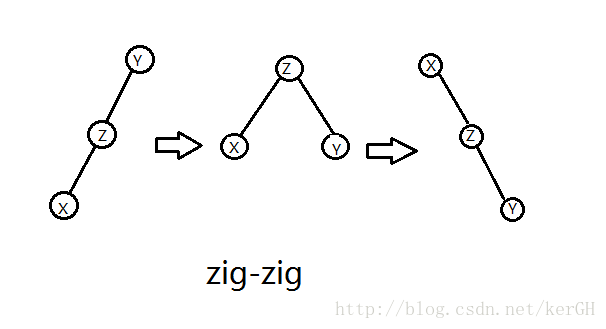
• zig-zig

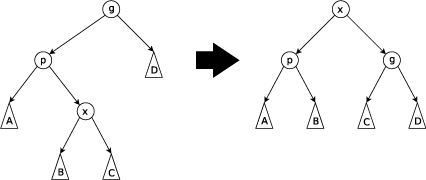
  如图，将X旋到Y，先左旋Z，在左旋X，也就是zig-zig，与之对应的操作是zag-zag。
  

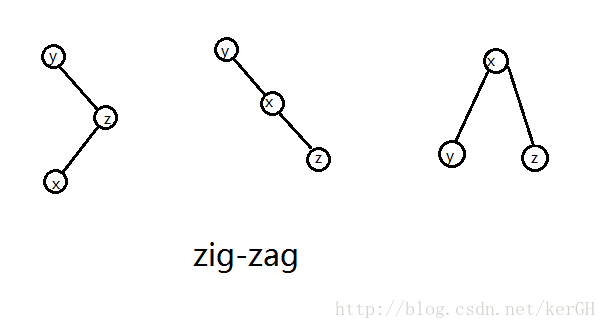
• zig-zag

  当要旋转时为下图的情况，应先zig(x),再zag(x)。同样，如果反过来，便是zag-zig。
  

其实可以完全不用管旋转的顺序，但按照上文的方式去旋转会快很多，均摊$log(n)$。这个tarjan会证。
如果不是很理解，可以画一下图，手玩一下。

在知道如何修改后，就可以用splay实现其他操作了。
接下来会介绍几个常用操作。

---

修改

单点修改就不说了，直接改变节点的值就可以了，这里我们讲区间修改。
如果要将一个序列上x~y全部加上一个数Z，怎么办？
将x-1旋到根，再将y+1旋到x-1的子节点。这时，y+1的右子树便是x~y的全部节点，我们再这棵子树的根上打一个tag即可。

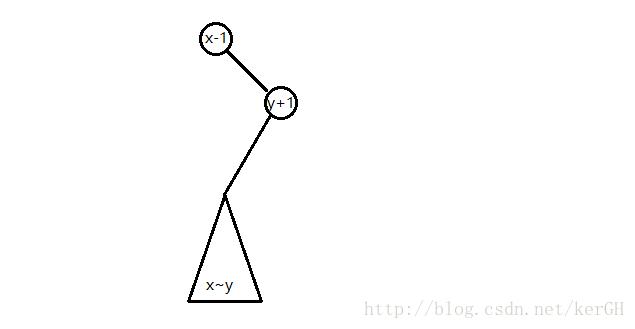
再每一次旋转的时候，记得要把tag下传，旋转完了还要updata。

---

插入

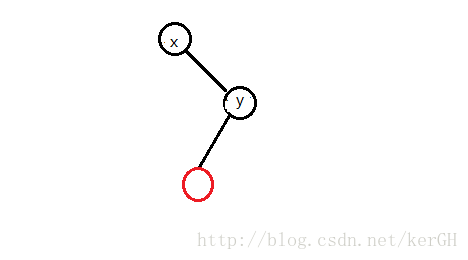
要在x和y之间插入一个数$(x<y)$，按照上面的思路，将x旋到根，再将y旋到x的子节点。
我们发现，y的右节点是空的，这时直接插入一个数就好了。

---

第k大值

要处理第k大值，对于一个节点x，我们多维护一个值size[x]，表示以节点x为根的这个子树大小。

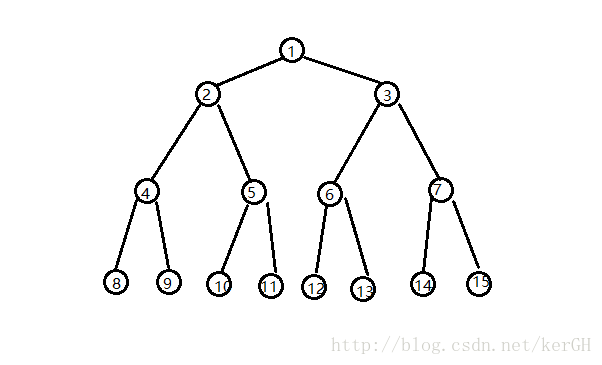
对上图来说，我们要查询第10大值。
size[2]+节点1+size[12]=8+1+1=9
所以节点6就是就是第10大值。

---

翻转

将区间L~R中的元素翻转，如图：

貌似不好实现……
根据区间修改的套路，我们将L-1旋的根，R+1旋到L-1的子节点，那么R+1的左子树就是区间L~R。
将splay中的一个节点的儿子节点对调，其实就是将这个节点在序列中左边和右边对调（自己脑补一下）
所以将这棵子树中的每一个节点对调即可实现翻转。

---

其实splay理解起来并不难，主要知道如何旋转就可以了，但实现起来会略微有点复杂。
这里给出splay的模板。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define LL long long 
#define isR(x) (b[f[x]][1]==x)
using namespace std;
const LL N=200001;
LL n,m,a[N],f[N],b[N][2],s[N],rmd[N],c[N],root,tag[N];
LL build(LL l,LL r)
{if (l>r) return 0;LL mid=(l+r)/2;rmd[mid]=1;s[mid]=r-l+1;if (l!=r){b[mid][0]=build(l,mid-1);b[mid][1]=build(mid+1,r);f[b[mid][0]]=f[b[mid][1]]=mid;c[mid]=max(max(c[b[mid][0]],c[b[mid][1]]),a[mid]);}else c[mid]=a[mid];return mid;
}
void update(LL x)
{s[x]=s[b[x][0]]+s[b[x][1]];c[x]=max(max(c[b[x][0]]+tag[b[x][0]],c[b[x][1]]+tag[b[x][1]]),a[x]*rmd[x]);
}
void put(LL x)
{if (tag[x]==3 && x==4)printf("");tag[b[x][0]]+=tag[x];tag[b[x][1]]+=tag[x];a[x]+=tag[x];tag[x]=0;
}
void rotate(LL x) {LL y=f[x],z=isR(x);put(y);put(x);b[y][z]=b[x][z^1];if (b[x][z^1]!=0) f[b[x][z^1]]=y;f[x]=f[y];if (f[y]!=-1) b[f[y]][isR(y)]=x;b[x][z^1]=y;f[y]=x;update(y);
}
void splay(LL x,LL y) {if (y==-1) root=x;while (f[x]!=y){if (f[f[x]]!=y){if (isR(x)!=isR(f[x])) rotate(x); else rotate(f[x]);}rotate(x);}update(x);
}
int main()
{//freopen("1.in","r",stdin);//freopen("1.out","w",stdout);memset(c,-0x7f,sizeof(c));LL i,j,k;scanf("%lld",&n);for (i=1;i<=n;i++) scanf("%lld",&a[i+1]);root=build(1,n+2);rmd[1]=0;rmd[n+2]=0;f[root]=-1;scanf("%lld",&m);for (i=1;i<=m;i++){LL x;scanf("%lld",&x);if (x==1) {LL l,r,y;scanf("%lld%lld%lld",&l,&r,&y);l++;r++;splay(r+1,-1);splay(l-1,r+1);LL z=b[l-1][1];tag[z]+=y;}else{LL l,r;scanf("%lld%lld",&l,&r);l++;r++;splay(r+1,-1);splay(l-1,r+1);printf("%lld\n",c[b[l-1][1]]+tag[b[l-1][1]]);}}
}

如果有不懂的地方，或文章有错误，可在评论留言。