前言

暑假快过完了,大家感觉是不是很棒!gay房也体验过最新的断电模拟器了.
好吧,在开讲之前我还是得说一个.刀剑神域的外传实在太好看了!
除了精彩的战斗场面,神一般的人设和强大的剧情,比起前作来看又多了一样我最喜欢的东西.
神曲!我从一名听众到神崎艾莎的粉丝只经过了一首歌.
Independence.燃到甚至有点伤感.看过作品的人应该能懂歌曲中隐含的感情.
我是一边听这首歌一边写的这个博客,大家也可以一边听歌一边欢乐地享受这一讲的内容.
好了讲正事.终于要开始研究神奇的数据结构了.
至于讲哪个,题目已经说了,我也就不扯淡了.
其实splay还是非常好懂的.
至于线段树什么的我自己也是先贺了一遍代码然后写一遍博客,只要3个月不学自会.
现在离AFO也差不多3个月,大概是能够会的.

splay出现的背景

大家都知道二叉查找树有概率会退化成链,这样时间复杂度就会大大增高.
这个时候有个叫Robert Tarjan 的男人和另一个叫Daniel Sleator的人发明了这样的一种数据结构.
它在每次询问的时候可以将树旋转(也就是splay这个操作)来维护树的平衡性.

它的操作

我们就以模板[普通平衡树]为例来学习这种数据结构.
那么这种数据结构应该要支持插入删除,求第$k$大,求排名,求前驱和后继.
首先我们定义struct splaytree.

const int yuzu=1e5;
typedef int fuko[yuzu|10];
/*事先准备maxsize和大小为maxsize的数组.*/
struct splaytree{
fuko ch[2],sz,cnt,fa,val;
/*ch是孩子,标号0,1分别表示左孩子和右孩子;sz是这个节点的子树大小(包括自己);cnt是这个节点保存的相同的值的个数(万一出现同样的数字只要cnt[u]++就可以了);fa是节点的父亲;val是节点保存的值.按照本题的要求来讲开这一些数组就够了.*/
然而我还要define一些东西.
#define ls(x) ch[0][x]
#define rs(x) ch[1][x]
#define ws(x,y) (rs(x)==y)
/*这个是which_son的简称,就是看y是x的左孩子还是右孩子.如果x的右孩子等于y,返回1.接下来会很骚,还请注意.*/
}my_;//开一棵名字叫做my_的splay树.当然要取名为其他东西也是可以的.

注:接下来为了巩固splay的知识,我都直接在代码框里手打代码,如果出现错误还望大家指出.
如果你也初学splay,贺代码请谨慎,出现错误,我不背这个锅.

push_up

void push_up(int u){sz[u]=sz[ls(u)]+sz[rs(u)]+cnt[u];/*这个操作解释不用很多,就是左孩子的子树大小+右孩子的子树大小+节点u包含相同字的个数.*/}

rotate

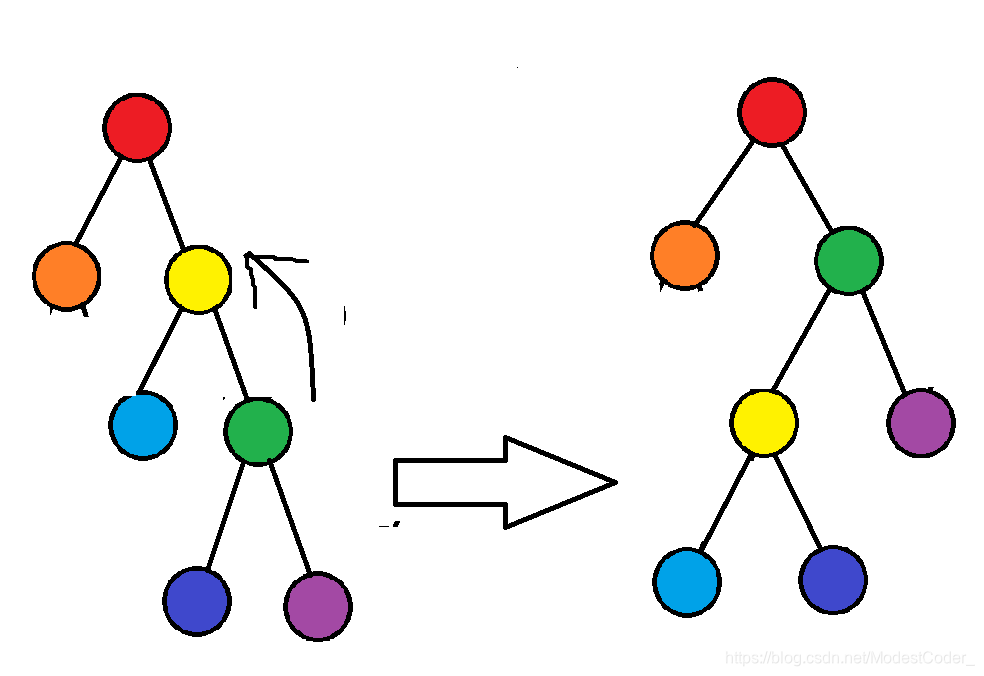
这个直接把代码放上来只有神仙能看懂.我该画图解释.
注意:二叉查找树满足左孩子权值小于节点权值,而右孩子权值严格大于节点的权值,以下图片中显现的是节点编号而不是节点权值.

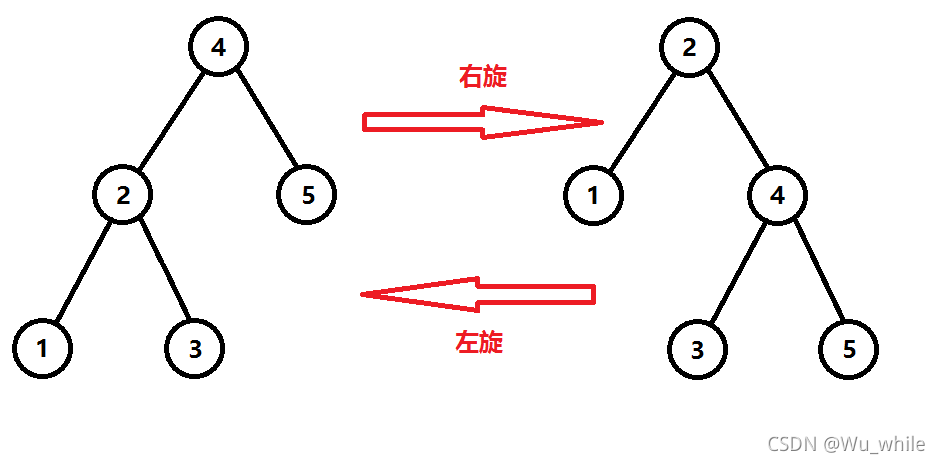
看上图,我们现在要把节点$4$旋转到$2$的位置,为了使它仍然满足二叉查找树的性质,我们来操作一下.
旋转完的树应该是这样的.

给每个节点代个权值进去会发现它仍然满足二叉树的性质.
我们不妨来找旋转的规律.

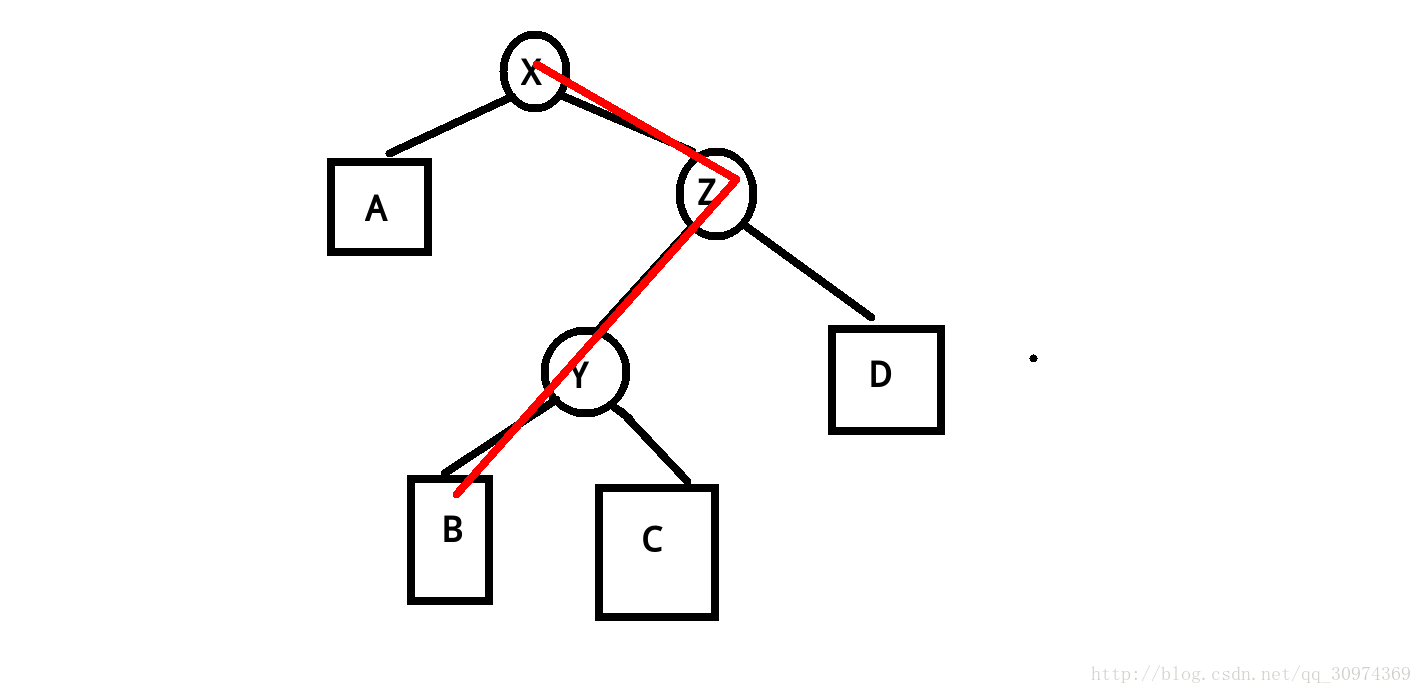
首先假设要旋转的节点是x,它的父亲是y,祖父是z.
我们先找出x与y的关系(左右儿子).
然后必然满足的条件:
1.x的x相对于y的子树不变.
2.x的相对于x相对于y的子树变成了y的x相对于y方向的子树.(仔细思考)
3.x的父亲变成z,y变成相对于x原来相对于y的儿子.

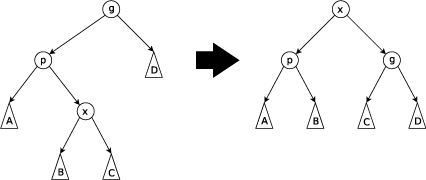
接下来写出旋转的代码,可结合上图分析使用.

void zhuan(int x){//rotateint y=fa[x],z=fa[y],k=ws(y,x);//取父亲和祖父,求x是y的哪一个儿子.ch[ws(z,y)][z]=x,fa[x]=z;/*z的y原来相对于z的儿子变成x,x的父亲变成z.*/ch[k][y]=ch[k^1][x],fa[ch[k^1][x]]=y;/*x的与原来x相对于y的方向相反的儿子变成y的x相对于y方向的儿子,同理赋值父亲.*/ch[k^1][x]=y,fa[y]=x;/*y变成x的与原来x相对于y相反方向的儿子,y的父亲变成x.*/push_up(y),push_up(x);/*push_up一下.*/}

给你们10分钟时间听歌思考.
……

splay

该树最核心的操作之一────splay操作出现了.
如果你能够理解上面的旋转操作我们就直接上代码了.

void splay(int x,int g){//将x旋转成为g的儿子,如果g是0则将x旋转到根. for (;fa[x]^g;zhuan(x)){//最后一定会旋转一次x int y=fa[x],z=fa[y];if (z^g) zhuan(ws(z,y)^ws(y,x)?x:y);//如果z不是根就额外转一次./*通过判断y是z的哪个儿子和x是y的哪个儿子的关系决定是旋转y还是x.其实分类讨论zig,zag也是这样的算法,非常麻烦,用这个就很简单了.*/ }if (!g) rt=x;//如果g等于0将x设为根. }
/*这些操作的意图都是使树变得平衡.*/

find

把维护splay平衡的代码写完了,终于到询问的时候了.
这个操作能够找到存放大小为$x$的数字的那个节点,并把这个节点splay到根.

void find(int x){int u=rt;if (!u) return;//rt为0,该树中没有点,直接跳出.for (;ch[x>val[u]][u]&&val[u]^x;)u=ch[x>val[u]][u];/*根据二叉查找树的性质,根据x关于左右儿子存放的值的关系在左右儿子中查找.注意特判x恰好和u存放的值相等的情况.*/splay(u,0);//将u节点splay到根,为求x是第几大的数字做铺垫.}

insert

插入一个节点.

void insert(int x){int u=rt,nf=0;//nf是现在u的父亲.for (;u&&val[u]^x;) nf=u,u=ch[x>val[u]][u];//按顺序找x应该在的位置.if (u) ++cnt[u];//如果已经存在x,将cnt++.else{//不存在,新开一个节点.u=++tot;if (nf) ch[x>val[nf]][nf]=u;ls(u)=rs(u)=0;fa[u]=nf,val[u]=x,cnt[u]=1,sz[u]=1;}splay(u,0);//不要忘记splay到根,保持树的平衡性.}

next

前驱和后继.

int next(int x,int f){//f前驱为0,后继为1find(x);int u=rt;if (val[u]>x&&f||val[u]<x&&!f) return u;/*find过后val[u]如果不等于x,它一定是最接近x的那个数,如果此时val[u]比x大或者小满足要求的前或者后,就可以直接判断前驱后继.*/u=ch[f][u];//先往u向f的那个方向跳一个儿子.for (;ch[f^1][u];) u=ch[f^1][u];/*接下来一直往反方向跳,就可以得到比x大的最小的数或者比x小的最大的数.*/return u;}

delete

借助next可以完成删除操作.

void del(int x){int lat=next(x,0),net=next(x,1);/*定义last为x的前驱,next为x的后继.*/splay(lat,0),splay(net,lat);/*把last转到根,next转到last的右儿子.显然一定是转到右儿子.*/int nde=ls(net);//那么值为x的节点此时应该是next的左儿子.if (cnt[nde]>1){//cnt[nde]>1的话可以只是删掉一个.cnt[nde]--;splay(nde,0);//转到根节点.}else ls(net)=0; }

findkth

最后是找第k大值.

int kth(int x){int u=rt;if (sz[u]<x) return 0;/*如果sz[u]<x说明整棵树里没有k个值,也当然没有第k大.*/for (;;){int y=ls(u);if (x>sz[y]+cnt[u]){x-=sz[y]+cnt[u];u=rs(u); }else if (sz[y]>=x) u=y;else return val[u];}//这一部分分类讨论估计也不用讲了.}

main

main包就很简单了.

int main(){
my_.insert(-1e7-4);
my_.insert(1e7+4);
n=read();
for (;n--;){int op=read();switch(op){case 1: my_.insert(read()); break;case 2: my_.del(read()); break;case 3: my_.find(read()),write(my_.sz[my_.ls(rt)]),pl; break;case 4: write(my_.kth(read()+1)),pl; break;case 5: write(my_.val[my_.next(read(),0)]),pl; break;case 6: write(my_.val[my_.next(read(),1)]),pl; break;}}
}

预告:接下来会写LCT.
谢谢大家.