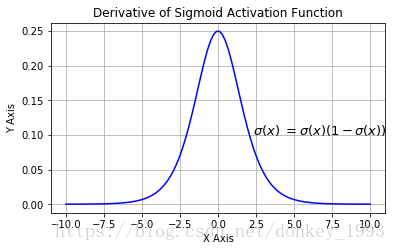
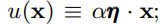GELU激活函数

最近看bert论文，发现用的是GELU激活函数，找出来看看

论文：GAUSSIAN ERROR LINEAR UNITS (GELUS)
项目：https://github.com/hendrycks/GELUs

ABSTRACT

本文提出了高斯误差线性单元(GELU)，一个高性能的神经网络激活函数。GELU激活函数为 $x Φ (x)$ ，其中 $Φ (x)$ 为标准高斯累积分布函数。GELU非线性根据输入的值来权重，而不是像ReLUs( $x1_{x>0}$ )那样通过符号来门输入。本文对ReLU和ELU激活的GELU非线性进行了实证评估，发现在计算机视觉、自然语言处理和语音任务都有性能改进。

1.INTRODUCTION

早期的人工神经元使用二元阈值单位(Hopfield，1982)。这些硬的二进制决策被s型激活来平滑，使神经元能够有一个“放电率”的解释，并通过反向传播进行训练。但随着网络的越来越深入，s型激活训练被证明不如非平滑、概率较低的ReLU(Nair&Hinton，2010)，后者根据输入的符号做出hard门控决策。尽管随着网络变得更深，但ReLU仍然是一个具有竞争力的工程解决方案，它通常能够比s型符号更快更好地收敛。在ReLUs成功的基础上，最近一种名为ELUs的修正阳离子(Clevertetal.，2016)允许类似relu的非线性能够输出负值，有时会提高训练速度。总之，激活选择仍然是神经网络必要的结构决策，避免网络是一个深度线性分类器。

深度非线性分类器可以很好地拟合他们的数据，以至于网络设计者经常面临包括随机正则化的选择，比如向隐藏层添加噪声或应用dropout(Srivastavaetal.，2014)，而且这种选择仍然与激活函数分离。一些随机正则化器可以使网络表现得像一个网络集合，一个伪集成(Bachmanetal.，2014)可以导致显著的精度提高。例如，随机正则化dropout通过通过零乘法随机改变一些激活决策来创建一个伪集成。非线性和dropout共同决定了一个神经元的输出，但这两种创新仍然是不同的。此外，两者都不包含另一种，因为流行的随机正则化分别与输入无关，而非线性得到了这些正则化的帮助。

在本文中，引入了一种新的非线性，高斯误差线性单元(GELU)。它与随机正则化有关，因为它是对自适应dropout修改的期望(Ba&Frey，2013)。这表明了对神经元输出的更有概率的观点。我们发现，在计算机视觉、自然语言处理和自动语音识别等领域，新型非线性激活函数达到的性能与relu或elu相匹配或更胜一筹。

2 GELU FORMULATION

我们通过结合来自dropout、区域输出和relu的属性来激发提出新型激活函数。首先注意到，ReLU和dropout都产生一个神经元的输出，ReLU确定地将输入乘以0或1，dropout随机乘以零。此外，一种名为区域输出的新的RNN正则化（zoneout）会随机乘以输入(Krueger等人，2016)。我们通过将输入乘以0或1来合并这个功能，但是这个zero-one掩模的值是随机确定的，同时也依赖于输入。具体来说，可以将神经元输入 $x$ 乘以 $m \sim B e r n o u l l i (Φ (x))$ ，其中 $Φ (x) = P (X \leq x) N (0, 1)$ 为标准正态分布的累积分布函数。我们选择这种分布是因为神经元输入倾向于遵循正态分布，特别是与批归一化。在这种情况下，随着x的减小，输入被“下降”的概率更高，因此应用于x的变换是随机的，但却取决于输入。

包含非确定性，但保持对输入值的依赖性。一个随机选择的掩模相当于输入的随机零或身份变换，这很像自适应dropout，但自适应dropout是与非线性一起使用，并使用逻辑函数而非标准的正态分布。本文发现，可以仅使用这个随机正则化训练MNIST和TIMIT网络就能取得比较好的效果，且不使用任何非线性。
在这里插入图片描述

我们通常想要一个来自神经网络的确定性判断，这就产生了本文提出新的非线性。非线性是随机正则化在输入 $x$ 上的期望变换，即 $Φ (x) \times I x + (1 - Φ (x)) \times 0 x = x Φ (x)$ 。简单地说，这个表达式表示放大输入x。由于高斯误差的累积分布函数通常用误差函数计算，因此将高斯误差线性单位(GELU)定义为

$\frac{1}{2} [ 1 + erf(x/√ 2)]$
我们可以用下面式子表示:
$tanh[\sqrt{2/π}(x + 0.044715x^3)])$
或者
$x σ (1.702 x)$

更快的前馈速度一般会导致精度的降低。
我们可以使用不同的cdf。例如，可以使用逻辑分布CDF $σ (x)$ 来得到 Sigmoid Linear Unit (SiLU) $ xσ(x)$。可以使用CDF $N (µ ， σ 2)$ ，并使µ和σ是可学习的超参数，但在整个工作过程中，简单地让µ=0和σ=1。因此，在接下来的实验中没有引入任何新的超参数。在下一节中，将展示GELU在许多任务中的表现超过了ReLUs和ELUs。

3 GELU EXPERIMENTS

本文在以下任务中评测了GELU，ELU和ReLU的性能：

MNIST分类(包含10个类、60k训练示例和10k测试示例)
MNIST 自动编码器
Tweet上的部分语音标签（1000条训练、500条测试样本）
TIMIT帧识别（3696条训练、1152个验证、192个测试音频句）
CIFAR-10/100分类(10/100类、50k训练和10k测试示例的彩色图像)
本文没有评估像LReLU这样的非线性，因为它与ReLUs相似。

3.1 MNIST CLASSIFICATION

在这里插入图片描述

通过复制Clevert等人的实验来验证这种非线性与之前的激活函数的表现。（2016）。为此，用GELUs（µ=0，σ=1）、ReLUs和ELUs（α=1）训练了一个全连接的神经网络。8层，每层128个神经元的神经网络被训练50个时代，BatchSize大小为128。这个实验不同于Clevert等人。在此过程中，使用了Adam优化器(Kingma&Ba，2015)，而不是没有动量的随机梯度下降（SGD），此外还展示了非线性如何很好地应对dropout。权重用归一化范数行初始化，因为这对每个非线性的性能都有积极影响（Hendrycks&Gimpel，2016；Mishkin&Matas，2016；Saxe等人，2014）。使用来自训练集中的500个验证示例来调整学习速率 ${10^{−3}、10^{−4}、10^{−5}}$ ，并取5次运行的中位数结果。使用这些分类器，在图3中演示了使用GELU的分类器可以对噪声输入具有更强的鲁棒性。图2显示，无论s是否使用dropout还是不使用dropout，GELU的中位数训练对数损失往往是最低的。因此，尽管GELU的灵感来自于一个不同的随机过程，但它与退出很吻合。

3.2 MNIST AUTOENCODER

在这里插入图片描述

现在假设一个自监督设置，并在MNIST上训练一个深层自编码器。为了实现这一点，使用了一个层宽度为1000、500、250、30、30、250、500、1000的网络。再次使用Adam优化器和BatchSize为64，损失函数是均方损失。将学习率从 $10^{−3}$ 变化到 $10^{−4}$ ，也尝试了0.01的学习率，结果表明ELUs是发散，GELUs和RELUs收敛较差。图4中的结果表明，GELU适应不同的学习率，并显著优于其他非线性。

3.3 TWITTER POS TAGGING

自然语言处理中的许多数据集相对较小，因此从少数例子中很好地推广激活是很重要的。为了应对这一挑战，比较了 tweet的非线性(Gimpel等人，2011；Owoputi等人，2013)，其中包含25个标签。推文标记只是一个两层网络，预先训练的单词向量在5600万条推文库上训练的单词向量(Owoputietal.，2013)。输入是被标记的词的向量与其左右相邻词的向量的连接。每一层有256个神经元，dropout保持概率为0.8，使用Adam优化网络，同时调整学习速率 ${10^{−3},10^{−4},10^{−5}}$ 。我们对每个学习率每个网络训练5次，GELU的中值测试集误差为12.57%，ReLU为12.67%，ELU为12.91%。

3.4 TIMIT FRAME CLASSIFICATION

在这里插入图片描述

这次挑战是使用TIMIT数据集进行电话识别，该数据集在一个无噪音的环境下有680个扬声器的录音。该系统是一个五层，宽度为2048个神经元的分类器，如(Mohamed等人，2012)，有39个输出电话标签，dropout概率为0.5，如(Srivastava，2013)。这个网络以11帧作为输入，必须预测中心的电话。每帧使用26个MFCC、幅度和导数特征。调优了学习速率 ${10^{−3},10^{−4},10^{−5}}$ ，并使用Adam进行优化。每次设置后迭代5次，得到图5中的中值曲线，GELU最低验证误差选择的中值检验误差为29.3%，ReLU为29.5%，ELU为29.6%。

3.5 CIFAR-10/100 CLASSIFICATION

在这里插入图片描述

接下来，证明了对于更复杂的架构，GELU的非线性再次优于其他非线性。分别使用CIFAR-10和CIFAR-100数据集(Krizhevesk，2009)在浅层和深层卷积神经网络上评估这种激活函数。
浅层卷积神经网络是一个9层的网络，与saliman&Kingma（2016）的网络架构和训练程序一样，同时使用批归一化（BN）来加快训练速度。该架构在附录A中描述，没有使用数据增强来训练这个网络。用5k个验证示例调优学习初始速率 ${10^{−3},10^{−4},10^{−5}}$ ，然后根据交叉验证的学习率再次对整个训练集进行训练。用Adam优化了网络，共运行200个epoch，在第100个epoch，学习速率线性衰减为零。结果如图6所示，每条曲线都是三次运行的中位数。最终，GELU得到的中值错误率为7.89%，ReLU为8.16%，ELU得到8.41%。
接下来，考虑在CIFAR-100上运行一个宽的残差网络，有40层，拓宽因子为4(Zagoruyko&Komodakis，2016)。用内斯特洛夫动量(洛什奇洛夫&Hutter，2016)(T0=50，η=0.1)中描述的学习速率时间表来训练50个epoch，dropout保持概率为0.7。一些研究者注意到，ELUs在残差网络中有梯度爆炸性问题(Shahetal.，2016)，这可以通过在残差块末端进行批归一化得到缓解。因此，我们使用了一个连续激活-连续激活-批归一化体系结构来改善ELUs。经过三次运行，得到了图7中的中值收敛曲线。GELU的中值误差为20.74%，ReLU获得21.77%，ELU获得22.98%。

4 DISCUSSION

在几个实验中，GELU优于以前的非线性，但它在其他方面似乎接近ReLU和ELU。例如，当 $σ \to 0$ ，如果 $µ = 0$ ，GELU将成为一个ReLU。此外，ReLU和GELU渐近相等。事实上，GELU可以被视为一种平滑ReLU的方法，记住 $R e L U = m a x (x ， 0) = x 1 (x > 0) (其中 1 为指示函数)$ ，而如果 $µ = 0, σ = 1$ ，GELU为 $x Φ (x)$ 。然后CDF是ReLU使用的二进制函数的平滑近似，比如s型平滑二进制阈值激活。与ReLU不同，GELU和ELU既可以是阴性的，也可以是阳性的。事实上，如果使用标准柯西分布的累积分布函数，将线向下移动 $1 / π$ ，那么ELU（当α=1/π）渐近等于 $x P (C \leq x) ， C \sim C a u c h y (0, 1)$ 的负值和正值是 $x P (C \leq x)$ ，这些都表明GELu与以前的非线性之间的一些基本关系。
然而，GELU有几个显著的差异。这个非凸、非单调的函数在正域上不是线性的，在所有点上都表现出曲率。同时，凸激活和单调激活的EeLUs和ELUs在正域上是线性的，因此可能缺乏曲率。因此，增加的曲率和非单调性可能使基因比ReLUs或ELUs更容易近似复杂的函数。此外，由 $R e L U (x) = x 1 (x > 0)$ 和 $G E L U (x) = x Φ (x)$ ，如果 $µ = 0 ， σ = 1$ ，可以看到ReLU打开输入的符号依赖于它，而GELU对输入的权重取决于它比其他输入的大小。此外，更重要的是，GELU有一个概率解释，因为它是一个随机正则化器的期望。
此外还有两个使用GELU的实用技巧。首先，建议在使用GELU训练时使用具有动量的优化器，这是深度神经网络的标准。其次，使用对高斯分布的累积分布函数的密切近似是很重要的。一个s型函数 $σ(x)=1/(1+e^{−x})$ 是一个正态分布的累积分布函数的近似值。然而，我们发现西格莫德线性单元(SiLU) $x σ (x)$ 比GELUs差，但通常比ReLUs和ELUs好，所以SiLU也是一个合理的非线性选择。本文没有使用 $x σ (x)$ 来近似 $Φ (x)$ ，而是使用 $0.5x(1+tanh[\sqrt{2/π}(x+0.044715x^{3}))$ (choury（2014）或 $x σ (1.702 x)$ 。两者都是足够快、易于实现的近似。本文的每个实验中都使用了前者。

5. CONCLUSION

对于本文中评估的众多数据集，GELU始终超过了ELU和ReLU的准确性，使其成为以前非线性的可行替代方案。

REFERENCES

Jimmy Ba and Brendan Frey. Adaptive dropout for training deep neural networks. In Neural Information Processing Systems, 2013.
Philip Bachman, Ouais Alsharif, and Doina Precup. Learning with pseudo-ensembles. In Neural
Information Processing Systems, 2014.
Amit Choudhury. A simple approximation to the area under standard normal curve. In Mathematicsand Statistics, 2014.
Djork-Arn´e Clevert, Thomas Unterthiner, and Sepp Hochreiter. Fast and accurate deep network
learning by exponential linear units (ELUs). In International Conference on Learning Representations, 2016.
Guillaume Desjardins, Karen Simonyan, Razvan Pascanu, and Koray Kavukcuoglu. Natural neural networks. In arXiv, 2015.
Kevin Gimpel, Nathan Schneider, Brendan O0 Connor, Dipanjan Das, Daniel Mills, Jacob Eisenstein, Michael Heilman, Dani Yogatama, Jeffrey Flanigan, and Noah A. Smith. Part-of-Speech Tagging for Twitter: Annotation, Features, and Experiments. Association for Computational Linguistics (ACL), 2011.
Dan Hendrycks and Kevin Gimpel. Adjusting for dropout variance in batch normalization and
weight initialization. In arXiv, 2016.
John Hopfield. Neural networks and physical systems with emergent collective computational abilities. In Proceedings of the National Academy of Sciences of the USA, 1982.
Diederik Kingma and Jimmy Ba. Adam: A Method for Stochastic Optimization. International
Conference for Learning Representations, 2015.
Alex Krizhevsky. Learning Multiple Layers of Features from Tiny Images, 2009.
David Krueger, Tegan Maharaj, Jnos Kram´ar, Mohammad Pezeshki, Nicolas Ballas, Nan Rosemary Ke1, Anirudh Goyal, Yoshua Bengio, Hugo Larochelle, Aaron Courville, and Chris Pal. Zoneout: Regularizing RNNs by randomly preserving hidden activations. In Neural Information Processing Systems, 2016.
Ilya Loshchilov and Frank Hutter. SGDR: Stochastic gradient descent with restarts. arXiv, 2016.
Andrew L. Maas, Awni Y. Hannun, , and Andrew Y. Ng. Rectifier nonlinearities improve neural network acoustic models. In International Conference on Machine Learning, 2013.
Warren S. McCulloch and Walter Pitts. A logical calculus of the ideas immanent in nervous activity. In Bulletin of Mathematical Biophysics, 1943.
Dmytro Mishkin and Jiri Matas. All you need is a good init. In International Conference on Learning Representations, 2016.
Abdelrahman Mohamed, George E. Dahl, and Geoffrey E. Hinton. Acoustic modeling using deep belief networks. In IEEE Transactions on Audio, Speech, and Language Processing, 2012.
Vinod Nair and Geoffrey E. Hinton. Rectified linear units improve restricted boltzmann machines. In International Conference on Machine Learning, 2010.
Olutobi Owoputi, Brendan O’Connor, Chris Dyer, Kevin Gimpel, Nathan Schneider, and Noah A. Smith. Improved part-of-speech tagging for online conversational text with word clusters. In North American Chapter of the Association for Computational Linguistics (NAACL), 2013. 7
Tim Salimans and Diederik P. Kingma. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. In Neural Information Processing Systems, 2016.
Andrew M. Saxe, James L. McClelland, and Surya Ganguli. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. In International Conference on Learning Representations, 2014.
Anish Shah, Sameer Shinde, Eashan Kadam, Hena Shah, and Sandip Shingade. Deep residual networks with exponential linear unit. In Vision Net, 2016.
Nitish Srivastava. Improving neural networks with dropout. In University of Toronto, 2013.
Nitish Srivastava, Geoffrey E. Hinton, Alex Krizhevsky, Ilya Sutskever, and Ruslan Salakhutdinov. Dropout: A simple way to prevent neural networks from overfitting. In Journal of Machine Learning Research, 2014.
Sergey Zagoruyko and Nikos Komodakis. Wide residual networks. British Machine Vision Conference, 2016.