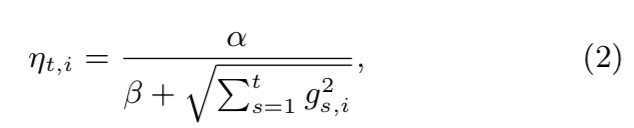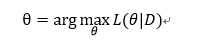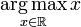契机

最近工作方向为缩减模型规模，切入点为L1正则化，选择该切入点的理由如下，

众所周知，L1正则化能令权重矩阵更稀疏。在推荐系统中特征多为embedding，权重矩阵稀疏意味着一些embedding_weight为0，模型部署时这些embedding不会导出，从而达到缩减模型规模的目的，这样做有3个好处：

性能更好：小模型部署快，这点对于实时训练很重要，因为较多时间会花在模型部署上，部署快意味着更快的模型迭代，
内存更小：这点毋庸置疑，
效果更好：在适当参数配置下，L1正则化干掉的特征一般不重要，这样模型被这些特征干扰的概率降低，效果会更好。

但是，随着随机梯度下降(SGD)的应用，L1正则化后的模型稀疏程度下降，理由正如冯扬大神所述。FTRL正是在这个环境下诞生的，其核心目的在于解决模型稀疏化问题。

备注：下文所有的稀疏性都为权重稀疏性。

发展历程

L1正则化

直接上权重更新公式：
$W^{(t+1)}=W^{(t)}-\eta^{(t)}G^{(t)}-\eta^{(t)}\lambda sgn(W^{(t)})$
其中 $W^{(t)}$ 代表训练第 $t$ 步时的权重， $\eta ^{(t)}$ 代表学习率， $G^{(t)}$ 代表梯度， $\lambda$ 代表L1正则化参数， $sgn(\cdot)$ 为符号函数，这里 $sgn(W_{(t)})$ 为 $W_{(t)}|$ 的导数。

简单截断法

既然L1正则化后的权重依然不为0，则直接在让权重在比较小时截断为0，这样在一定程度上直接解决稀疏化问题，具体公式如下，
$W^{(t+1)}=T_0(W^{(t)}-\eta ^{(t)}G^{(t)},\theta)$
其中 $T_0(v_i,\theta)$ 为截断函数，具体形式如下，
$T_0(v_i,\theta)=\left\{\begin{matrix} 0 \ \ \ \ if \ \left | v_i \right | \leq \theta\\ v_i \ \ \ \ otherwise \end{matrix}\right.$
实际操作时，如果 $t / k$ 不为整数时按正常SGD进行迭代，否则则采用上述公式进行权重更新。具体示意图如下所示，

TG

简单截断法太过暴力，参数控制不好效果会有损，之后便诞生了Truncated Gradient算法(简称为TG)，具体公式如下，
$W^{(t+1)}=T_1(W^{(t)}-\eta^{(t)}G^{(t)},\eta^{(t)}\lambda^{(t)},\theta)$
其中 $\lambda^{(t)}$ 为另一个限制阈值， $T_1(v_i,\alpha,\theta)$ 为TG算法的截断函数，具体形式如下，
$T_1(v_i,\alpha,\theta)=\left\{\begin{matrix} max(0,v_i -\alpha) \ \ \ \ \ \ \ \ \ if \ v_i \in \left [ 0,\theta \right ]\\ min(0,v_i +\alpha) \ \ \ \ \ \ if \ v_i \in \left [ -\theta,0 \right ]\\ v_i \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ otherwise \end{matrix}\right.$
实际操作时，类似简单截断法，每 $k$ 步截断一次，当 $t / k$ 不为整数时 $\lambda^{(t)}=0$ ，否则 $\lambda^{(t)}=k\lambda$ ，可以看出 $\lambda$ 和 $\theta$ 同时控制权重稀疏性，越大稀疏性越好。具体示意图如下所示，

根据上述讲解，可以看出TG可以变换为简单截断法，也可以转换为L1正则化，

TG -> 简单截断法

TG -> L1正则化

L1-FOBOS

更进一步，FOBOS核心思想是既考虑上一次迭代结果，也寻求本阶段最优，具体公式如下，
$\begin{matrix} W^{(t+\frac{1}{2})}=W^{(t)}-\eta^{(t)}G^{(t)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)\\ W^{(t)}=argmin_W\left \{ \frac{1}{2}\left \| W-W^{(t+\frac{1}{2})} \right \|^2+\eta^{(t+\frac{1}{2})}\Psi (W) \right \}\ \ \ \ \ (2) \end{matrix}$

上述公式中第(1)步为标准的随机梯度下降，第(2)步是在当前基础上对结果进行微调。经过一套复杂推导公式(此处省略一万个公式)，得到如下结果，
$w_i^{(t+1)}=sgn(w_i^{(t)}-\eta^{(t)}g_i^{(t)})max\left \{ 0,\left | w_i^{(t)}-\eta^{(t)}g_i^{(t)} \right | -\eta^{(t+\frac{1}{2})}\lambda\right \}$
公式的另一种展现形式为：
$w_i^{(t+1)}=\left\{\begin{matrix} 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \left | w_i^{(t)}-\eta^{(t)}g_i^{(t)} \right | \leq \eta^{(t+\frac{1}{2})}\lambda \\ \left ( w_i^{(t)}-\eta^{(t)}g_i^{(t)} \right )-\eta^{(t+\frac{1}{2})}\lambda sgn\left ( w_i^{(t)}-\eta^{(t)}g_i^{(t)} \right ) \ \ \ \ otherwise \end{matrix}\right.$
可以看出当一条样本产生的梯度，不足以令对应维度上权重产生足够大的变化，本维度不重要，权重被置为0，从而解决稀疏化问题。

L1-RDA

上述方法都是在随机梯度下降基础上进行改进的，而RDA另辟蹊径，具体公式如下，
$W^{(t+1)}=argmin_W\left \{ \frac{1}{t}\sum_{r=1}^t\left \langle G^{(r)},W \right \rangle +\lambda ||W||_1+ \frac{\gamma}{2\sqrt{t}}||W||^2_2\right \}$
其中 $\left \langle G^{(r)},W \right \rangle$ 为梯度 $G^{(r)}$ 对 $W$ 的积分平均值， $\lambda ||W||_1$ 为L1正则化项， $\left \{ \frac{\gamma}{2\sqrt{t}}|t \geq 1\right \}$ 为一个非负非递减序列。经过一套复杂推导公式(此处省略一万个公式)，得到如下结果，
$w_i^{(t+1)}=\left\{\begin{matrix} 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \left | \bar{g_i}^{(t)} \right |< \lambda \\ -\frac{\sqrt{t}}{\gamma}\left ( \bar{g_i}^{(t)}-\lambda sgn(\bar{g_i}^{(t)}) \right ) \ \ \ \ \ \ \ \ \ \ otherwise \end{matrix}\right.$
其中 $\bar{g_i}^{(t)}=\frac{1}{t}\sum_{r=1}^t g_i^{(t)}$ ，可以看出当某个维度产生的累加梯度平均值的绝对值小于 $\lambda$ ，本维度不重要，权重被置为0，从而解决稀疏化问题。

L1-RDA vs L1-FOBOS

这里对两种方法的公式做进一步的变形，从而很好地比较这两种方法的不同：

L1-FOBOS： $W^{(t+1)}=argmin_W\left \{ G^{(t)}\cdot W + \lambda \left \| W \right \|_1+\frac{1}{2\eta^{(t)}} \left \| W-W^{(t)} \right \|^2_2 \right \}$
L1-RDA： $W^{(t+1)}=argmin_W\left \{ G^{(1:t)}\cdot W + t\lambda \left \| W \right \|_1+\frac{1}{2\eta^{(t)}} \left \| W-0 \right \|_2^2 \right \}$
其中 $G^{(1:t)}=\sum^t_{r=1}G^{(r)}$ ，可以看出L1-FOBOS和L1-RDA的区别为：

对于上述两个公式前两项，前者计算当前梯度和L1正则化项，后者采用累加梯度和L1正则化项，
对于上述两个公式第三项，前者限制 $W$ 不能离当前迭代的 $W^{(t)}$ 太远，后者则只要求不能离0太远。

FTRL

FTRL是综合L1-RDA和L1-FOBOS后提出的算法，公式如下，这里引入L2正则化是为了令结果变得更平滑。
$W^{(t+1)}=argmin_W\left \{ G^{(1:t)}\cdot W + \lambda_1 \left \| W \right \|_1 + \lambda_2 \frac{1}{2} \left \| W \right \|^2_2+\frac{1}{2}\sum_{r=1}^t\sigma^{(r)}\left \| W-W^{(r)} \right \|^2_2\right \}$
经过一套复杂推导公式(此处省略一万个公式)，得到如下结果，
$w_i^{(t+1)}=\left\{\begin{matrix} 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \left | z_i^{(t)}\right |<\lambda_1 \\ -\left ( \lambda_2+\sum_{r=1}^t\sigma^{(r)} \right )^{-1}\left ( z_i^{(t)}-\lambda_1 sgn(z_i^{(t)}) \right ) \ \ \ \ \ otherwise \end{matrix}\right.$
其中 $z_i^{(t)}=g_i^{(1:t)}-\sum_{r=1}^t\sigma^{(r)}w_i^{(r)}$ ，且FTRL中学习率为如下公式，
$\eta_i^{(t)}= \frac{\alpha}{\beta+\sqrt{\sum_{r=1}^t}\left ( g_i^{(r)} \right )^2}$
可以看出，FTRL确实综合了L1-RDA和L1-FOBOS的优点，在实时训练中使用该算法会模型的稀疏性很好，因为它考虑累积权重和累积梯度。

group lasso

在NLP和搜推广领域，输入特征多为embedding，模型对这类特征进行稀疏性处理时，需要在vector-wise层面考虑一组（group）权重参数的置0处理，传统FTRL算法只能在bit-wise层面对权重参数进行处理，因而不能满足需求，因而group lasso优化器应运而生，具体公式如下所示，
$W^{(t+1)}=argmin_W\left \{ G^{(1:t)}\cdot W +\frac{1}{2}\sum_{r=1}^t\sigma^{(r)}\left \| W-W^{(r)} \right \|^2_2 + \Psi(W) \right \}$
其中 $\Psi(W)$ 如下所示，
$\Psi(W)=\sum_{g=1}^G\left ( \lambda_1\left \| W^g \right \|_1+\lambda_{21}\sqrt{d_{W^g}}\left \| A_t^{\frac{1}{2}}W^g \right \|_2 \right )+\lambda_2\left \| W \right \|_2^2$
其中 $G$ 为embedding的个数， $W^g$ 为某个embedding对应的一组权重参数， $d_{W^g}$ 为 $W^g$ 的维度， $\lambda_1$ 为L1正则化系数， $\lambda_{21}$ 为L21正则化系数， $\lambda_{2}$ 为L2正则化系数， $A_t$ 与当前学习率的非线性表示，具体内容可以参见这里，从上面公式看出，group lasso算法对embedding对应权重参数组的稀疏性处理地较好。