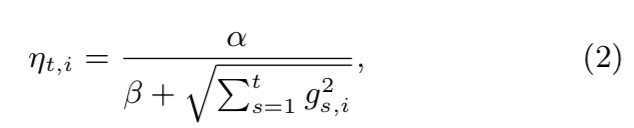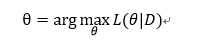以我视角深入理解FTRL模型原理

FTRL算法是吸取了FOBOS算法和RDA算法的优点而衍生而来的算法。

1.FOBOS算法

 

小结：

 2. RDA算法

RDA也叫正则对偶平均算法，特征权重更新如下：

 

小结：

 

3.FTRL算法原理 

 

• 从loss function的形式来看：FTRL就是将RDA-L1的“梯度累加”思想应用在FOBOS-L1上，并施加一个L2正则项。【PS：paper上是没有加L2正则项的】
• 这样达到的效果是：
• • 累积加和限定了新的迭代结果W**不要离“已迭代过的解”太远**；
  • 因为调整后的解不会离迭代过的解太远，所以保证了每次找到让之前所有损失函数之和最小的参数；
  • 保留的RDA-L1中关于累积梯度的项，可以看作是当前特征对损失函数的贡献的一个估计【累积梯度越大，贡献越大。】
  • 由于使用了累积梯度，即使某一次迭代使某个重要特征约束为0，但如果后面这个特征慢慢变得稠密，它的参数又会变为非0；
  • 保留的RDA-L1中关于累积梯度的项，与v相加，总会比原来的v大，加起来的绝对值更容易大于L1的阈值，保护了重要的特征；
• FTRL的巧妙之处在于：
• • 在MSE的前面乘以了一个和learning_rate有着神奇关系的参数σ_s。
  • 因为这个参数，保证了FTRL在不使用L1时和SGD保持了一致性。
• FTRL使用的自适应learning_rate，其思想和 Adagrad Optimizer 类似的自适应思想：
• • 如果特征稀疏，learning_rate就大一点；
  • 如果特征稠密，learning_rate就小一点；
• FTRL中为什么要同时兼顾FOBOS-L1和RDA-L1？？
• • 因为不是为了产出稀疏而进行变化，真正的目的是产出有效的稀疏解。即稀疏又保留有效特征！！！
  • 稀疏靠RDA-L1，保留有效特征靠FOBOS-L1和RDA-L1的累积梯度思想。
• 本质上，FTRL只是一种适用于online-learning的optimizer；
• FTRL-Proximal中的Proximal的含义：
• • t+1次迭代的解，不能离t次迭代的解太远；
  • t+1次迭代的解，不能离0太远；
  • 是对具体约束的表达。