😊😊作者简介😊😊 ： 大家好，我是南瓜籽，一个在校大二学生，我将会持续分享Java相关知识。
🎉🎉个人主页🎉🎉 ： 南瓜籽的主页
✨✨座右铭✨✨ ： 坚持到底，决不放弃，是成功的保证，只要你不放弃，你就有机会，只要放弃的人，他肯定是不会成功的人。

🍎🍎图的基本介绍🍎🍎

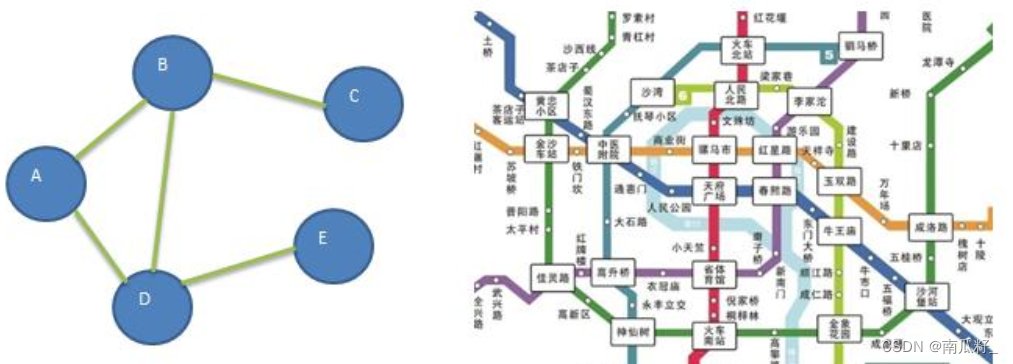
图是一种数据结构，其中结点可以具有零个或多个相邻元素。两个结点之间的连接称为边。结点也可以称为顶点。

🍉🍉图的常用概念🍉🍉

1)顶点(vertex)
2) 边(edge)
3) 路径
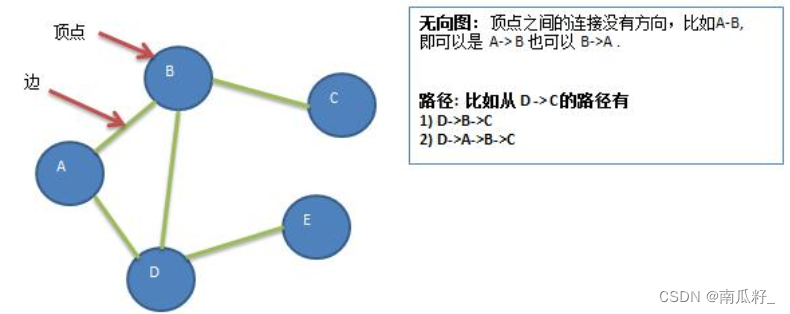
4) 无向图
5) 有向图
6) 带权图

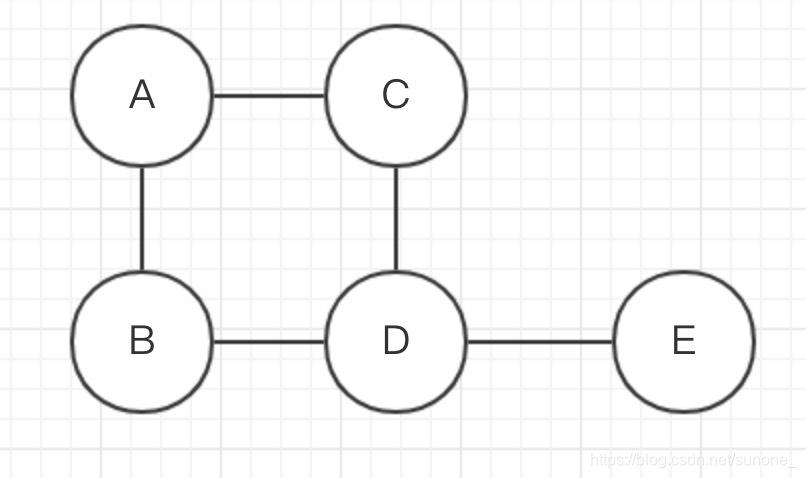
无向图如下:

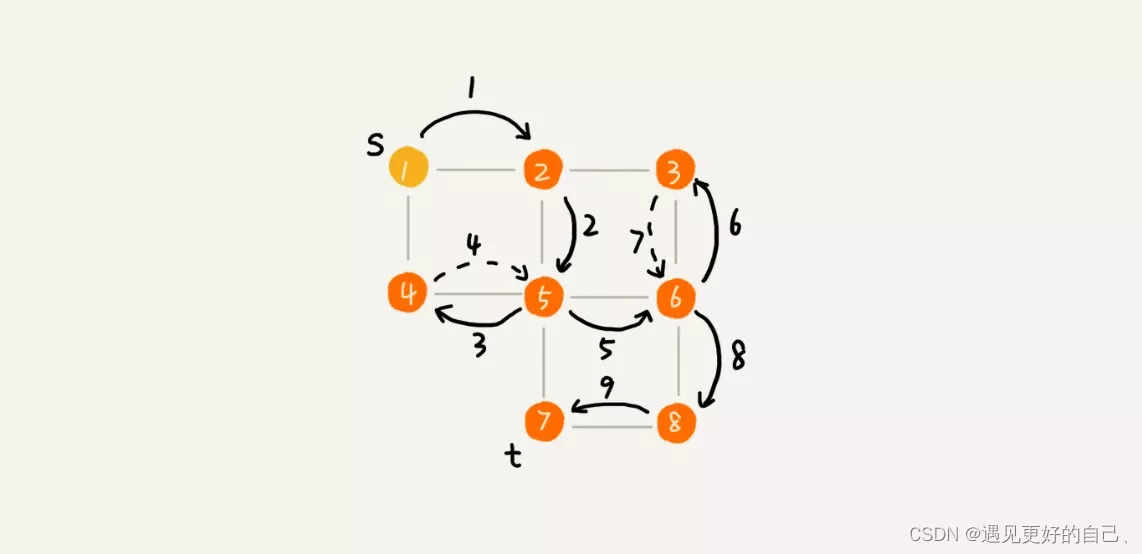
有向图和带权图如下:

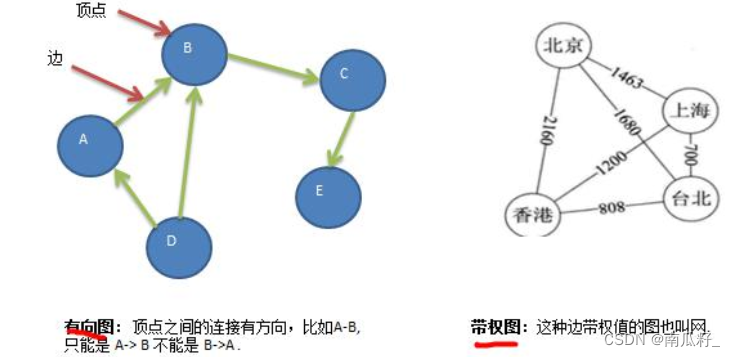
🍒🍒图的表示方式🍒🍒

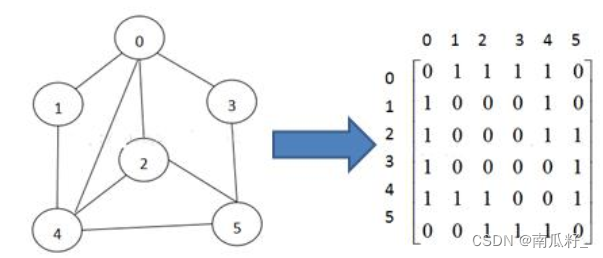
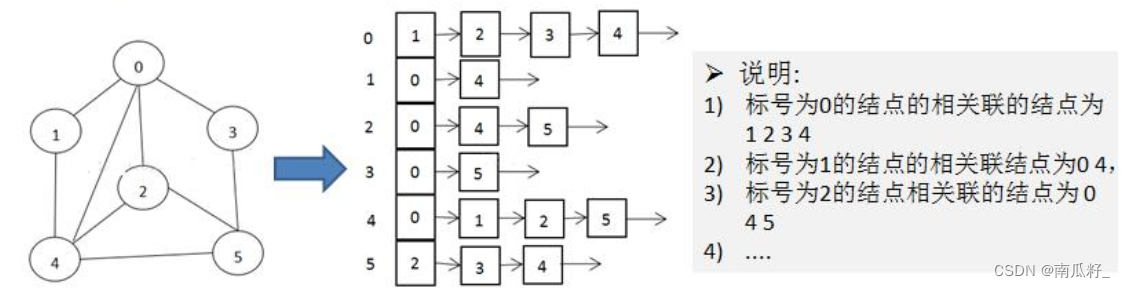
图的表示方式有两种：二维数组表示（邻接矩阵）；链表表示（邻接表）

🍎🍎图的深度优先遍历🍎🍎

🍎🍎深度优先遍历基本思想🍎🍎

图的深度优先搜索(DepthFirstSearch)。

1. 深度优先遍历，从初始访问结点出发，初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点，可以这样理解：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。
2. 我们可以看到，这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。
3. 显然，深度优先搜索是一个递归的过程

🍎🍎深度优先遍历算法步骤🍎🍎

1. 访问初始结点v，并标记结点v为已访问。
2. 查找结点v的第一个邻接结点w。
3. 若w存在，则继续执行4，如果w不存在，则回到第1步，将从v的下一个结点继续。
4. 若w未被访问，对w进行深度优先遍历递归（即把w当做另一个v，然后进行步骤123）。
5. 查找结点v的w邻接结点的下一个邻接结点，转到步骤3。

🍎🍎深度优先算法代码实现🍎🍎

/*** 深度优先遍历* @param isVisited* @param i*/public void dfs(boolean[] isVisited,int i){// 1.输出节点System.out.print(getVertex(i)  + "->");// 2.将该节点设置为已访问isVisited[i] = true;// 3.找到该节点下一个邻接节点的下标int w = getFirstNeighbor(i);while (w != -1){ // 说明有下一个邻接节点if (!isVisited[w]){// 如果该节点没有被访问dfs(isVisited,w);}else {// 如果该节点被访问过w = getNextNeighbor(i,w);}}}/*** 方法重载，遍历所有节点，并进行dfs*/public void dfs(){for (int i = 0; i < getNumOfVertex(); i++) {if (!isVisited[i]){// 没有被访问过的节点dfs(isVisited,i);}}}

🍉🍉图的广度优先遍历🍉🍉

🍉🍉广度优先遍历基本思想🍉🍉

1. 图的广度优先搜索(BroadFirstSearch)。
2. 类似于一个分层搜索的过程，广度优先遍历需要使用一个队列以保持访问过的结点的顺序，以便按这个顺序来访问这些结点的邻接结点

🍉🍉广度优先遍历算法步骤🍉🍉

1. 访问初始结点v并标记结点v为已访问。
2. 结点v入队列。
3. 当队列非空时，继续执行，否则算法结束。
4. 出队列，取得队头结点top。
5. 查找结点top的第一个邻接结点next。
6. 若结点top的邻接结点next不存在，则转到步骤3；否则循环执行以下三个步骤：
   6.1若结点next尚未被访问，则访问结点next并标记为已访问。
   6.2结点next入队列
   6.3查找结点top的继next邻接结点后的下一个邻接结点next，转到步骤6。

🍉🍉广度优先算法代码实现🍉🍉

    /*** 对一个节点进行广度优先遍历*/public void bfs(boolean[] isVisited,int i){int top; // 头节点下标int next; // 邻接节点下标// 1.输出该节点System.out.print(getVertex(i) + "->");// 2.将当前节点标志为已访问isVisited[i] = true;// 3.节点入队列Queue queue = new Queue(vertexList.size());queue.inQueue(i);// 4.遍历队列while (!queue.isEmpty()){// 4.1取出队头节点下标top = queue.outQueue();// 4.2得到第一个邻接节点的下标next = getFirstNeighbor(top);while (next != -1){// 4.3找到了第一个邻接节点的下标if (!isVisited[next]){// 4.3.1没有被访问过，输出该节点System.out.print(getVertex(next) + "->");// 4.3.2将该节点标志为已访问isVisited[next] = true;// 4.3.3节点入队列queue.inQueue(next);}else {// 4.4如果已经访问过了,得到下一个邻接节点的下标next = getNextNeighbor(top,next); // 广度优先}}}}/*** 方法重载，对所有节点进行广度优先遍历*/public void bfs(){for (int i = 0; i < getNumOfVertex(); i++) {if (!isVisited[i]){bfs(isVisited,i);}}}

🍒🍒图的属性和其他方法定义🍒🍒

public class Graph {private List<String> vertexList; // 存储顶点集合private int[][] edges;// 存储图对应的邻接矩阵private int numOfEdges; // 表示边的数目private boolean[] isVisited; // 记录某个顶点是否被访问过/*** 构造器初始化* @param n*/public Graph(int n) {this.vertexList = new ArrayList<>(n);this.edges = new int[n][n];this.isVisited = new boolean[n];this.numOfEdges = 0;}/**** @param index* @return 得到第一个邻接节点的下标*/public int getFirstNeighbor(int index){for (int i = 0; i < vertexList.size(); i++) {if (edges[index][i] > 0){return i;}}return -1;}/*** 根据前一个邻接节点下标找到下一个邻接节点* @param v1* @param v2* @return 找到了返回下标，否则返回 -1*/public int getNextNeighbor(int v1,int v2){for (int i = v2 + 1; i < vertexList.size(); i++) {if (edges[v1][i] > 0){return i;}}return -1;}/**** @return 得到图中节点的个数*/public int getNumOfVertex(){return vertexList.size();}/**** @return 得到边的个数*/public int getNumOfEdges(){return numOfEdges;}/**** @param index 下标* @return 返回节点对应的值*/public String getVertex(int index){return vertexList.get(index);}/**** @param v1* @param v2* @return 返回v1和v2对应的权值*/public int getWeight(int v1,int v2){return edges[v1][v2];}/*** 插入节点* @param vertex*/public void insertVertex(String vertex){vertexList.add(vertex);}/*** 插入边* @param v1 点的下标* @param v2 点的下标* @param weight 权值*/public void insertEdge(int v1,int v2,int weight){// 无向图，需要两边都存储edges[v1][v2] = weight;edges[v2][v1] = weight;numOfEdges++;// 边的数目增加}/*** 显示图对应的矩阵*/public void showGraph(){for (int[] edge : edges) {System.out.println(Arrays.toString(edge));}}
}

🍒🍒队列🍒🍒

class Queue {private int maxSize; // 数组的最大容量private int front;// 队列头private int rear;// 队列尾private int[] arr;// 该数组用于存放数据, 模拟队列public Queue(int maxSize){// 初始化队列this.maxSize = maxSize;this.front = -1;// 指向队列头部this.rear = -1;// 指向队列尾部arr = new int[maxSize];// 初始化数组}/*** 判断队列是否已满* @return true 为满  false为未满*/public boolean isFull(){return this.rear == this.maxSize - 1;}/*** 判断队列是否为空* @return  true为空  false已经有了数据*/public boolean isEmpty(){return this.rear == this.front;}/*** 添加数据到队列中* @param n*/public void inQueue(int n){// 1.判断队列是否已满if (isFull()){System.out.printf("队列已满,%d无法存入队列中\n",n);return;}this.rear++;this.arr[rear] = n;}/*** 出队列* @return*/public int outQueue(){// 1.判断是否为空if (isEmpty()){throw new RuntimeException("队列为空,不能出队列");}this.front++;// 返回数据return this.arr[front];}/*** 显示队列所有数据*/public void listQueue(){// 1.判断是否为空if (isEmpty()){throw new RuntimeException("队列为空");}System.out.println("--------队列数据显示-------");for (int i = 0; i < arr.length; i++) {System.out.printf("arr[%d]=%d\n",i,arr[i]);}System.out.println();}/*** 得到队头数据* @return*/public int getHeadQueue(){// 1.判断是否为空if (isEmpty()){throw new RuntimeException("队列为空~~~");}// 2.返回return this.arr[this.front + 1];}
}

🎉🎉测试🎉🎉

    public static void main(String[] args) {// 初始化图和邻接矩阵Graph graph = new Graph(5);graph.insertVertex("A");graph.insertVertex("B");graph.insertVertex("C");graph.insertVertex("D");graph.insertVertex("E");graph.insertEdge(0,1,1);graph.insertEdge(0,2,1);graph.insertEdge(1,2,1);graph.insertEdge(1,3,1);graph.insertEdge(1,4,1);// 图的遍历graph.showGraph();// 深度优先遍历System.out.println("------------深度优先遍历");graph.dfs();// 广度优先遍历System.out.println("------------广度优先遍历");graph.bfs();}

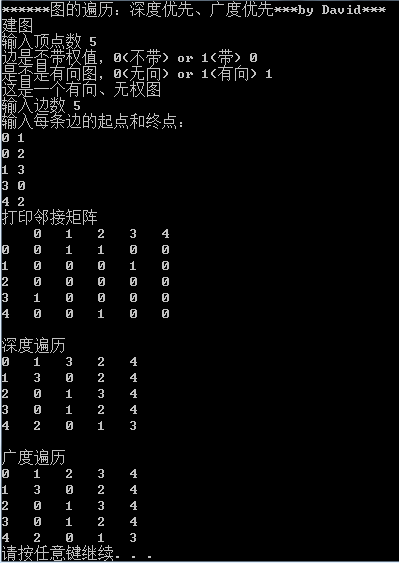
结果:

[0, 1, 1, 0, 0]
[1, 0, 1, 1, 1]
[1, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
[0, 1, 0, 0, 0]
------------深度优先遍历
A->B->C->D->E->
------------广度优先遍历
A->B->C->D->E->