为什么要归一化？

归一化已成为深度神经网络中的一个重要步骤，它可以弥补ReLU、ELU等激活函数无界性的问题。有了这些激活函数，输出层就不会被限制在一个有限的范围内(比如tanh的 $[- 1, 1]$ )，而是可以根据训练需要尽可能高地增长。为了限制无界激活函数使其不增加输出层的值，需要在激活函数之前进行归一化。在深度神经网络中有两种常用的归一化技术，但常被初学者所误解。在本教程中，将详细解释这两种归一化技术，以突出它们的关键区别。

局部响应归一化（Local Response Normalization，LRN）

局部响应归一化（LRN）最初是在AlexNet架构中引入的，其中使用的激活函数是ReLU，而不是当时更常见的tanh和sigmoid。除了上述原因，使用LRN的原因是为了鼓励横向抑制（lateral inhibition）。这是神经生物学中的一个概念，是指神经元减少其邻居活动的能力[1]（注：阻止兴奋神经元向邻近神经元传播其动作趋势，从而减少兴奋神经元的邻近神经元的激活程度）。在深度神经网络（Deep Neural Networks，DNN）中，这种横向抑制的目的是进行局部对比度增强，以便使局部最大像素值用作下一层的激励。

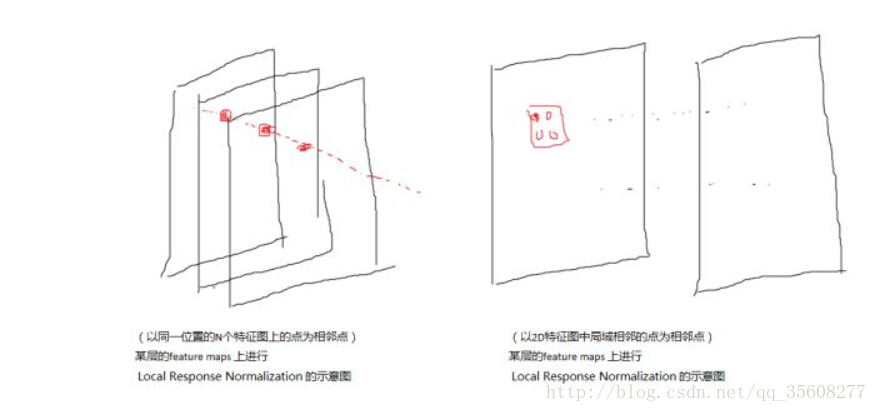
LRN是一个不可训练的层，用于对局部邻域内的特征图中的像素值进行平方归一化。根据所定义的邻域，有两种类型的LRN，如下图所示：

在这里插入图片描述

通道间的LRN（Inter-Channel LRN）：这最早是在AlexNet论文中使用的。定义的邻域在整个通道上，对于每个(x,y)位置，在深度维度上进行归一化，其公式如下：

其中， $i$ 表示滤波器 $i$ 的输出， $a (x, y)$ 、 $b (x, y)$ 分别为归一化前后 $(x, y)$ 处的像素值，N为通道总数。常数 $(k,\alpha,\beta,n)$ 为超参数。k用于避免奇异点(分母为零的情况)， $\alpha$ 为归一化常数， $\beta$ 是对比度常数。常数 $n$ 用于定义邻域长度，即在进行归一化时需要考虑多少个连续像素值。 $(k,\alpha,\beta,n)=(0, 1, 1, n)$ 的情况是标准归一化。在上图中，N=4，n=2。

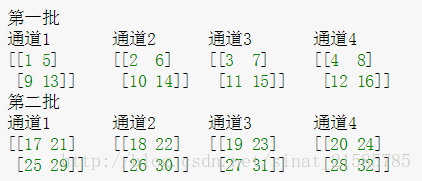
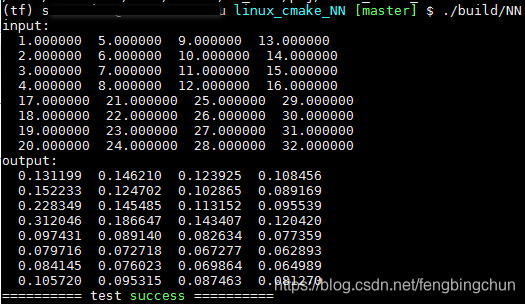
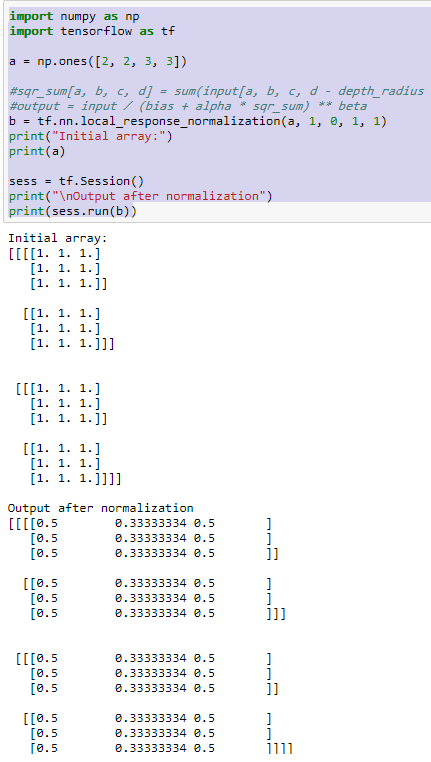
让我们来看一个通道间LRN的例子。如下图：
在这里插入图片描述
不同的颜色表示不同的通道，因此N=4。设置超参数为 $(k,\alpha,\beta,n)=(0,1,1,2)$ 。n=2的值表示在计算位置 $(i, x, y)$ 处的归一化值时，我们考虑上一个滤波器和下一个滤波器在相同位置的值，即 $(i - 1, x, y)$ 和 $(i + 1, x, y)$ 。对于 $(i, x, y) = (0, 0, 0)$ （此处表示位置），我们有值 $(i, x, y) = 1$ ，值 $(i - 1, x, y)$ 不存在，值 $(i + 1, x, y) = 1$ 。因此 $normalized\_value(i (x, y)=\frac{1}{1^2+1^2}=0.5$ ,可以在上图的下部看到。其余归一化值的计算方法类似。

通道内的LRN（Intra-Channel LRN）：由上面的图可以看到，在通道内LRN中，邻域仅在同一通道中扩展。公式为：

其中(W,H)为特征图的宽和高（如上面第一幅图中 $(W, H) = (8, 8)$ ）。通道间LRN和通道内LRN之间的惟一区别是归一化的邻域。在通道内LRN中，一个二维邻域（相对于通道间的一维邻域）是在考虑的像素周围定义的。例如，下图显示了在 $n = 2$ 的5x5特征图上的通道内归一化（即以 $(x, y)$ 为中心的大小为 $(n+1)\times(n+1)$ 的2D邻域)。

在这里插入图片描述

批量归一化（Batch Normalization，BN）

批量归一化（BN）是一个可训练的层，通常用于解决内部协变量偏移（Internal Covariate Shift，ICS）[1]的问题。ICS的出现是由于隐藏的神经元或激活的分布发生了变化。考虑下面的二元分类示例，其中我们需要对有玫瑰和无玫瑰进行分类：
在这里插入图片描述

假设我们已经训练了一个神经网络，现在我们从数据集中选择两个明显不同的batch进行推断（如上所示）。如果我们对这两个batch进行前向传播，并绘制隐藏层（在网络深处）的特征空间，我们将看到分布的显著变化，如图右侧所示。这叫做输入神经元的协变量偏移。这对训练有什么影响?在训练过程中，如果我们选择属于不同分布的batch，那么它会减慢训练速度，因为对于给定的batch，它会尝试学习某个特定的分布，而对于下一个batch则有所不同。因此它会在分布之间来回跳动直到收敛。通过确保batch中的成员不属于相同或相似的分布，可以缓解这种协变量偏移。这可以通过随机选择batch图像来实现。对于隐藏神经元，也存在类似的协变量偏移。即使这些batch是随机选择的，隐藏的神经元也可能最终具有一定的分布，从而减慢了训练的速度。隐藏层的这种协变量偏移称为内部协变量偏移。问题是我们不能像控制输入神经元那样直接控制隐藏神经元的分布，因为随着训练更新训练参数，它会不断变化。批量归一化有助于缓解这个问题。

在批量归一化中，隐藏神经元的输出按如下方式处理，然后输入激活函数：

将整个batch B归一化为零均值和单位方差：
- 计算整个mini-batch输出的平均值： $u\_B$
- 计算整个mini-batch输出的方差： $sigma\_B$
- 通过减去平均值并除以方差来归一化mini-batch
引入两个可训练的参数（Gamma：尺度变量和Beta：平移变量）以缩放和移动归一化的mini-batch输出；
将此缩放并移动的归一化mini-batch输入激活函数。

BN算法如下图所示：
在这里插入图片描述

对batch中所有激活中的每个像素进行归一化。考虑下图。让我们假设我们有一个大小为3的mini-batch。一个隐藏层产生一个大小为 $(C, H, W) = (4, 4, 4)$ 的激活。由于batch-size为3，我们将有3个这样的激活。现在，对于激活中的每个像素（即对于每个4x4x4=64像素），我们将通过找到所有激活中的这个像素位置的平均值和方差对其进行归一化，如下图的左侧所示。一旦找到平均值和方差，我们将从每个激活中减去平均值并将其除以方差。下图的右侧部分对此进行了描述。减法和除法是逐点进行的。

在这里插入图片描述

第2步（即缩放和平移）的原因是为了让训练来决定我们是否需要归一化。在某些情况下，不进行归一化可能会产生更好的结果。因此，BN让训练来决定是否包含归一化层，而不是事先就设定好。当 $Gamma=sigma\_B$ 且 $Beta=u\_B$ 时，不执行任何归一化操作，并且恢复原始激活。在这里可以找到Andrew Ng提供的关于BN的非常好的视频教程。

对比

LRN有多个方向来（内部或内部通道）执行归一化，另一方面，BN只有一种执行方式（针对所有激活中的每个像素位置）。下表比较了这两种归一化技术。
在这里插入图片描述

参考：

[1] https://www.learnopencv.com/batch-normalization-in-deep-networks/
[2] Ioffe, Sergey, and Christian Szegedy. “Batch normalization: Accelerating deep network training by reducing internal covariate shift.” arXiv preprint arXiv:1502.03167 (2015).