这篇博客要介绍的是算术编码、译码。主要用分组编码的思路解决了当消息比较长时，小数位数太多，计算工具精度达不到的问题。 文末给出了matlab代码。题目的要求是：已知26个英文字母和空格的统计概率，对文本文档中的消息（很长的消息，比如一篇英文小作文）进行算术编码译码。概率分布如下：

首先简单介绍下算术和编码：算术编码是数据压缩的主要算法之一。 是一种无损数据压缩方法，也是一种熵编码的方法。和其它熵编码方法不同的地方在于，其他的熵编码方法通常是把输入的消息分割为符号，然后对每个符号进行编码，而算术编码是直接把整个输入的消息编码为一个数，一个满足(0.0 ≤ n < 1.0)的小数n。

编码译码流程：

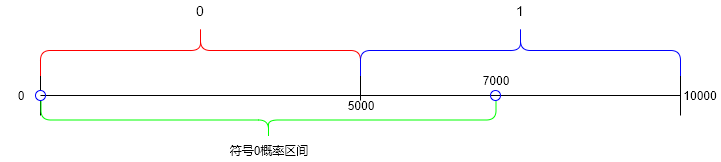
1）首先，按照各信源符号的概率分布，将[0, 1)这个区间分成若干个子区间，那么每个符号就会有自己对应的区间；
2）将[0, 1)这个区间设置为初始间隔，读入一个符号读入，判断该符号落入哪一区间。然后将该区间按照[0, 1)上区间划分等比例的划分出新的子区间，等待下一个符号的落入；
3）然后依次迭代，不断重复进行步骤2，直到最后信源符号全部读完为止。

译码的前提是已知信源符号的概率分布。译码的过程为：
1）根据信源符号的概率分布，将[0, 1)这个区间分成若干个子区间，每个子区间对应一个信源符号；
2）读入编码结果，判断编码结果落在哪一子区间，对应符号即为该为译码结果。然后将该区间按照[0, 1)上区间划分等比例的划分出新的子区间，等待下一次比较；
3）然后依次迭代，不断重复进行步骤2，直到译出全部的符号。

下面以一个简单的例子来说明算术编码译码的流程。

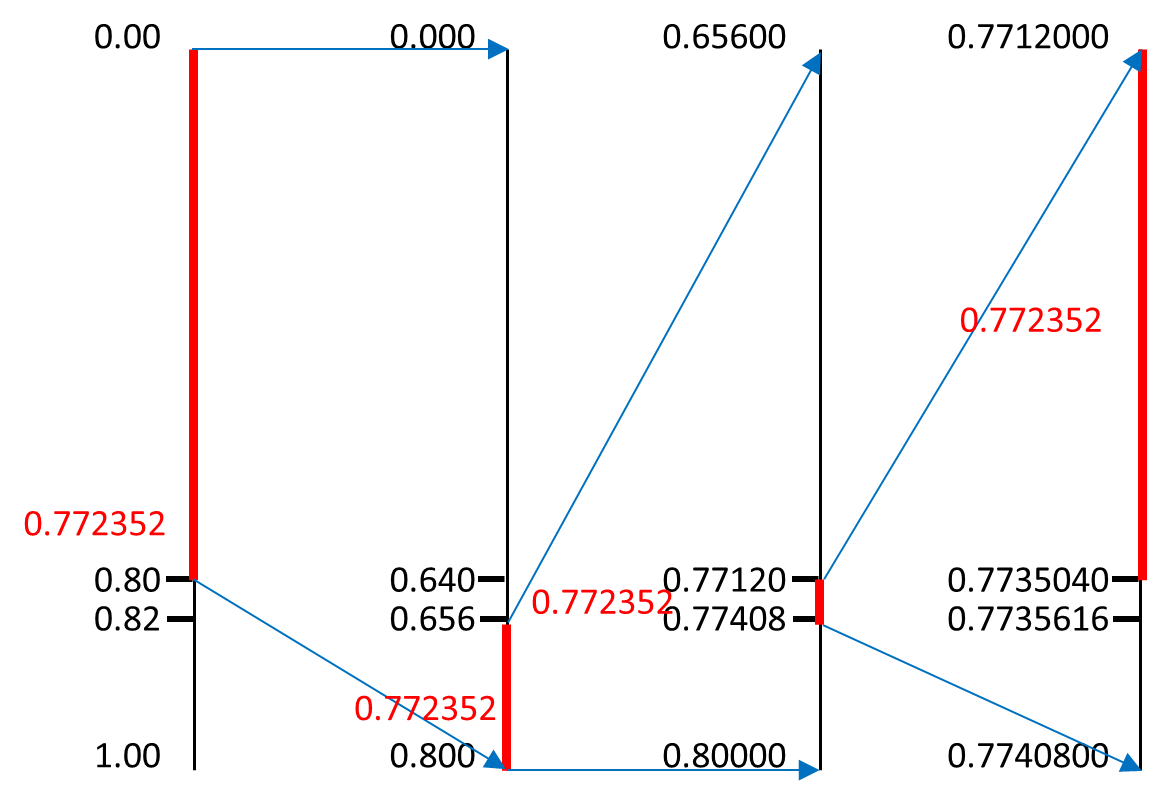
设信源符号以及概率分布为{A:0.4,B:0.4,C:0.2}，要编码的消息为‘ACB’根据概率分布对[0,1]划分，可以画出概率轴，可以看到概率轴上，ABC分别对应各自区间。每一次编码都要确定一次概率区间。首先第一个符号A确定了区间为[0,0.4],然后对[0,0.4]按照符号的概率分布再次划分，画出第二个概率轴，第二个符号C对应的区间为[0.32,0.4]，再对[0.32,0.4]按照符号的概率分布再次划分，画出第三个概率轴，第三个符号B对应的区间为[0.352,0.384]，到这里，编码结束，如果是更长的消息，那么以此类推。最终区间为[0.352,0.384]，我们取中点0.368，将其转化为二进制数，就是算术编码的结果，可以对这个二进制数进行接下来的信道编码、调制等等操作。

译码时同样先把二进制转换为小数，生成概率轴，不断的判断小数位于哪一个区间，以确定对应哪一个字母，直到译出全部字母。
**

算术编码的性能分析

**
算术编码与霍夫曼编码都是熵编码，即概率越小的字符，用更多的bit去表示，这反映到概率区间上就是，概率小的字符所对应的区间也小，因此这个区间的上下边际值的差值越小，为了唯一确定当前这个区间，则需要更多的数字去表示它。对于霍夫曼编码，每个信源符号都有准确且唯一的码字与之对应，但是由于位数只能取整数，所以每个信源符号的位数与它的概率并不是严格的线性关系，而是有一定的近似。对于算术编码，每个符号并没有准确唯一的码字与之对应，根据编码流程知道一条完整的信源消息会对应一个编码结果，如果按照霍夫曼编码的思想考虑码字与符号的对应关系，会发现不同码字的符号之间的界限并不是明确的，而是有重叠的，这从一个角度解释了算术编码可以比霍夫曼编码更加逼近香农极限。

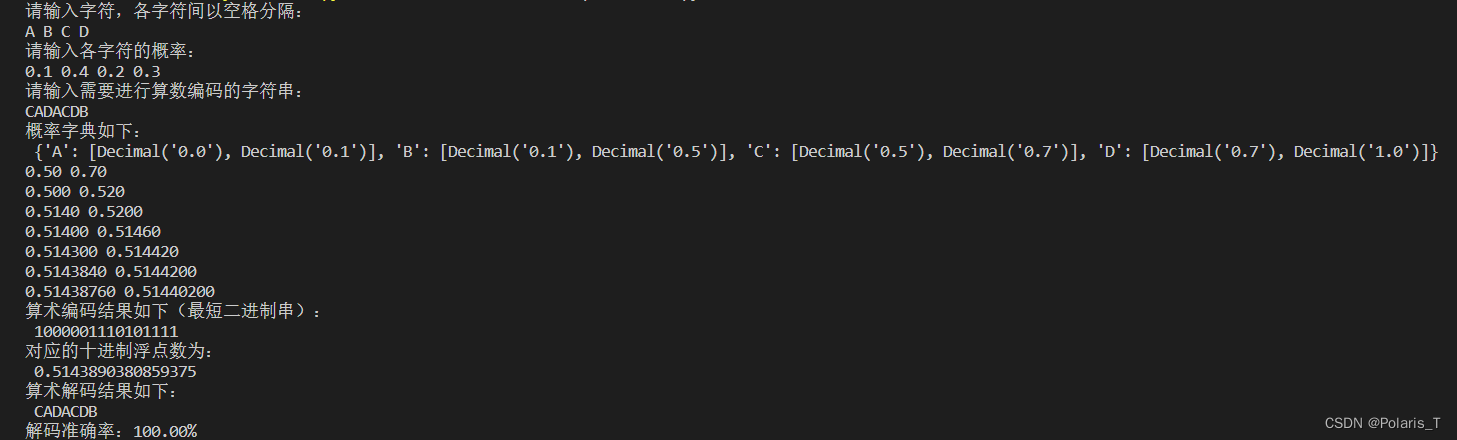
但是算术编码存在的一个问题就是，当一条消息很长时，理论上编码结果的小数的精度就越高，当超过了运行环境的计算精度时，会发生精度溢出，造成编码失败。在仿真过程中，我们就碰到了这样的问题，提供一个简单的解决思路，那就是分组编码。在编码前确定对每组多少个字母进行编码，不会出现精度问题，比如我在代码中将每组字母数设置为5，将一个很长的信息，等分成若干组，对每一组分别进行算术编码，译码时也是对每一组分别进行译码。那么在代码实现中，在对每一组编码完成以后，在二进制序列后面加了一个空格作为标识符，用来隔开不同组的编码结果。在译码时，不断的读取编码序列，每读到一个空格，就对读到的序列进行译码，这是一组的译码结果。不断的重复这个过程，直到序列都被译码成消息。

**

代码实现

**
这道题关键在于要传递的消息很长，一口气编完显然是不可能的，小数点后面不知多少位了，那么就需要用分组编码的思想。做作业的过程中，没有找到很合适的参考代码，于是自己试着写了下，有些地方可能不是很合适，欢迎大家和我交流~
主程序很简单，只有简单的几行，然后主要的几个函数，编码函数、译码函数、码长计算函数、十进制小数转二进制函数和二进制转十进制小数函数，可能需要仔细看一看。要想成功运行程序，首先要自己建立一个send.txt，里面存要编码的消息，注意，不要有标点。

clc
sym=['a' 'b' 'c' 'd' 'e' 'f' 'g' 'h' 'i' 'j' 'k' 'l' 'm' 'n' 'o' 'p' 'q' 'r' 's' 't' 'u' 'v' 'w' 'x' 'y' 'z' ' ' ];
p=[0.0575 0.0128 0.0263 0.0285 0.0913 0.0173 0.0133 0.0313 0.0599 0.0006 0.0084 0.0335 0.0235 0.0596 0.0689 0.0192 0.0008 0.0508 0.0567 0.0706 0.0334 0.0069 0.0119 0.0073 0.0164 0.0007 0.1928];
allmessage=fileread('send.txt');%从send.txt中读取消息 
allmessage=lower(allmessage);%把大写字母变成小写  
allmessage=regexprep(allmessage,{','},' ');%去掉逗号，如果其它标点，请去掉 
code1= arithCode(allmessage,sym,p,5);%编码，每次编5个字母 
decode1=arithDecode(code1,sym,p,5);%译码 
fid=fopen('result.txt','w');%把译码结果存入result.txt中 
fprintf(fid,'%s',decode1);
fclose(fid);%以下是用到的函数和具体的说明  
%编码函数
function [ codeBin ] = arithCode( message,alphaDic,alphaProb,symNum)
%对输入的消息序列进行算术编码 
%  codeBin 输出的二进制编码序列 
%  message  输入的消息序列  
%  alphaDic  信源符号集合 
%  alphaProb  信源符号对应的概率
%  symNum    进行一次算术编码对多少个符号进行编码
probValOri(1)=0;%字母a对应的区间起点是0 
for i=1:length(alphaDic)probValOri(i+1)=probValOri(i)+alphaProb(i);%把字母按照概率分布对应给[0,1]上的不同概率区间，生成概率轴
end
totalLen=length(message);%要编码的消息的长度 
operaNum=floor(totalLen/symNum);%商是整数，为编码次数；非整数，则为编码次数-1 
restSymNum=mod(totalLen,symNum);%最后一次算术编码要处理的字母个数 
codeBin=[];%编码后的二进制序列  
%按照次数遍历 
for k=0:operaNum-1left=0;%区间左界 valLen=1;%区间长度  probVal=probValOri;shortMes=message(k*symNum+1:(k+1)*symNum);%每次处理symNum个字母 %每一次对symNum个字母的编码流程如下 for i=1:symNumleft=left+probVal(find(alphaDic==shortMes(i)));%确定第i个字母在概率轴的位置，左界 right=left+alphaProb(find(alphaDic==shortMes(i)))*valLen;%左界加这个字母对应的概率为右界 %每进行一次编码，原始概率分布都要乘以区间长度进行缩小valLen=right-left;probVal=probValOri*valLen;%概率轴也要按照区间长度缩小，为下一个字母编码准备endmiddle=0.5*(right+left)%编好的小数 codeLen=calcCodeLen(alphaProb,alphaDic,shortMes);%计算编码长度 shortCodeBin=deciConvertBin(middle,2*codeLen);%将小数转换成指定长度的二进制序列 shortCodeBin=[shortCodeBin ' '];%每一次编码完成后，末尾加空格，隔开下一次的序列  codeBin=[codeBin shortCodeBin];%将编码序列存入 shortCodeBin=[];
end
%如果商不为0，对最后剩下的字母进行编码，和上面的流程类似
if(restSymNum~=0)left=0;valLen=1;probVal=probValOri;for j=totalLen-restSymNum+1:totalLenleft=left+probVal(find(alphaDic==message(j)));right=left+alphaProb(find(alphaDic==message(j)))*valLen;valLen=right-left;probVal=probValOri.*valLen;endmiddle=0.5*(right+left); codeLen=calcCodeLen(alphaProb,alphaDic,message(totalLen-restSymNum+1:totalLen));shortCodeBin=deciConvertBin(middle,2*codeLen);shortCodeBin=[shortCodeBin ' '];codeBin=[codeBin shortCodeBin];
end
end%译码函数
function [ mesDecode] = arithDecode(codeBin,alphaDic,alphaProb,symNum )
%  对编好的二进制序列进行算术译码 
%  codeBin是编好的二进制序列  
%  alphaDic  信源符号集合 
%  alphaProb  信源符号对应的概率 
%  mesDecode  输出的译码消息 
%  symNum    进行一次算术编码对多少个符号进行编码
shortMes=[];mesDecode=[];shortCodeBin=[];%一次译码所得消息、全部消息、一次译码要处理的二进制序列
%每检测到一次空格，就停止向shortCodeBin中读入数字，对已经读入的二进制序列译码
for i=1:length(codeBin)if(codeBin(i)~=' ')shortCodeBin=[shortCodeBin codeBin(i)];elsecodeDec=deciConvertDec(shortCodeBin);%把二进制序列转化为十进制小数 probValOri(1)=0;%按照字母的概率分布，生成概率轴 for j=1:length(alphaDic)probValOri(j+1)=probValOri(j)+alphaProb(j);endleft=0;val=1;probVal=probValOri;%已知一次编译码处理symNum个字母  for k=1:symNum%通过判断codeDec位于概率轴的哪个区间，判断字母是什么 for m=1:length(alphaDic)if(codeDec>=left+probVal(m)&&codeDec<=left+probVal(m+1))shortMes=[shortMes alphaDic(m)];break;endend%每译码一个字母，更新区间长度、左界和概率轴val=probVal(m+1)-probVal(m);left=left+probVal(m);probVal=probValOri.*val;    endmesDecode=[mesDecode shortMes];shortMes=[];shortCodeBin=[];end
end
end%计算消息码长
function [ codeLen ] = calcCodeLen(prob,alpha,message)
%计算码长，根据信息论，计算一个字符串的信息量，单位为bit 
multiProb=1;
for i=1:length(message)multiProb=multiProb*prob(find(alpha==message(i)));
end
codeLen=ceil(-log2(multiProb));
end%十进制小数转二进制
function [ bin ] = deciConvertBin( deci,codeLen )
%将十进制小数转化为规定长度的二进制序列  
%这段代码有一个bug，就是没有考虑当bin全是1时的进位  
bins=[];
for i=1:codeLendeci=2*deci;inte=floor(deci);deci=deci-inte;inteStr=num2str(inte);bins=[bins inteStr];
end
for j=codeLen:-1:1if(bins(j)=='0')bins(j)='1';break;elsebins(j)='0';end
end 
bin=bins;
end%二进制序列转十进制小数
function [ dec ] = deciConvertDec(bin )
%二进制小数转化成十进制小数（0、1之间）
%Convert binary decimals to decimal decimals (between 0 and 1)
bins=[];
for j=1:length(bin)bins(j)=str2num(bin(j));
end
dec=0;
for i=1:length(bins)dec=dec+2.^(-i)*bins(i);
end
end