前言
-
什么是装饰器
-
实现原理
-
实现效果
-
适用场景
装饰器:
-
装饰器的写法
-
装饰器的拓展
-
装饰器的模板
-
什么是装饰器呢?
就是在特定条件下为某些函数再不改动函数体的时候为函数新添加一些功能,这就是装饰器
-
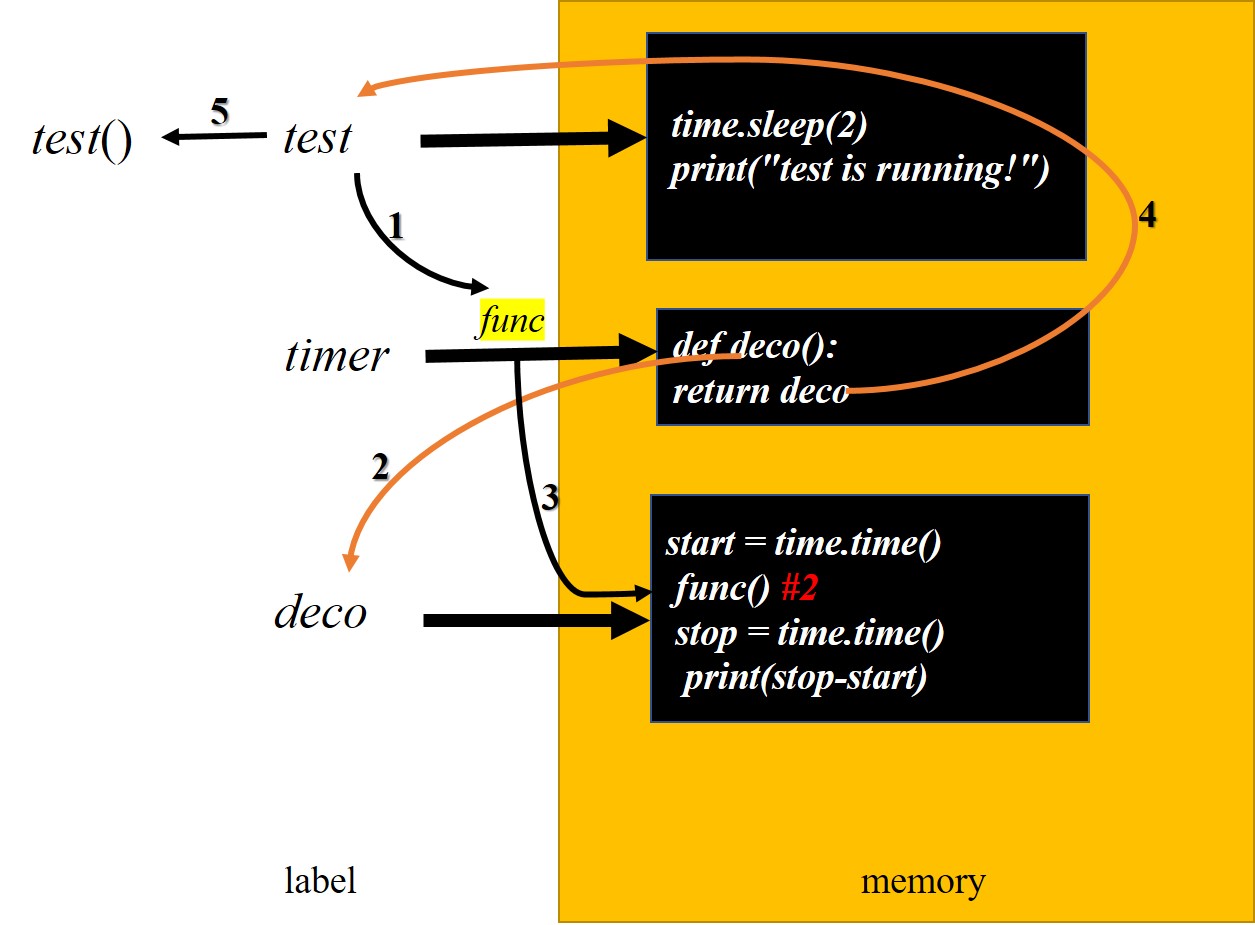
实现原理:
基于@语法和函数闭包,将原函数封装在闭包中,然后将函数赋值为一个新的函数(内置函数),执行函数时再在内层函数中执行闭包中的原函数
-
实现效果:
可以在你改变函数内部代码和调用的前提下,实现在函数执行和执行拓展功能
-
适用场景:
多个函数系统统一在执行前后定义一些功能
关于前言我们了解这么多就够了,然后小编带着大家推导出装饰器
装饰器:
-
装饰器的写法:
这里我们有一个需求,我们定义了5个函数,想在5个函数执行前和执行后都打印一句话:装饰器的学习。首先我们来写于一下没有装饰器的写法,话不多说直接上代码:
def a():passdef b():passdef c():passdef d():passdef e():pass先定义5个函数,再加上我们要打印的话:
def a():print("装饰器的学习")print("装饰器的学习")def b():print("装饰器的学习")print("装饰器的学习")def c():print("装饰器的学习")print("装饰器的学习")def d():print("装饰器的学习")print("装饰器的学习")def e():print("装饰器的学习")passprint("装饰器的学习")a()
b()
c()
d()
e()运行一下:

发现运行成功,但我们想如果我要修改打印的话就要都修改一次,特别麻烦,而且,这是5个函数如果是500个,我们还要一个一个的去加吗?这就有我们的装饰器了,首先我用装饰器修改下,再给大家解释。
def outer(origin):def inner():print("装饰器的学习")res = origin()print("装饰器的学习")return resreturn inner@outer
def a():pass@outer
def b():pass@outer
def c():pass@outer
def d():pass@outer
def e():passa()
b()
c()
d()
e()
运行一下:

发现这样我们也成功了,接下来小编来个大家解释
- 首先:
我们要明白@的作用,那我们的函数a来举例子@的作用就是帮我们执行一次a=outer(a),首先python将把我们的a变成参数传给outer函数,运行后再赋值给a,这就是@的作用。
- 其次给大家解释一下自定的outer函数
我自己称这个函数为@下函数的补丁函数,也就是装饰器函数还是拿a函数举例子,首先a函数变成参数传给了我们的outer函数,outer里又嵌套了一个inner函数 ,然后将函数a赋值给res,然后用return语句返回出结果,外层函数返回inner函数,也就是将inner函数运行一次,这就是工作流程。
- 最后分别在各函数前加上装饰,最后运行出结果

这就是装饰器的写法。
- 装饰器的参数
这时我遇到一个问题如果函数内有参数而且每个函数的参数数量不同,我们应该怎末办,先看下面代码
def outer(origin):def inner():print("装饰器的学习")res = origin()print("装饰器的学习")return resreturn inner@outer
def a(g, e):pass@outer
def b(w):pass@outer
def c(u, y, t):pass@outer
def d(c):pass@outer
def e():passa()
b()
c()
d()
e()这时我们运行一下

发现报错,是因为我们的装饰器内没有这两个参数,那可以在装饰器内设置两个参数,但问题是,有的函数内有3个参数,而有的函数内没有参数,那我们应该怎么办?
针对这个问题我们可以给装饰器设置动态参数,先看代码:
def outer(origin):def inner(*args, **kwargs):print("装饰器的学习")res = origin(*args, **kwargs)print("装饰器的学习")return resreturn inner@outer
def a(a1):print("我是一函数")@outer
def b(a1, a2):print("我是二函数")@outer
def c(a5, a6, a7):print("我是三函数")a(1)
b(2, 3)
c(4, 5, 6)因为函数太多了,小编有点麻烦就剪了几个函数,但道理是相同的,这时我们再运行一下

这样我们就成功了,以上就是装饰器的写法,接下来给大家拓展一下
-
装饰器的拓展:(functools模块)
首先给大家引入一下这时教给大家几个魔法方法
| .__name__ | 获取函数名字 |
| .__doc__ | 获取函数内的注释 |
接下来我们实战一下
def outer(origin):def inner(*args, **kwargs):# 我是一个装饰器函数print("装饰器的学习")res = origin(*args, **kwargs)print("装饰器的学习")return resreturn inner@outer
def c(a5, a6, a7):# 我是个函数print("我是三函数")c(4, 5, 6)
print(c.__name__)
print(c.__doc__)运行一下:

这时我们发现我要的是c函数,但给我反馈的是inner函数,这是为什么呢?
这就是工作原理,直接就把c函数装饰成了inner函数,那以后再工作中一定会要自己函数的名字,而不要我装饰后的函数,这样就可以让我们的函数装饰的更像,其实在以后中,都想装饰的更像,那我们应该怎末办?
这时就需要我们的第三方模块functools,直接上代码
import functoolsdef outer(origin):@functools.wraps(origin)def inner(*args, **kwargs):# 我是一个装饰器函数print("装饰器的学习")res = origin(*args, **kwargs)print("装饰器的学习")return resreturn inner@outer
def c(a5, a6, a7):# 我是个函数print("我是三函数")c(4, 5, 6)
print(c.__name__)
print(c.__doc__)这时再运行一下
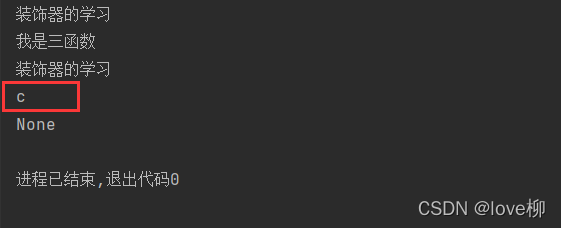
这时我们发现,我们伪装成功了,这样就会让我们的装饰更像。
-
装饰器模板:
接下来送给大家装饰器的模板,以后需要随时ctrl+c和ctrl+v
import functoolsdef outer(origin):@functools.wraps(origin)def inner(*args, **kwargs):# 这里书写需要装饰的功能res = origin(*args, **kwargs)return resreturn inner记得要在需要装饰的函数前要写上@outer哦
总结:
综上,就是关于装饰器的所有知识点,希望大家能学到,最后希望大家多提宝贵意见,我们下期见。