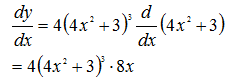优化问题(即高数中的求极值)可分为三类:无约束、等式约束、不等式约束。
对于无约束的优化问题:求导,令导数为零即可求解。
等式约束优化:(拉格朗日乘子法最开始就是求解等式约束优化的方法)
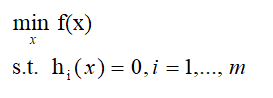
利用拉格朗日函数:

再对其求导

由此将有等式约束的原函数变成无约束的拉格朗日函数进行求解。
那么为什么拉格朗日乘子法可以这样用呢!
举个例子:


红色箭头和蓝色箭头会在满足条件的极值点共线,根据向量共线也能写出下式

故拉格朗日函数其实只是将这个计算过程变成了一个新的函数求一阶偏导的过程,而将原函数变成新函数则借助了拉格朗日乘子,在等式中只要求拉格朗日乘子不为0。

对于多个不等式约束,朗格朗日乘子法仍然适用。
图中蓝线和黑线表示两个等式约束。

不等式约束的优化(广义拉格朗日函数用于求解此类问题)
假设有一个不等式约束条件:
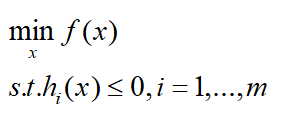
定义广义拉格朗日函数为:

需要满足的KKT条件:

满足KKT条件后极小化广义拉格朗日函数即可得到在不等式约束条件下的可行解。那么在拉格朗日函数中求可行解的过程中就运用到了拉格朗日的一个重要结论——对偶问题。对于这个结论的证明我将放在广义拉格朗日证明的后面。
下面我们先来理解为什么不等式约束优化的朗格朗日函数除了求导还有其他的KKT条件。
还是刚才的例子,只不过约束条件变成了不等式:
首先我们要知道:不是所有的不等式约束都有效,如下图所示:

对于可行域的点我们可以分成两类:边界点及内点
边界点当然就是h=0,此时我们还需要明白f的梯度与约束条件的梯度方向是始终相反的。

原因如下:在 g(x)≤0 一侧,而 g(x)的梯度是指向大于 0 的一侧,也就是不是可行域的一侧。而求的问题是极小值,所以 f(x)在交点处的梯度是指向可行域的一侧,也就是说两个梯度一定是相反的,故有 ,>0.
而对于内点来讲,其实就相当于没有这个等式约束。即只需要对f(x)求导即可,故此时 =0.
将上述两种情况结合到一起就有:

补充一个小tip:
约束条件和拉格朗日乘子互补松弛,即当约束条件松弛时(h<0),拉格朗日乘子紧( =0);反之也如此。

好啦,到现在我们已经明白这些条件是怎么来的了。
下面我们来看看拉格朗日函数的对偶问题: