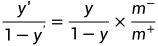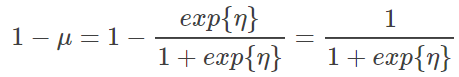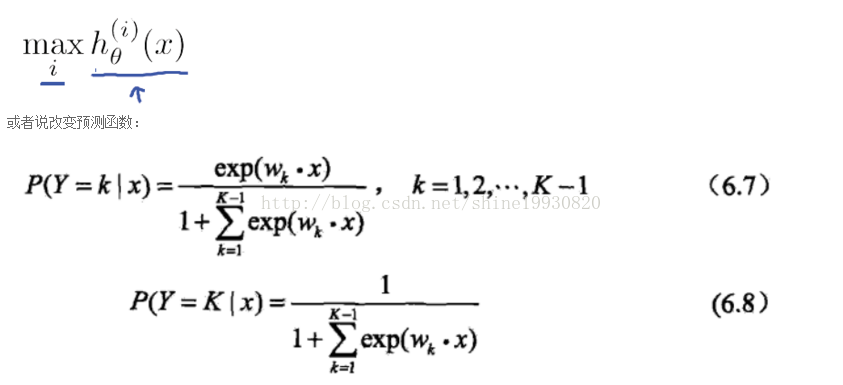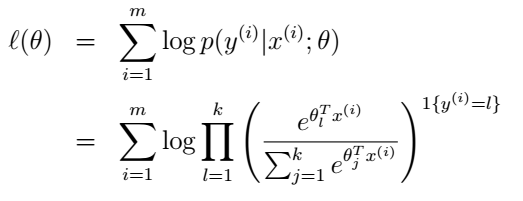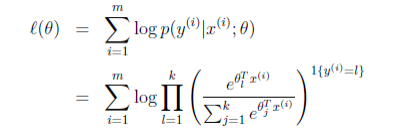线性模型（linear model）
线性模型试图学得一个通过属性的线性组合来进行预测的函数，即：
...
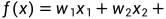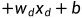(其中
;...;
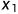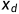为输入属性，
;...;
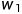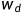和b为模型参数)
向量表示为：
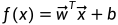(其中
为输入属性向量，
和b为模型参数)
线性模型的优点：
1.形式简单、易于建模
2.通过引入层级结构或高维映射可得到非线性模型
3.具有很好的可解释性（直观表达了各属性在预测中的重要性）
线性回归
1.单变量线性回归
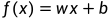
2.多变量线性回归（多元线性回归）
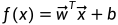
线性回归试图学得一个线性模型以尽可能准确地预测实值输出标记。
常使用均方误差作为性能度量，试图让均方误差最小化。基于均方误差最小化来进行模型参数求解的方法称为“最小二乘法”
线性回归任务使用最小二乘法来进行参数估计，获得w和b的值。
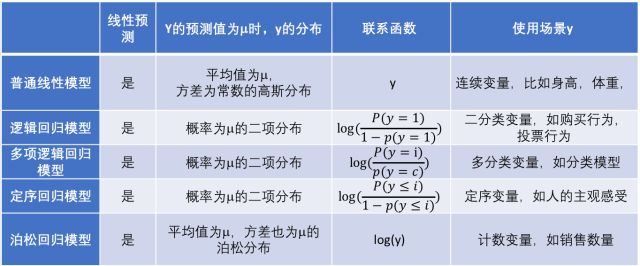
广义线性模型（general linear model）
当模型的预测值逼近真实标记y时，就得到了线性回归模型。
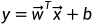
当模型的预测值逼近y的衍生物时，如逼近标记y的对数即lny时，线性回归任务变成了“对数线性回归”，其形式上仍是线性回归，但实质上已经是在求取输入空间到输出空间的非线性函数映射。对数函数起到了将线性回归模型的预测值与真实标记联系起来的作用。此时，得到的模型可以称为广义线性模型，其中的函数称为联系函数。
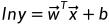
联系函数为g(·)可推广为：
对数几率回归
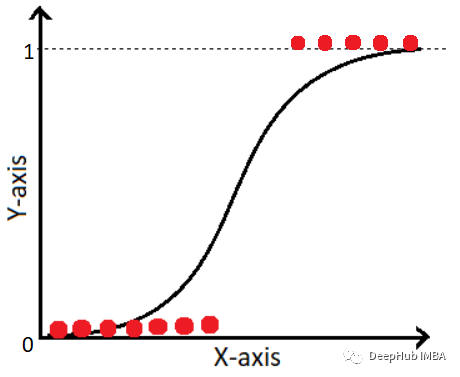
把对数几率函数（sigmoid函数）作为联系函数，将预测实值z转换为0/1值。所得数值为正例可能性，可能性大于0.5则判定为正例1，小于0.5则判定为反例0。
对率函数及图像：
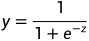
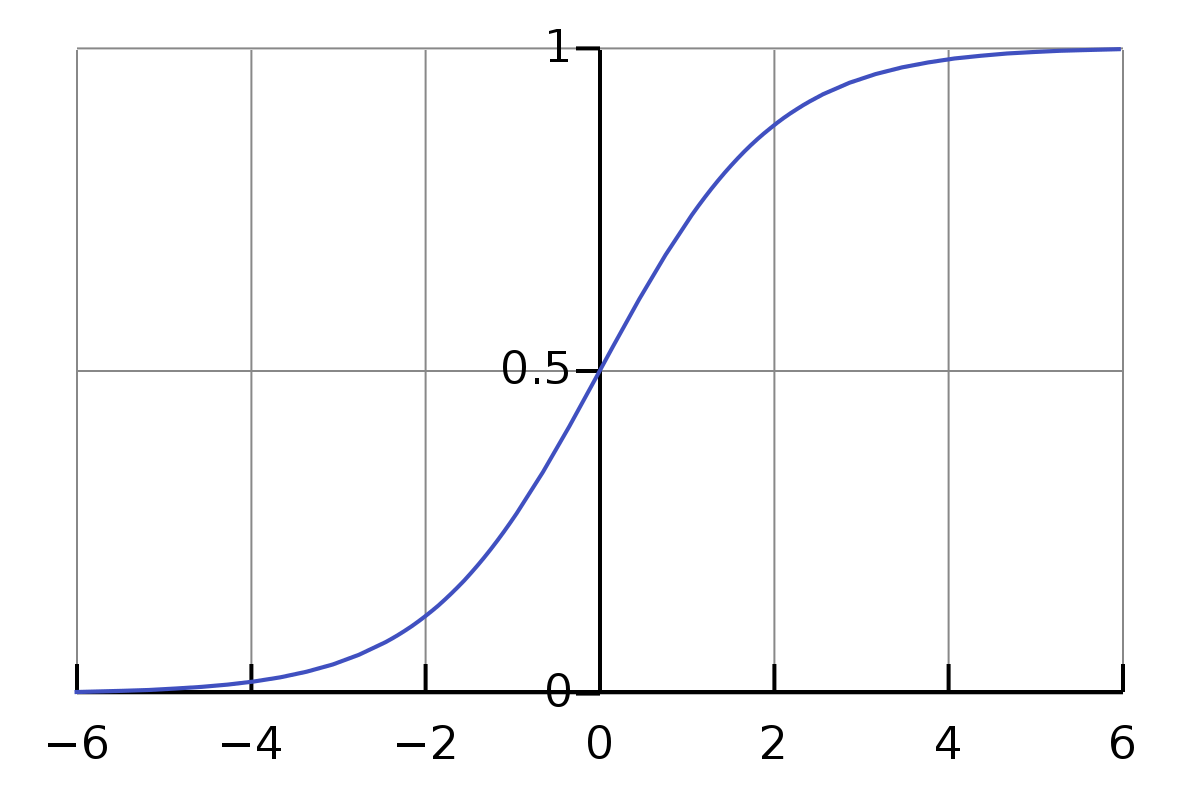
其中z为模型预测实值，将z代入可得：
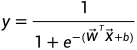
可变化为：
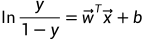
将y视为样本正例的可能性，则1-y为样本反例可能性，两者比值称为“几率”，反映了x作为正例的相对可能性:
对几率取对数则得到“对数几率”:
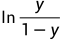
该方法对应的模型称为“对数几率回归”，名字是“回归”，但实际是一种二分类学习方法。
二分类任务使用极大似然法进行参数估计
多分类任务
可通过拆解法，将多分类任务拆为若干个二分类任务。通常有三种拆分策略：
One vs One:将N个分类两两配对，从而产生N(N-1)/2个二分类任务。在测试阶段，新样本将同时提交给所有分类器，于是将得到N(N-1)/2个分类结果，最终结果可通过投票产生：即把被预测得最多的类别作为最终分类结果。
One vs Rest：将一个类的样例作为正例、所有其他类的样例作为反例来训练N个分类器。在测试阶段，仅有一个分类器预测为正类，则对应的类别标记作为最终分类结果。
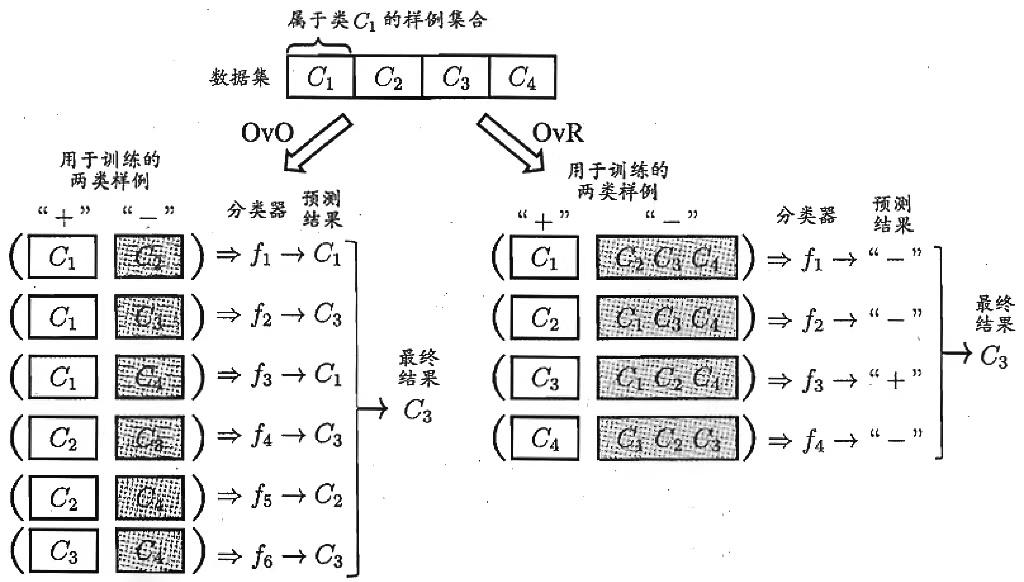
Many vs Many：每次将若干类作为正例，若干个其他类作为反例。
容易看出，OvR只需要训练N个分类器，而OvO需训练N(N-1)/2个分类器，因此，OvO的存储开销和测试时间开销通常比OvR更大。但在训练时，OvR的每个分类器均使用全部训练样例，而OvO的每个分类器仅用到两个类的样例，因此，在类别很多的时候，OvO的训练时间开销通常比OvR更小。
类别不平衡问题
如果不同类别的训练样例数稍有差别，通常影响不大，但若差别很大，则会对学习过程造成困扰。例如有998个反例，但正例只有2个，那么学习方法只需返回一个永远将新样本预测为反例的学习机器，就能达到99.8%的精度。然而这样的学习器没有什么价值，因为它不能预测出任何正例。
类别不平衡就是指分类任务中不同类别的训练样例数目差别很大的情况。在现实的分类学习任务中，经常会遇到类别不均衡，例如在通过拆分法解决多分类问题时，即使原始问题中不同类别的训练样例数目相当，在使用OvR、MvM策略后产生的二分类任务仍可能出现类别不平衡现象。
从分类器的角度讨论，在使用线性模型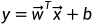对新样本x进行分类时，事实上是在用预测出的y值与一个阈值进行比较，例如通常在y>0.5时判别为正例，否则为反例。y实际上表达了正例的可能性，几率则反映了正例可能性与反例可能性之间的比值，阈值设置为0.5恰表明分类器认为真实正、反例可能性相同，即分类器决策规则为：
若 > 1则预测为正例
然而，当训练集中正、反例的数目不同时，令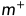
表示正例数目，
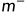表示反例数目，则观测几率是
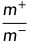，由于通常假设训练集是真实样本总体的无偏采样，因此观测几率就代表了真实几率。于是，只要分类器的预测几率高于观测几率就应判为正例，即分类器决策规则为：
若 > 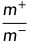则预测为正例
但是，分类器实际是基于第一个规则决策的，因此，需要对其预测值进行调整，使其决策规则向第二个靠拢，这就是类别不平衡学习的一个基本策略“再缩放”。可令：
